Матрица весов примера

Таблица 10.1

В соответствии с теоремой 2 добавим к каждому элементу, стоящему либо в строках 8 и 9, либо в столбцах 8 и 9 таблицы 10.1, достаточно большое число к (скажем, 1000). Получившуюся после этого добавления таблицу назовем результирующей матрицей весов С.

Далее поступаем следующим образом.

Находим кратчайший остов графа G. Если он окажется гамильтоновой цепью, то задача решена. В рассматриваемом примере кратчайший остов, показанный на рис. 10.12 (а), не является гамильтоновой цепью. Степени вершин 1 и 7 равны 4, а не 2, как это требуется для гамильтоновой цепи. Следуя духу теоремы 3, мы можем оштрафовать эти вершины. Допустим, что мы произвольно выбрали малый шаг (скажем, 5 единиц), так что все штрафы кратны ему. (Можно выбрать величину шага равной 1, но это будет неоправдано мало и приведет к увеличению числа требуемых итераций.) Таким образом, если мы решили штрафовать только те вершины, степени которых больше чем 2, то

p(0 = 5(df-2).

(10.13)

Заметим, что метод штрафования вершин выбран произвольно и существует много других альтернатив (см. разд. 6.3.4).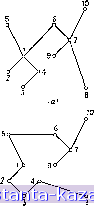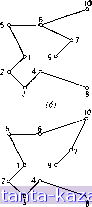

Рис. 10.12. Кратчайшие остовы при итерациях со штрафами.

В соответствии с уравнением (10.13) штрафы вершин 1 и 7 равны ]э (1) = ]э (7) = 10, причем для всех остальных вершин онн равны 0. Следуя (10.11), вычислим новую матрицу весов и найдем для нее кратчайший остов. Результат показан на рис. 10.12 (б), из которого видно, что это дерево много ближе к гамильтоновой цепи, поскольку для него g = 1 вместо е = = 4 в предыдуш,ем случае.

Поступая как и ранее, оштрафуем вершину 6 и положим р (6) = = 5. (Следует заметить, что этот новый штраф добавляется к предыдущей матрице весов, а не к первоначальной матрице С.) Таким образом, штрафы равны тр {\) ~ тр (7) = 10, ]э (6) = 5 и ]э (i) = О для всех остальных вершин. Соответствующий кратчайший остов изображен на рис. 10.12 (в), и для него е = 1, как и для предыдущего остова. Оштрафуем вершину 7, полагая р (7) = 5; новый кратчайший остов будет тем же, что и на рис. 10.12 (б). Продолжая далее, штрафуем вершину 6 еще раз, полагая р (6) = 5, и опять находим кратчайший остов. Результат показан на рис. 10.12 (г), из которого видно, что теперь это гамильтонова цепь и, следовательно, по теореме 3 - кратчайшая гамильтонова цепь. Вес этой цепи с первоначальной матрицей весов Сц равен 258.

Здесь полезно отметить, что если на некотором этапе получается кратчайший остов, уже встречавшийся ранее, то это не означает, что произошло зацикливание, и любой такой цикл автоматически устраняется при продолжении алгоритма. (Однако, как будет выяснено ниже, сходимость последовательности кратчайших остовов к кратчайшей гамильтоновой цепи не может быть гарантирована без конкретизации выбираемого способа штрафования вершин.) Мы получили кратчайшую гамильтонову цепь с концевыми вершинами 8 и 9 за 5 итераций, включая 5 вычислений кратчайших остовов, в то время как полный перебор содержал бы 8! = 40320 вычислений матриц весов и сравнений цепей.

Альтернативой к вышеописанному методу штрафов является следующий. Вместо штрафования только тех вершин, для которых

> 2 (с использованием (10.13)), можно штрафовать только те вершины (за исключением двух выделенных конечных вершин), степени которых df = 1 <i2, причем величина штрафа р {i) отрицательна и равна выбранной единице шага. С другой стороны, можно применить комбинацию этих двух политик наложения штрафов или воспользоваться совершенно другими политиками, описанными в разд. 6.3.4. Здесь следует отметить, что выбор политики наложения штрафов может существенно влиять на число необходимых для получения решения итераций.

Предположим в качестве примера, что на втором этапе описанных вычислений - когда кратчайший остов изображен на рис. 10.12 (б) - мы репшли воспользоваться второй политикой наложения штрафов и вместо того, чтобы положить р (6) = 5, взяли р (10) = -5. Получившийся кратчайший остов был бы таким, какой показан на рис. 10.12 (г), т. е. он немедленно дал бы кратчайшую гамильтонову цепь.

Интересно отметить, что не существует единственного вектора штрафов р (г), г = 1, . . ., и, для которого матрица весов будет преобразовываться так, что кратчайпшй остов будет и гамильтоновой цепью и, следовательно, кратчайшей такой цепью. В приведенном примере окончательное значение вектора штрафов при первой политике такое: р {i) = р (6) = 10, р (7) = 15, все остальные р (О = 0; в то же время при второй политике, принятой, начиная с шага 2, для окончательного вектора штрафов р (1) = - Р О) = 10, J3(10) = - 5, все остальные р (i) - 0.

6.3.2. Решение задачи (а). Мы проиллюстрировали сначала применение алгоритма штрафования верпшн к задаче (б), так как к этой задаче непосредственно применима теорема 3. Подобно тому как для решения задачи (б) с помощью алгоритма поиска, использующего дерево решений, она была сведена к задаче (а), так и сейчас, чтобы решить задачу (а) с помощью алгоритма