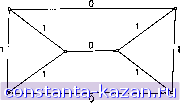Рис. 10.13.

[7] и, в несколько иной форме, примерно в то же время Хелдом и Карпом [18]. Последние авторы показали также, что итерационный метод не обязательно сходится, и в качестве подходящего примера предложили граф, изображенный на рис. 10.13. Несмотря на этот большой недостаток, метод является тем не менее очень ценным по двум причинам.

Во-первых, в большинстве случаев он сходится (как будет показано ниже, все 33 случайно выбранные задачи были решены

штрафования вершин, мы сведем ее к задаче (б). Это осуществляется посредством следующего приема.

К множеству X вершин графа G добавим еще две вершины, например и х^, и образуем новое множество X = X [} {xi, х^}. К множеству ребер А графа G добавим два множества ребер:

Si=\J{{xuj)} и S=l}{{x2,xj)}, j=i j=i

и образуем новое множество А' = А [J i U г- Для всех / = = 1, . . ., ге зададим веса а - для ребер (xi, Xj) и b - для ребер (2, Xj), где а ж b - две произвольные постоянные.

Теорема 4. Решение задачи (б) для графа G = (X, А') с концевыми вершинами х^ и х^ является решением задачи (а) для графа G.

Доказательство. Любая гамильтонова цепь графа G с концевыми вершинами х^ и х^ может рассматриваться как гамильтонова цепь, проходящая через вершины графа G с добавленными ребрами {хх, а:,) и {х^, Xj), Xi, Xj 6 X. Таким образом, вес гамильтоновой цепи ИЗ G равен, скажем, F = F а Ь, где F - вес некоторой гамильтоновой цепи из G, и, следовательно, вес F минимален только тогда, когда F минимален, т. е. когда F соответствует кратчайшей гамильтоновой цепи из G. Теорема доказана.

6.3.3. Сходимость метода штрафования вершин. Метод штрафования вершин, описанный выше, был развит Кристофидесом

ЭТИМ методом по крайней мере при одной стратегии наложения штрафов).

Во-вторых, допустим, ЧТО итерации остановлены в некоторый момент, когда кратчайший остов с модифицированной матрицей есть 7 , штрафы вершин р (t), t = 1, 2, . . ., п, и степени вершин d\; рассматриваем задачу, когда нужно найти кратчайшую гамильтонову цепь с концевыми вершинами и Xj. Вес остова Т' с модифицированной матрицей равен

Ft-Ft-+ S P(i)dT + р{\)+р{2),

гф1, 2

где Fj. - вес остова 7 , вычисленный для первоначальной матрицы весов.

Если Н - кратчайшая гамильтонова цепь графа, то вес цепи Н с модифицированной матрицей равен

Fh = h + 2 S P(i)+P(l) + P(2).

Так как по определению Fx- <.Fjj, то разность

/(p)Fh-Ft- = Fh-[Ft4- S p{i){dT-2)\ (10.14)

il. 2

является мерой близости дерева Т' к кратчайшей гамильтоновой цепи я, причем / (р) =0, если Т' = Н.

Величину / (р) МОЖНО рассматривать как функцию вектора штрафов p = (pji = l,..., п). Хелд и Карп предложили два метода нахождения штрафов р*, минимизирующих / (р). Один основан на технике преобразования столбцов, а второй является методом наискорейшего спуска. (Другой, несколько более общий последовательный подход, основанный на эвристическом поиске, был недавно успешно применен Камерини и др. [4].) Если метод штрафования вершин сходится, то для минимального значения / (Р*) = О' так как Г' я и =2 для всех t 1, 2. С другой стороны, как было отмечено выше, метод сходится не всегда, и при отсутствии СХОДИМОСТИ минимальное значение / (р*) величины / (р) равно некоторому положительному числу. Совершенно очевидно, что в этом случае величина

Ft+ S p*(i)idr-2) (10.15)

гф1, 2

дает нижнюю границу веса кратчайшей гамильтоновой цепи. В этом последнем случае получаемая граница является очень точной и может быть использована с большим эффектом [19] в алгоритме поиска, применяющем дерево решений,- в духе того, как это делалось в разд. 6.2.1.

6,3.4. Стратегии наложения штрафов. Хотя, как уже отмечалось в разд. 6.3.3, существуют два метода [18] для определения последовательности штрафов, вынуждающих кратчайший остов становиться кратчайшей гамильтоновой цепью (если только вообще сходимость возможна), оба эти метода являются слишком изысканными и требуют больших затрат времени. В настоящем разделе мы экспериментально исследуем влияние различных стратегий штрафования вершин на скорость сходимости метода. Для всех 33 случайно выбранных полных графов, использованных для проверки стратегий, по крайней мере одна стратегия приводила к кратчайшей гамильтоновой цепи. Это убеждает нас в том, что, хотя и существуют задачи, в которых алгоритм штрафования вершин не сходится (на самом деле любой связный граф без гамильтонова цикла приводит нас к такой ситуации), но все же в большинстве задач, при составлении которых не старались специально найти контрпримеры, будет иметь место сходимость.

(I) Фиксированные штрафы

(a) Только положительные штрафы

Это тот случай, когда все вершины Xi дерева Т со степенями > 2 штрафуются на величину y-idj - 2), а все остальные вершины не штрафуются. Было найдено, что для малых у число необходимых для достижения решения итераций (т. е. определения некоторого гамильтонова цикла) приблизительно обратно пропорционально величине у, но для достаточно больших у вполне возможно зацикливание и решение получено не будет. Наилучшее значение у зависит как от числа вершин, так и от распределения весов ребер.

(b) Только отрицательные штрафы

Это тот случай, когда вершины (за исключением двух отмеченных концевых вершин) штрафуются на величину - у, если а остальные не штрафуются. Результаты примерно те же, что и в случае (а).

(c) Положительные и отрицательные штрафы

В этом случае вершины штрафуются в соответствии с (а) и (Ь), в зависимости от того, будет ли df > 2 или d{ = i соответственно. Было найдено, что значение у, равное половине используемого в случаях (а) и (Ь), обеспечивает сходимость примерно эа то же самое число итераций, что и в случаях (а) и (Ь). Этот метод в общем лучше методов (а) и (Ь).