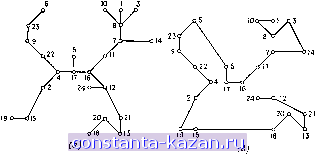Рис. 10.14. Задача с 24 вершинами, (а) Начальный кратчайший остов, (б) Кратчайший гамильтонов цикл, полученный после 40 итераций с использованием штрафов 111(c).

наименьшего веса в цепи от к Xj), то степень вершины Xi станет равной 2 после единственной итерации.

Если все штрафы р (г) накладываются одновременно, то, как и в случае (III (а)), взаимодействие этих штрафов делает невозможным предсказание изменения степеней вершин после одной итерации.

(с) Положительные и отрицательные штрафы Эта стратегия заключается в наложении штрафов на вершины в соответствии с (III (а)) или (III (Ь)) в зависимости от того, будет ли > 2 или dJ = 1.

В таблице 10.2 приводятся результаты и делается сравнение семи стратегий штрафования, описанных выше. Графы в этой таблице были получены случайным выбором п точек в квадрате при равномерном распределении, а в качестве весов ребер Cij бралось евклидово расстояние между i и /. Таблица дает числа итераций и времена вычислений (ЭВМ СВС 6600, время в секундах), необходимые для получения ответа. Из этой таблицы видно, что действие всех стратегий штрафования зависит от задачи, хотя можно заметить, что наилучшей является стратегия (III (с)). Используя эту стратегию, можно найти кратчайшую гамильтонову цепь в графе примерно с 60 вершинами менее чем за 15 с.

На рис. 10.14 для некоторого графа с 24 вершинами показаны начальный кратчайший остов и окончательная кратчайшая гамильтонова цепь. Первая и последняя пронумерованные вершины являются отмеченными концевыми вершинами.

6.4. Задачи, родственные задаче коммивояжера

До сих пор в разд. 6 мы имели дело с открытой задачей коммивояжера, т. е. с кратчайшей гамильтоновой цепью (а не с циклом). Вначале это было оправдано тем, что при этом мы имеЛи дело с более прямой связью открытой задачи с кратчайшим остовом. С другой стороны, нужно сделать только очень небольшие изменения, чтобы подойти и к замкнутой задаче коммивояжера. Хелд и Карп [18], например, ввели понятие кратчайшего 1-дерева графа G, причем оно определяется как кратчайший остов порожденного подграфа графа G с удаленной вершиной 1 плюс два кратчайших ребра, исходяш;их из вершины 1 к двум другим вершинам дерева. Очевидно, что между понятием кратчайшего 1-дерева и замкнутой задачей коммивояжера суш;ествует та же самая связь, что и между понятием кратчайшего остова и открытой задачей. Таким образом, штрафование вершин изменяет относительные веса 1-деревьев, но оставляет инвариантным относительное упорядочение гамильтоновых циклов. Так же совершенно очевидно, что, как в открытой задаче, кратчайший остов со всеми вершинами степени 2 (за исключением двух концевых вершин) становится кратчайшей гамильтоновой цепью между этими концевыми вершинами, так и в замкнутой задаче кратчайшее 1-дерево, все вершины которого имеют степень 2, является кратчайшим гамильтоновым циклом графа. Алгоритм штрафования вершин, обсуждавшийся ранее в данном разделе, может быть использован поэтому фактически без изменений и для решения замкнутой задачи коммивояжера.

7. Задача коммивояжера и задача о назначениях

В разд. 5 было отмечено, что задача о назначениях, определяемая соотношениями (10.4), (10.5) и (10.6), может иметь решения, образованные некоторым числом непересекаюш;ихся циклов, и что соответствуют;ий метод решения задачи коммивояжера требует наложения ограничений до тех пор, пока решение не будет состоять из единственного (гамильтонова) цикла. В настоящем разделе мы исследуем процедуры наложения этих ограничений в рамках алгоритма поиска, использующего дерево решений. Применяемая схема будет в основном такой же, как и в разд. 6.2 для алгоритма поиска, основанного на рассмотрении кратчайшего остова.

О

Рис. 10.15. Решение задач о назначениях, (а) Решение задачи Pq. (б) Решение задачи Р^.

сделать следующее - исключить данное решение вместе со многими другими такими же решениями, не потеряв решение задачи коммивояжера с той же матрицей весов. Так как решение задачи коммивояжера является гамильтоновым циклом, то мы будем пытаться исключить любое решение, состоящее более чем из одного цикла.

(А) Правило простого ветвления. Пусть в общем случае решение задачи о назначениях содержит (не гамильтонов) цикл (xj, 2, . . ., Xft, Xi) длины к. Удаление этого цикла (и всех решений, его содержащих) из дальнейшего рассмотрения может быть произведено путем наложения требования, что но крайней мере одна из дуг (xi, Х2), {х2, Хз), . . ., (xft, Xi) не должна входить в решение. Это можно сделать совсем просто, если первоначальную задачу с матрицей весов Icij] разбить на к подзадач Pi, Р2, . . . , Р^-В задаче Pi c{xi, Х2) полагается равным оо, а все остальные Ctj остаются без изменения (т. е. такими же, как и в задаче Ро), в задаче Р2 с {х2, Хз) = оо и вообще в задаче Р^ с (х^, Xj) = 00. Очевидно, что решение задачи Р^, не содержащее цикла (xi, Xj, . .

Xft, Xj), является решением по крайней мере одной из задач Pi,. . . . ., Pft и, следовательно, оптимальное решение задачи коммивоя жера является решением одной или нескольких из этих подзадач

Так, например, исключая на рис. 10.15 (а) цикл длины 3 получим дерево решений, изображенное на рис. 10.16, в котором задачи Pi, Р^ ж Pg представлены узлами дерева, растущего из начальной задачи Р^. Пусть задачи Pi, Р2 и Р3 решены как задачи о назначениях, и пусть соответствующие веса будут Ci, С2 и Cg. Так как Ci является нижней границей в задаче коммивояжера

7.1. Алгоритм поиска, использующий дерево решений

Пусть решение задачи о назначениях с матрицей весов [cij] где с и = оо, V0 образовано некоторым числом непересекающихся циклов. Так, например, если решение задачи с 8 вершинами имеет вид = Еге = 1з5 = 1*7 = 54 = ?6i = Its = Iss = 1

и = О для всех остальных нар (г, /), то решение, отвечающее двум циклам, изображено на рис. 10.15 (а). Теперь необходимо