ДЛЯ Pi, а также для Р^, и Р^, то число L = min (Ci, С^, С^) является нижней границей для веса решения первоначальной задачи коммивояжера.

Пусть, скажем, L = Ci (т. е. С^С^ и CiCg). Если решение задачи Pi является гамильтоновым циклом, то оно будет решением первоначальной задачи коммивояжера. В противном случае пусть оно будет, скажем, таким, как на рис. 10.15 (б). Исключая цикл (1, 8, 2, 6, 1), мы снова составляем и решаем подзадачи Р^, Р^, Рв и Р^, показанные на рис. 10.16. Из этого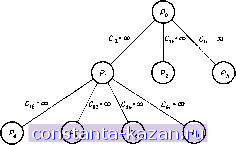

Рис- 10.16. Дерево решений с простым правилом ветвления А.

рисунка видно, чю Р^ отвечает задаче, для которой в матрице весов элемент положен равным со (в дополнение к тому, что элемент положен равным со уже ранее). То же самое относится и к Р^, Р^ и Рт. Нижняя граница теперь переопределяется как L = min (Сг, Сз, С^, С^, Cg, Cj). Допустим, что задача Рз соответствует весу L (т. е. L = Сз). Если решение задачи Рз является гамильтоновым циклом, то оно будет решением первоначальной задачи коммивояжера. Дальнейшее ветвление в узле Рз, с другой стороны, должно осуш;ествляться точно так же, как это делалось в Pi, ж этот процесс продолжается до тех пор, пока задача с теку-щ;им значением веса L не будет иметь в качестве решения гамильтонов цикл. Когда это произойдет, то полученный цикл будет окончательным решением, так как его вес (по определению числа L) не превосходит нижних границ весов любых других гамильтоновых циклов, которые могут появиться при дальнейшем ветвлении в оставшихся узлах дерева.

Из приведенного описания алгоритма становится очевидным, что примененный поиск с помош;ью дерева решений относится к типу с приоритетом по ширине , как это объяснено в приложении 1.

(Б) Правило исключающего ветвления. Как объяснено в приложении 1, для хорошего ветвления при разбиении задачи Ро на подзадачи Pi, Р^ и Р3 требуется только, чтобы каждое возможное решение задачи Ро (за исключением удаляемых решений) было решением по крайней мере одной из подзадач. Однако, как отмечено в приложении, очень желательным свойством метода ветвления было бы разбиение возникающих подзадач на взаимно исключающие, коль скоро речь идет о возможных решениях задачи Ро. Иными словами, каждое допустимое решение задачи Р^ должно быть решением одной, и только одной из этих подзадач.

Ранее описанное правило ветвления основывалось на том факте, что цикл, такой, как (xi, х^, . . ., х^, Xi), может быть удален посредством исключения одной из его дуг. Это, однако, не приводит в процессе ветвления к взаимно исключающим подзадачам. Так, в вышеприведенном примере решение задачи Ро, соответствующее циклам (1, 3, 6, 1) и (2, 5, 4, 7, 8, 2), является допустимым решением как подзадачи Pi (с Cjg = 00), так и (с Cgg = 00).

Другим правилом ветвления, удаляющим цикл {xi, х^, . . . . ., Хи, Xi) ж приводящим к взаимно исключающим подзадачам, является следующее:

для задачи Р^ положить с {xi, х^) = оо;

для задачи Р^ положить с {xi, х^) - - М ж с {х^, Xg) = оо;

для задачи Р^ положить с [xi, х^) = с {х^, Xg) = - М ж с [хз, Xi) = 00.

для задачи Р^ положить с (xj, х^ = с {х^, Xg) = ... = = с (Xft i, хи) - М же (Хй, Xi) = 00,

где -М - достаточно большое отрицательное число, гарантирующее, что дуга, вес которой равен -М, входит в оптимальное решение.

Это правило ветвления наверняка приводит к взаимно исключающим подзадачам, так как для любых двух подзадач имеется по крайней мере одна дуга, исключенная из решения одной, но заведомо входящая в решение другой подзадачи. Легко также видеть, что ни одно возможное решение задачи Ро не будет потеряно, т. е. что любое решение первоначальной задачи Ро будет являться решением одной из подзадач. Это очевидно в силу того, что любое решение задачи Ро имеет некоторую последовательность дуг, выходящую из xi, таких, как (х^, х ), (х^, хр) и т. д., и первые г дуг должны совпадать с дугами цепи (х^, Xg, Xg, . . ., х^) при некотором значении г = 0, 1,..., к. Значение г = О отвечает тому случаю, когда совпадения вообще нет, г = 1 - случаю, когда Хсс = Ха, но Х^ф Хз ж т. д.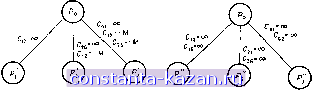

Рис. 10.17. Дерево решений с исклю- Рис. 10.18. Дерево решений с улуч-чающим правилом ветвления Б. шейным правилом ветвления В.

В приведенном примере первоначальная задача Ро разбивалась бы на три подзадачи, показанные на рис. 10.17 (ср. с разбиением на первом уровне из рис. 10.16, полученным по предыдущему правилу ветвления).

(В) Лучшее правило ветвления. Оба предыдущих правила ветвления исключали (при каждом отдельном ветвлении) все решения, содержащие заданный цикл, такой, как {xi, х^, . ., х^, Xi). Очевидно, однако, что в решении задачи коммивояжера не только не должен не существовать такой цикл, но должна быть по крайней мере одна дуга, ведущая из множества вершин S = {х^, . . . . . ., Xfi} в множество вершин S = X - S. Действительно, существование какой-либо дуги, ведущей из 5 в 5, не только гарантирует исключение решений, содержащих цикл, принадлежащий множеству S, но также позволяет исключить решения, множества вершин которых лежат в 5 и которые состоят из нескольких циклов (а не только из одного). Таким образом, можно ожидать, что правило ветвления, основанное на требовании, чтобы существовала некоторая дуга шз S в S, будет равномерно лучше, чем два предыдущие правила ветвления 2.

Так как дуга шз S в S должна начинаться в некоторой вершине из S, то задачу можно расщепить на к подзадач. В подзадаче Pj мы будем требовать, чтобы начальной вершиной дуги являлась Xi 5, а конечной вершиной была некоторая вершина в S. Это можно сделать, положив с (х xj) = сю для всех xt S ш оставив без изменения все другие веса. В решении получившейся задачи о назначениях мы наверняка бы имели дугу из Xi, ведущую в S, так как для всех других альтернатив их веса должны быть положены равными сю.

В примере, данном выше, начальная задача Рд была бы в соответствии с настоящим правилом ветвления подразделена на три подзадачи, определенные, как показано на рис. 10.18. Дальнейшие ветвления происходят аналогично.