В задачах, графы которых содержат такие скопления вершин, что дуги в одном и том же скоплении имеют малые веса, а дуги между вершинами из разных скоплений имеют большие веса.)

Тем не менее вышеописанный алгоритм работает не слишком хорошо в симметричных задачах, так как в них решения задач о назначениях обычно состоят из большого числа циклов длины 2 и для их исключения требуется очень много ветвлений. Еще хуже обстоит дело тогда, когда задача коммивояжера решается на графе, который не содержит гамильтоновых циклов конечного веса.

7.4. Лучшие границы для дерева поиска

Мы оппсали в разд. 7.1 алгоритм поиска, в котором в качестве нижней границы в узле берется значение из решения соответствующей задачи о назначениях. На самом-то деле совершенно очевидно, что метод исключения циклов остается неизменным независимо от того, какая нижняя граница используется для ограничения поиска. Но так как процесс ветвления в узле прекращается только тогда, когда или решение подзадачи, отвечающей этому узлу, является гамильтоновым циклом, или когда нижняя граница в узле превосходит значение полученного до этого наилучшего решения, то очевидно, что качество оценки границы оказывает заметное влияние на число ветвлений в дереве решений п, следовательно, на вычислительную эффективность метода. Целью настоящего раздела является описание метода получения нижней границы, вычисляемой по решению задачи о назначениях с небольшими дополнительными усилиями и являющейся более точной, чем ранее используемые границы. Пусть решение задачи о назначениях содержит некоторое число циклов, как это показано в качестве примера на рис. 10.20 (а). Пусть г-й цикл обозначается Si, и пусть число циклов равно щ. (Мы будем использовать один и тот же символ Si, как для обозначения цикла, так и для обозначения множества его вершин.)

Определим стягивание как замену цикла единственной вершиной. Полученный граф содержит rii вершин Si,i (t = 1, 2, . . . . . ., щ). В качестве матрицы весов нового графа берется (щ X X 7г1)-матрица Ci = [ci {Si,i, Sij)] с элементами вида

Ci{Si.t,Si,j)= min [hiki,kj)], (10.19)

где Fl ~ Ifi {к{, kj] - окончательная матрица относительных весов, полученная в конце решения задачи венгерским (например) методом (см. гл. 12).

Первое стягивание

Второе стягивание

Третье стягивание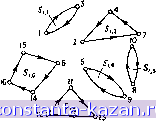

5 / 3.,

Рис. 10.20. Процесс стягивания. Первое стягивание, второе стягивание, третье стягивание.

На рис. 10.20 (а), например,

ci(5i,5,5i.6)= min [fiik k,)].

Лб6{И, 12, 13} He{6, 14, 15, 16}

Теперь второе решение задачи о назначениях в случае задачи с матрицей все еще может содержать циклы, в качестве вершин которых выступают предыдущие циклы. Рис. 10.20 (б) показывает один из возможных способов образования новых циклов 82,1 {i ~ = 1,2,..., 2)1 где 2 - их общее число (на рис. 10.20 (б) щ = = 3). Эти циклы опять могут быть стянуты в вершины и дать новую задачу с новой матрицей весов €2= \с2 {82,1, 82,])], вычисленной так же, как и в (10.19), т. е.

2(2,1,-52, j)= min [f2iki,kj)], (10.20)

es2,

где множества 82,1 являются объединениями всех множеств i, образующих частные циклы, и где F2 = [/2 (j, kj)] - матрица относительных весов, полученная в конце решения второй задачи о назначениях.

Решение задачи о назначениях для нового, дважды стянутого, графа все еще может содержать циклы, и итерационный процесс решения - стягивания можно продолжать до тех пор, пока задача не сведется к единственной вершине.

Определим компрессию как преобразование матрицы, не удовлетворяющей аксиоме треугольника в метрическом пространстве, в матрицу, удовлетворяющую этой аксиоме. Таким образом, для компрессии матрицы нужно заменить каждый элемент тц, для которого

niijmiu + mkj (при некотором к),

элементом min [т^ -1- muj] и продолжать эту замену до тех пор, пока

для всякого к не будут справедливы неравенства m-ij т^ + пг}.

Теорема 5. Сумма значений решений задач о назначениях, полученных во время процесса решение - стягивание - компрессия осуществляемого вплоть до момента, когда стянутая задача будет содержать единственную точку), является точной нижней границей для задачи коммивояжера.

Доказательство. В гл. 12 показано, что элемент (г,/) в матрице относительных весов, полученной в конце решения задачи о назначениях, дает нижнюю границу для дополнительного веса, который Получается из-за включения дуги (г, у) в решение.

Рассмотрим цикл i,;, полученный] в конце решения первой задачи о назначениях. Любой гамильтонов цикл, проходящий