 |
 |
 |
 |
|
Главная -> Гидравлические машины: турбины и насосы 1 2 3 4 5 6 7 8 9 10 11 [ 12 ] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 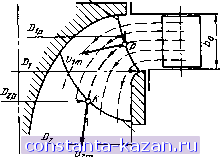 характеристик различных рабочих колес, позволяющих осуществлять построение параллелограммов скоростей. Как наиболее общий случай рассмотрим рабочее колесо радиально-осевой турбины. На меридианное сечение турбины (рис. 3-3) снесены все точки входной кромки лопастей, обозначенные индексом /, и точки выходной кромки, обозначенные индексом 2. Поток, выходящий из направляющего аппарата, разделим на несколько равных по площади и высоте слоев (в данном случае их 6) и траекторию каждого слоя в колесе также снесем на меридианную плоскость. Получим кривые ли-Входная кромка (1) fjjjjj (пунктирные), причем по- верхности вращения каждой такой линии представляют собой поверхности тока, т. е. поверхности, которые не пересекаются движущейся жидкостью (движение представляется слоистым). Таким образом, кривые линии на меридианной плоскости являются сечениями поверхностей тока. Очевидно, чтобы установить полную картину потока в рабочем колесе, нужно рассмотреть течение по всем меридианным поверхностям тока. Но с целью упрощения можно выделить одну, наиболее характерную \ кривую, например среднюю р-k, и по ней проанализировать условия течения. Представим себе сечение лопастей рабочего колеса средней поверхностью тока (кривая pk). Это будут некоторые пространственные формы. Для удобства построений эти сечения сносятся на плоскость, причем сохраняются фактические значения углов (если линия р-k близка к прямой, то это можно осуществить путем развертки конического или цилиндрического сечения, если криволинейна, то отображением). Практическое использование описанного способа будет ясно из дальнейшего рассмотрения конкретных случаев. Сечение рабочего колеса радиальн о-о с е в о й турбины показано на рис. 3-4, а. Здесь Dip и D - расчетные диаметры входной / и выходной 2 кромки лопасти (как видно из рис. 3-3, эти диаметры меньше номинального входного Dj и выходного D). Направление лопастей рабочего колеса в данной точке определяется углом б между касательной к средней линии профиля лопасти, проведенной в сторону течения жидкости, и нормалью к радиусу, проведенной в сторону, обратную вращению колеса. Выходная кромка.(г) Рис. 3-3. Меридианный поток в радиально-осевой турбине. Условия работы турбины (режим) задаются двумя параметрами: расходом Q и частотой вращения п рабочего колеса. При заданных размерах рабочего колеса это дает возможность определить компоненты параллелограммов скоростей. Переносная окружная скорость и выражается формулой 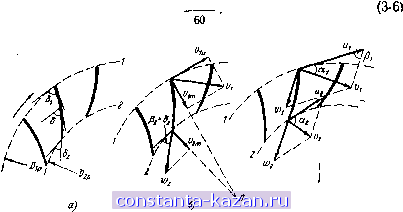 N / в) \ /Л Рис. 3-4. Построение параллелограммов и треугольников скоростей в рабочем колесе радиальио-осевой турбины. Проекция вектора абсолютной скорости на меридианную плоскость - меридианная составляющая w (на рнс. 3-3 показаны Vi и приближенно может быть найденй из соотношения v.-, (3-7) Рде - суммарная площадь потока в колесе, нормальная к поверхностям тока. Другие необходимые компоненты берутся в зависимости от рассматриваемого сечения. Например, во входном сечении / рабочего колеса радиально-осевой турбины = nDip bp, где bp - высота входного отверстия колеса, н по (3-7) -5- . (3-8) nDipbp Окружная составляющая v зависит от условий выхода потока из направляющего аппарата и по (3-4) будет равна: Vou (3-9) 3 Заказ № 2265 Зная Vi и по (3-6) Абсолютная скорость на входе в рабочее колесо представляется векторной суммой (рис. 3-4, б) Vi = Vi-fVi . (3-10) 60 строим параллелограмм скоростей и определяем w (рис. 3-4, е). Форма входного параллелограмма скоростей зависит от угла между % и и Pi между щ-ц j. Часто вместо параллелограмма строят треугольник скоростей (изображен пунктиром). В выходном сечении рабочего колеса 2:  Рис. 3-5. Траектории абсолютного движения жидкости в радиально-осевой турбине. 60 F, Кроме того, поскольку решетка лопастей рабочего колеса весьма густая, то можно приближенно считать, что относительная скорость направлена по касательной к лопасти, т. е. P, = S,. (3-11) Из этого условия согласно (рис. 3-4, б) sin So (3-12) Имея Uj и Wa, согласно (3-5) строится параллелограмм, как показано на рис. 3-4, в, и находится Vj. Форма выходного параллелограмма определяется углами и р^. Треугольник скоростей изображен пунктиром. Можно построить треугольники скоростей не только для входного и выходного сечений, но и для промежуточных. Эти треугольники определят соответственные векторы v,-, и по ним можно провести траектории абсолютного движения жидкости в рабочем колесе. Вид таких траекторий показан на рис. 3-5. Следует обратить внимание на весьма важный вывод, что форма траекторий абсолютного движения не зависит от значения скорости V, а определяется только ее направлением. Если крышка и обод рабочего колеса турбины были бы прозрачными, то форму траекторий абсолютного движения можно было бы получить на фотографии, снятой неподвижным фотоаппаратом. У осевых турбин поверхности тока в рабочем колесе близки к цилиндрическим (рис. 3-6, а), т. е. Djp = Dp == Dp, расчетный диаметр можно вычислить как средний по площади D = Ko.5(D? + /.J. (3-13) 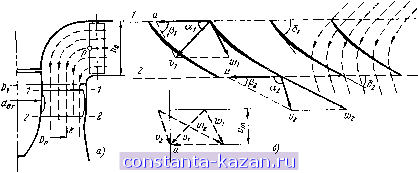 Рис. 3-6. Поток в осевой турбине. Развертка цилиндрического сечения рабочего колеса показана на рис. 3-6, б. Особенность состоит в том, что я£)рП 4Q n[D\-d Скорость на входных кромках 1 определяется как векторная сумма Vl = Vi -f Vi , причем Vi находится по (3-9). Абсолютная скорость Vj строится по (3-5) с учетом (3-11) и (3-12). Полученные в результате параллелограммы скоростей показаны на рис. 3-6, б. Треугольники скоростей на входной и выходной кромках совмещены (показаны пунктиром), поскольку они имеют одинаковые основание и и высоту v. Здесь же справа пунктирными линиями показаны траектории абсолютного движения жидкости в рабочем колесе. 3-3. РЕЖИМ РАБОТЫ ТУРБИНЫ приведенный в § 3-2 способ построения параллелограммов (треугольников) скоростей показывает, что для данного рабочего колеса при неизменном открытии направляющего аппарата ( о = = const) форма параллелограммов скоростей, определяемая углами аир, зависит от частоты вращения п и расхода Q. Рассмотрим , как эти параметры влияют на течение. Пусть расход Q сохраняется, а изменяется частота вращения п. При этом на входных кромках 1 лопастей рабочего колеса будет сохранять неизменное значение, так как согласно (3-10) не зависит от п. Изменяться будут только % и w, как показано на рис. 3-7, а. Из построения видно, что вектор относительной скорости меняет свое направление. При малой частоте вращения он отклоняется в сторону вращения > бр а при большой - в противополол<ную 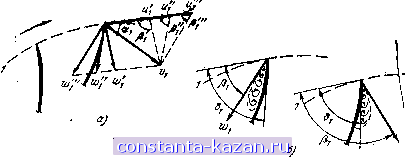 Рис. 3-7. Течение на входных кромках лопастей рабочего колеса. 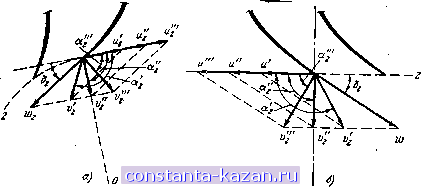 Рнс. 3-8. Течение на выходных кромках лопастей рабочего колеса. сторону р™ < б,. Когда Pj б натекание жидкости на входную кромку лопасти происходит под углом, что, как показано на рис. 3-7, б, сопровождается образованием вихревых зон, создающих дополнительные потери энергии (потери на удар). Наиболее благоприятным является режим безударного входа, когда Pi = б^. На выходных кромках 2 относительная скорость согласно (3-12) зависит только от расхода Q и угла 62, т. е. не зависит от п. Однако поскольку и^ пропорционально п, то по (3-5) абсолютная скорость V2 будет зависеть и от п. Эту зависимость легко проследить по параллелограммам скоростей на выходных кромках рабочего колеса радиальио-осевой (рис. 3-8, а) и осевой турбины (рис. 3-8, б). Они показывают, что с ростом п я и^ угол уменьшается и вектор Va поворачивается в сторону вращения. При этом можно отметить следующее: 1. Хотя расход постоянен, значение скорости зависит от п и минимальное ее значение соответствует условию, при котором вектор t 2 лежит в меридианной плоскости (направлен к центру или параллелен оси вращения), т. е. когда = 90°. 2. В общем случае поток за рабочим колесом имеет закручен-ность (циркуляция Г2 =7 0), причем если < 90°, то направление крутки потока совпадает с направлением вращения рабочего колеса, если же щ > 90°, то поток вращается в обратном направлении. Только при аа = 90° циркуляция Г2 = 0. Режим, соответствующий условию = 90°, когда минимально, а Га = О, называют режим нормального выход а. Поскольку потери на выходе из рабочего колеса в общем пропорциональны t 2, то режим работы турбины, близкий к режиму нормального выхода, дает наименьшие потери, т. е. является наиболее благоприятным. Режим, при котором одновременно удовлетворяются и условия безударного входа и нормального выхода, дает минимальные потери, т. е. наивысший к. п. д. турбины. Такой режим называют оптимальным. 3-4. ОСНОВНОЕ ЭНЕРГЕТИЧЕСКОЕ УРАВНЕНИЕ ТУРБИНЫ Для определения силовых и энергетических показателей потока в рабочем колесе применим закон момента количества движения в форме (3-3), который уже использовался. В качестве общего случая рассмотрим рабочее колесо радиально-осевой турбины,меридианное сечение которого показано на рис. 3-9. Выделим ограничивающими (контрольными) поверхностями, проходящими перед входными кромками / и за выходными кромками 2, а также поверхностями верхнего и нижнего обода объем, заключающий в себе все лопасти рабочего колеса. Для установившегося осред-, ненного потока внутри выделенного объема у„г не изменяется во времени и, следовательно, d(y r) равно разности Wiu !-г^г-Протекающая через рабочее ко- Рис 3-9. Скорости на входной и вы-лесо за время dt масса жидкости ЗД кромках лопастей рабочего КОЛсСа. т ~ pQ dt. s - меридианное сечение. 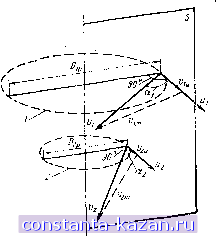 |
|
© 2025 Constanta-Kazan.ru
Тел: 8(843)265-47-53, 8(843)265-47-52, Факс: 8(843)211-02-95 |