В ЭТИХ условиях закон момента количества движения вместо (3-3) представляется формулой

d (mVuT)

(3-14)

Сумма моментов относительно оси вращения внешних вил 2 о действующих на выделенный объем жидкости, определяется следующим образом. Момент от сил давления на поверхности вращения 1 и 2 и поверхности ободов равен нулю. Силы веса также не дают момента, так как центр их приложения совпадает с ясью. Остаются силы трения по ограничивающим поверхностям и силы давления и трения жидкости на лопастях. Обе группы сил дают момент относительно оси, но первую из-за малости можно не учитывать, и остается момент, воздействующий на жидкость со стороны лопастей рабочего колеса М. Искомый же момент, создаваемый жидкостью на лопастях, будет равен - М.

В итоге по (3-14), раскрывая значения Ui и и2 > а также заменяя г на D/2, получаем:

УН = pQ(0,5Z)ipUiCOsai-O.SDapUaCosaa). (3-15)

Используя выражения средней циркуляции, аналогичные (3-2)

Ti = nDipDj cos ai и Гг = nDpV cos a.

(3-16)

можно выразить момент рабочего колеса через разность средних циркуляции на входе и выходе

М = (Г,-Г,).

(3-17)

Последняя формула особенно наглядна. Она показывает, что на рабочем колесе возникает крутящий момент только в том случае, когда оно воздействием своих лопастей меняет циркуляцию попюка. Следует отметить, что согласно (3-4) циркуляция на входе равна циркуляции, создаваемой направляющим аппаратом, т. е. = Го.

Знак Г принимается положительным, если v cos а совпадает с направлением окружной скорости и.

Зная момент и задавая угловую скорость рабочего колеса, можно определить развиваемую им мощность

Np. = Ma. (3-18)

Здесь М - в Н-м, (й - в 1/с, Яр. - в Вт. В то же время известно, что мощность турбины выражается формулой (1-19). Это позволяет составить равенство

где Н - напор турбины; т) - гидравлический к. п. д.

Подставляя в эту формулу М по (3-15) и учитьшая, что ©0,5Z)ip = = 1 и (О 0,5D2p = 2 - окружные скорости, получаем:

Ят1г = - ( it i cos ai-U2V2 cos а). 8

(3-19)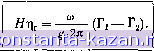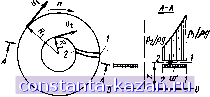

Рис. 3-10. К уравнению Бернулли для относительного движения.

Используя формулу (3-17), приходим к другой форме выражения

(3-20)

Формулы (3-19) и (3-20) представляют собой основное уравнение турбин, или уравнение Эйлера. Левая часть Ят]г - энергия в Дж, полученная рабочим колесом от жидкости весом в 1Н, прошедшей через лопастную систему рабочего колеса. Правая часть содержит кинематические параметры потока при входе на рабочее колесо и после выхода из него.

Таким образом основное уравнение дает связь между энергетическими и кинематическими параметрами в турбине.

Из уравнения Эйлера в форме (3-20) можно сделать важные выводы.

1. Выше отмечалось, что наиболее благоприятный по к. п. д. режим работы близок к условиям нормального выхода, когда циркуляция Гг = О или мала. Fi = Го - циркуляции, создаваемые направляющим аппаратом. Отсюда можно определить требуемое значение Го в зависимости от Я и ©.

2. В процессе прохождения воды через рабочее колесо турбины циркуляция потока должна убывать. Следовательно, рабочее колесо срабатывает циркуляцию, созданную направляющим аппаратом.

Представляет интерес другой вывод уравнения Эйлера, позволяющий несколько глубже понять механизм преобразования энергии рабочим колесом турбины, а именно вывод, основанный на уравнении Бернулли. Однако в данном случае нужно использовать уравнение Бернулли, записанное для относительного движения. Представим себе, что имеется диск, вращающийся с частотой п, об/мин (рис. 3-10), на котором укреплена трубка 1-2. По трубке от сечении 1 к сечению 2 движется жидкость со скоростью w (относительно трубки). В данном случае уравнение Бернулли для плоскости сравнения О-О имеет вид:

Ч 2g

2g 2g

(3-21)

Здесь Л|.2 - потери напора на участке 1-2; Ui и Mj - окружные скорости (переносные).

Особенность состоит в том, что в рассматриваемых условиях удельная энергия жидкости при движении вдоль трубки может убывать или возрастать в зависимости от изменения переносной скорости ui и uj. Это свойство и используется в рабочем колесе турбины, каналы которого, образованные лопастями, представляют собой систему трубок .

Из уравнения (3-21) следует, что

- г, =

w\ - w\

ре pg 2g 2g

Удельная энергия жидкости при входе на рабочее колесо

1-2-

(3-21)

1 =

pg 2g

Удельная энергия жидкости при сходе с рабочего колеса

+ 2 +

2

Разность удельных энергий

= р. к-

pg pg I 2g 2g

Заменив выражение в скобках правой частью (3-2Г), получим:

W7,--W,

u-. - ul,

+ h,n +

Записав Яр - /г,.2 = Яп , приходим к еще одной форме уравнения Эйлера

2 2

Яг1г =----\.

2 2

vi - vi

w\ - w\

(3-22)

которая особенно ясно показывает прямую зависимость НЦт от треугольников скоростей иа входе и выходе рабочего колеса. Уравнение (3-22) объясняет связь формы рабочего колеса с напором турбины. В осевых турбинах 1 = 2 и, следовательно, Ят1г определяется только абсолютными и относительными скоростями, которые ие могут быть слишком большими, так как иначе возрастут потери. Это и вызывает ограничение использования осевых турбин по напору. С ростом Н Переходят на диагональные и радиально-осевые турбины, у которых действует и различие переносных скоростей % и 2, причем, чем больше Я, тем роль этого фактора возрастает. Этим объясняется то, что у высоконапорных турбии увеличивается отношение DjDi (см. рис. 2-29, 2-26 и 2-30).

3-5. ОСОБЕННОСТЬ РАБОЧЕГО ПРОЦЕССА КОВШОВЫХ ТУРБИН

Отличие активных ковшовых турбин (§ 2-7, рис. 2-31) от реак тивных состоит в том, что у них: 1) рабочее колесо вращается в воз духе и может использовать только кинетическую энергию жидко сти и 2) вода одновременно воздействует только на часть лопастей-

Эти два фактора определяют и некоторые особенности рабочего процесса ковшовых турбин.

При всех открытиях направление и величина скорости струи Ое (2-5) сохраняются постоянными (коэффициент ф изменяется очень мало). Скорость на входной кромке лопасти 1 (рис. 3-11) практически равна скорости струи

= Ус-Окружная скорость (переносная) для данного сечения лопастей, расположенного на расстоянии г от оси вращения, определяется выражением

l = = г =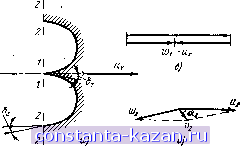

Рис. 3-11. Кинематика потока в рабочем колесе ковшовой турбины.

(среднее значение /р -= 0,5 Di на рис. 2-31).

При этом параллелограмм скоростей Wi = Vi - - Ui на входной кромке лопасти вырождается впрямую линию (рис. 3-11,6) и w-i совпадает с направлением струи. Следовательно, для приближения к условиям безударного входа угол входной кромки 61 (рис. 3-11, а) должен быть минимальным ( нож ).

Параллелограмм скоростей на выходной кромке определяется тем, что в процессе движения по лопасти относительная скорость изменяется мало, и можно принять = w, а ее направление совпадает с 62. В иноге получаем (рис. 3-11, е):

V2 = W2-1-U;..

Поскольку угол 62 мал, параллелограмм получается вытянутым и, несмотря на значительные составляющие скоростей и Ur, скорость 02 оказывается небольшой. По аналогии с рис. 3-8 легко убедиться, что изменение пни, при сохранении Q и ш приведет к изменению угла и скорости v. Минимальное значение соответствует = 90° - условию нормального выхода.

Кинематика течения жидкости показывает, что рабочее колесо ковшоюй турбины также меняет момент скорости жидкости относительно оси вращения и, следовательно, для определения момента рабочего колеса можно использовать зависимость (3-14). В итоге можно получить и уравнение Эйлера в форме (3-19) и (3-22) [форма (3-20) не подходит, так как здесь нельзя использовать определение циркуляции].

Выражение (3-22) позволяет прийти к интересным результатам. Если иметь в виду, что окружные скорости на входных и выходных кромках равны (ui = 2), а относительная скорость по мере движения по лопасти за счет трения несколько убывает (w < w, то из (3-22) следует:

Учитывая, что согласно (2-5) и принятому условию v= x?j2g- (р^Я, получаем:

..:г ..:г

Лг = ф*-

- wl vl

(3-23

2gH 2gH

Формула (3-23) показывает, что гидравлический к. п. д. rir слагается из трех частей, учитывающих потери в сопле, потери на лопастях и выходные потери, равные у|/2§Я. Это является обоснованием необходимости обеспечения особо гладкой рабочей поверхности лопастей и уменьшения с целью улучшения энергетических качеств ковшовой турбины.

3-6. ТУРБИНЫ ОДНОГО ТИПА

И ЗАКОНЫ ПОДОБИЯ РЕЖИМОВ ИХ РАБОТЫ

Тип турбины определяется формой ( геометрией ) ее проточного тракта. Иными словами, все турбины данного типа имеют геометрически подобную проточную часть. Следует подчеркнуть, что размер турбины не участвует в определении ее типа.

В соответствии с принятым определением две турбины одного типа, но различного размера удовлетворяют следующим условиям:

1) все соответственные углы в них равны:

би = 612, = 622, бд = 6,2; 2) отношение всех соответствующих размеров постоянно:

Da 602

(3-24)

(3-25)

Режимы турбин одного типа будут подобны, если сохраняется геометрическое подобие параллелограммов или треугольников скоростей в соответствующих точках проточного mpoKtna. Следовательно, при подобии режимов:

1) направления всех соответствующих скоростей должны быть одинаковыми, т. е. все соответственные углы равны:

и = 12. 21= 22, Pii = Pi2- (3-26)

В связи с этим свойством иногда подобные режимы называют изогональными;

2) отношения всех соответствующих скоростей должны быть постоянными:

11-

(3-27)

Установим теперь на основании приведенных определений закономерности, определяющие соотношения между параметрами турбин одного типа в условиях подобия режимов их работы.

Задача. Имеем две турбины одного типа, но различного размера Di и Dj. Углы открытия направляющего аппарата и лопастей рабочего колеса равны: = ао2 и = фа.

Каковы должны быть соотношения частот вращения и п^, расходов Qi и Q2 и мощностей и N, чтобы режимы работы обеих турбин были подобны?

Решение. Прежде всего используем геометрические (3-24), (3-25) и кинематические (3-26), (3-27) соотношения.

На основании (3-6)

По (3-8) имеем:

(3-28)

Учитьшая, согласно (3-25) V/oa = Di/D, получаем:

(3-29)

fim2 QiD]

Поскольку no (3-27) при сохранении режимов Un/ i2 = хтх/хшг.

приходим к равенству

Dili О2П1

или

Обобщая этот результат, записываем кинематическое условие подобия (сохранения) режима работы турбины

= const.

(3-30)

Теперь используем энергетические соотношения, учитывая, что эти турбины работают при разных напорах Hi и и имеют гидравлические к. п. д. riri и ц^-

Напишем уравнение Эйлера в форме (3-19) для каждой из турбин

gfiin = 1Л1 cos и-U2it 2i cos 21; (3-31)

gH гЛга = 1212 cos - 2222 cos 22- (3-31)

Из условий подобия (3-26) и (3-27) и из формулы (3-28) следует.

что

11 = 12; 21 = 22 И ii/ i2 = yii/iia = 2i/ 22=f 21/*22 = ini/Z):