Характерными видами (рис. 5-5) кавитации в гидравлических машинах являются: а - профильная, возникающая при обтекании лопастей в области наиболее низкого давления; б - щелевая при протекании жидкости с большим перепадом давления через зазоры, например между лопастями рабочего колеса и камерой, и б - местная, вызываемая обтеканием неровностей, отдельных уступов, ребер и др., например головок болтов.

Область возникновения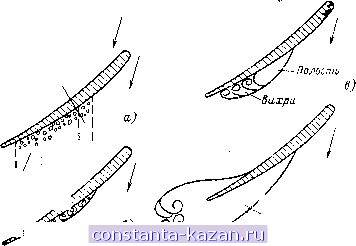

Область зосхлопыбаная

Полость

Вихра

Рис. 5-6. Стадии лопастной кавитации.

Кавитация, в основном профильная, может иметь различные формы или стадии развития, показанные на рис. 5-6. Здесь а - пузырьковая форма кавитации, при которой разрывы сплошности имеют вид отдельных движущихся пузырьков - каверн; б - зональная или пленочная, характеризующаяся наличием сплошной каверны, заполненной пульсирующими вихрями жидкости; в - отрывная, когда в каверне имеется полость, не заполненная жидкостью, иг - суперкавитация, при которой полость настолько развита, что она замыкается за пределами профиля.

Каждая из этих форм имеет свои специфические особенности. Пузырьковая и зональная формы наиболее интенсивно проявляются в акустическом (шум) и эрозионном воздействии, но сравнительно мало сказываются на гидродинамических характеристиках потока, в то время как отрывная, а тем более суперкавитация существенно меняют гидродинамические показатели потока, что влияет на расход, мощность и к. п. д. гидромашин.

На основании приведенного рассмотрения условием отсутствия кавитации является

Ра1>Рв. ш

(5-2)

т. е. абсолютное давление в любой точке проточного тракта должно быть выше давления насыщенного пара жидкости.

5-2. КОЭФФИЦИЕНТ КАВИТАЦИИ

И ДОПУСТИМАЯ ВЫСОТА ОТСАСЫВАНИЯ

Условие отсутствия кавитации в форме (5-2) является общим, но чтобы его использовать, нужно знать распределение давления во всех точках проточного тракта турбины. Поскольку такими данными, как правило, не располагают, то используют косвен ные показатели.

Абсолютное давление в некоторой точке с (рис. 5-7) рабочего колеса можно представить соотношением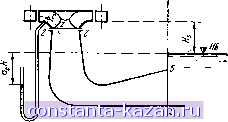

Рис. 5-7. К определению коэффициента кавитации.

АР2-.. (5-3)

в котором Ра2~ ЗбСОЛЮТНОС

давление в сечении 2-2, а р2 с - дополнительное понижение давления в точке с относительно сечения 2-2.

Величину Pn2/pg определяем по (4-10), имея в виду (1-8) и представляя потери в отсасывающей трубе по формуле

Тогда

Раа Ратм

pg pg

-Hs-

Sot

: (5-4)

2g 2g --2g

В (5-4) выражение в скобках представляет собой среднее динамическое понижение давления [Ah a по (4-15], создаваемое отсасывающей трубой. Можно показать, что Ah пропорционально напору. Действительно, используя (3-37), имеем:

.2 = .

(5-5)

где Q\ - приведенный расход; - коэффициент площади сечения. Отсюда

(5-6)

По смыслу входящих в выражение (5-6) коэффициентов ясно что они.а следовательно, и адс сохраняют неизменное значение при подобных режимах. В итоге pJpg представляется формулой

Раг Ратм pg pg

(5-7)

Дополнительное понижение давления в точке с рабочего колеса также пропорционально напору

(5-8)

Это можно доказать, написав уравнение Бернулли для относительного движения в форме (3-21) для струйки с-2 (рис. 5-7). При этом получим, что Др2.(, с точностью до разности Z пропорционально и ы^, а последние, как это следует из (5-5), пропорциональны напору.

Подставляя (5-7) и (5-8) в (5-3), находим выражение

Рас Ратм

pg ~ pg

(5-9)

+ а„. к - коэффициент кавитации, показывающий . относительное динамическое понижение пьезометрического уровня (давления) в точке с.

Для различных точек рабочего колеса значение а^. меняется. Наибольшее его значение для данного режима, соответствующее точке, где давление минимально, есть коэффициент кавитации турбины а^.

Из (5-9), зная и имея в виду (5-2), записываем условие отсутствия кавитации

pg pg pg

или

а,Н, (5-11)

(5-10)

Рв. п

т. е. для обеспечения отсутствия кавитации в турбине необходимо ограничивать высоту отсасывания Н^.

Атмосферное давление зависит от абсолютной отметки над уровнем моря, и приближенно эта зависимость представляется формулой

= 10,3 -

(5-12)

pg 900

где V - абсолютная отметка (считается для нижнего бьефа).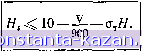

Для холодной воды можно принять Pe.Jpg = 0.3 м (рис. 5-1). в этих условиях (5-11) приобретает вид:

(5-13)

Формула (5-13) широко используется при определении допустимой высоты отсасывания и назначении отметки установки турбины при проектировании ГЭС.

Определение коэффициента кавитации производится экспериментальным путем на модельной установке (см. гл. 6).

Запишем выражение (5-10) в форме уравнения

Рн.б

Здесь вместо

Рв. п

стоит

(5-14)

Ри.б -

давление над нижним бьефом, а вместо От стоит Оу - коэффициент кавитации установки, который определяется формулой

Ри.б

Рв. п

н

(5-15)

Рис. 5-8. Измеиеиие к. п. д. в зависимости от коэффициента кавитации установки.

Модельная установка работает при постоянном напоре и режим сохраняется неизменным, изменяется только Оу, например уменьшается за счет снижения давления р„. g (над нижним бьефом создается разрежение). По полученным опытным значениям к. п. д. турбины строится У] = f (Оу), показанный на рис. 5-8. С уменьшением Оу ДО некоторых пор т] сохраняет свое значение, но затем начинает резко падать. Поскольку режим работы сохраняется и изменяется ТОЛЬКО коэффициент кавитации, это указывает на возникновение кавитационного срыва, на развитие в турбине кавитационных явлений (если модель прозрачна, то их можно обнаружить и визуально).

Величина Оу непосредственно при срыве представляет собой критический коэффициент кавитации (обозначается а).

При расчетах допустимой высоты отсасывания по (5-13) расчетный коэффициент кавитации турбины определяют по критическому значению а с введением коэффициента запаса к^,:

(5-16)

который принимается ka = 1,1 -ь 1,2.

Кавитация и допустимая высота отсасывания турбин

[Гл. 5

Пример 5-1. Определить допустимую высоту отсасывания Hg для турбины с напором Я= 60 м при отметке нижнего бьефа 360 м, если по характеристике а= 0,1.

Решение. Задаемся коэффициентом запаса ka- 1,15. Тогда по (5-16)

ат= 1,150,1 =0,115,

Рис, 5-9. Отсчет высоты отсасывания в различных турбинах.

По (5-13) вычисляем:

WslO - -- 0,115-60= 10-0,4- 900

-6,9 = 2,7м.

Турбину можно установить на 2,7 м выше отметки нижнего бьефа. Пример 5-2. Какова будет допустимая высота отсасывания, если для условий примера 5-1 применить другую турбину, у которой а= 0,2.

Решение. При том же коэффициенте запаса ka~ 1,15; по (5-16)

ат= 1,15-0,2 = 0,23!

по (5-13)

1,д

1,0 0,9

о,в

0,7 0,6 0,5

о, г

10-52-0,23.60 =

-4,2 м.

= 10 - 0,4-13,8 =

Турбину придется установить так, чтобы она была заглублена под уровень нижнего бьефа на 4,2 м.

Способы отсчета высоты отсасывания для различных турбин показаны на рис. 5-9. В вертикальных радиально-осевых и диагональных турбинах Hs отсчитьшается от нижней кромки направляющего аппарата (часто высоту отсасывания отсчитывают от средней линии направляющего аппарата, тогда Hs = Hs -f 0,5Ьо); в вертикальных осевых - от оси поворота лопастей рабочего колеса. В горизонтальных турбинах Н^ отсчиты-вается от верхней точки рабочего колеса.

о 100 гоо 300 00 50о еоо то воо 900

Рис. 5-10. Зависимость коэффициента кавитации турбины от быстроходности при полной нагрузке.

§ 6-1

Виды характеристик

Коэффициент кавитации турбин а зависит от режима работы и типа турбины, от ее коэффициента быстроходности rts. Для условий номинальной мощности турбины зависимость а = / (п^иом) показана на рис. 5-10, причем дан диапазон возможных отклонений для различных типов турбин. Среднее значение а для этих условий можно вычислить по эмпирической формуле

(ns иом -f 30) 200 000

(5-17)

Приведенные зависимости показывают, что с ростом быстроходности турбины коэффициент кавитации быстро увеличивается.

ГЛАВА ШЕСТАЯ

ХАРАКТЕРИСТИКИ ТУРБИН 6-1. ВИДЫ ХАРАКТЕРИСТИК

В процессе проектирования гидроэлектростанций, при выборе типов турбин и определении их основных параметров, размеров, частоты вращения, к. п. д., отметки установки и других факторов, а также при назначении наиболее целесообразных условий использования оборудования в процессе эксплуатации необходимо иметь достаточно полные данные о свойствах турбин. Эти данные представляются в форме характеристик, определяющих все нужные показатели турбины для различных условий ее работы, точнее, для различных режимов.

Из рассмотрения рабочего процесса в гл. 3 следует, что показатели работы турбин должны определяться двумя факторами:

1) геометрическими, которые фиксируются формой проточной части (тип турбины), размером (диаметр Di) и открытием направляющего аппарата или иглы а (Для поворотно-лопастных турбин, имеющих двойное регулирование, кроме того, еще и углом установки лопастей рабочего колеса ср);

2) кинематическими, фиксирующими режим работы турбины. Последние должны включать две независимые переменные rt и Q по (3-30). Если выразить условие подобия режимов по (3-32), то получим:

= const. (6-1)

У Япг

Следовательно, для данного D и к. п. д. переменными, определяющими режим, будут па Н. Для турбин это удобнее, чем (3-30). так как напор обычно задается, а расход определяется.