рис. 3-7), циркуляционные при выходе с рабочего колеса (см. рис. 3-8), выходные (см. рис. 4-17).

Механические потери вызываются трением, связанным с вращением вала и рабочего колеса турбины. Сюда относятся потери в подшипниках и уплотнениях N и так называемые дисковые потери, возникающие в результате трения вращающихся частей о жидкость, например в зазорах между ободами рабочего колеса и корпусом (крышкой). Мощность, теряемая на дисковое трение Л^диск. определяется формулой

Ы , = РпЮК (6-9)

Здесь Р - коэффициент, зависящий от п и D. Оказывает влияние и зазор (подробнее - см. [24, 25]).

Объемные потери вызываются внутренними перетоками воды в турбине из области высокого давления в область низкого давления в обход рабочего колеса. С целью снижения объемных потерь в радиально-осевых турбинах применяют щелевые и лабиринтные уплотнения (см. рис. 2-26, 2-29, 2-30), в осевых и диагональных турбинах уменьшают зазор между лопастями и камерой рабочего колеса (см. рис. 2-13).

Каждый из видов потерь мощности можно представить в форме потери напора. Например, если мощность, теряемая на гидравлические потери Nr, записать в форме = 9,81 Qh, то

/1, = -, (6-10)

9,81Q

где Q - полный расход, поступающий в турбину.

Аналогично можно найти механические потери h и др. Более показательны относительные потери, взятые по отношению к напору турбины Я. Например, 1 - т] = Н^/Н, откуда гидравлический к. п. д.

т = 1-. (6-11)

Гидравлические потери также можно разбить на отдельные составляющие: потери в подводящем тракте и рабочем колесе Лп. р, потери в отсасывающей трубе Лос. выходные потери h:

/1г = /1п.р+/1отс + Лвых- (6-12)

Аналогично механические потери Л^х определяются выражением

где iV ex - мощность, расходуемая на механические потери, и Q - расход турбины,

Объемные потери находятся из выражения /Vo6 = 9.81o6 = 9,81Q/io6.

где yVo6 - мощность, соответствующая объемным потерям; об - объемные потери (расход перетоков); Я ~ напор турбины. Отсюда получаем:

/1об=Я.

С учетом изложенного к. представится выражением

(6-14)

т, = 1.

н

(6-15)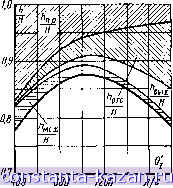

Рис. 6-12. Балансовая характеристика поворотно-лопастной турбины.

Наиболее полное представление о составе и изменении потерь в турбине для различных режимов дает балансовая характеристика.

В качестве примера на рис. 6-12 показана балансовая характеристика модели поворотно-лопастной турбины

(rtj = 130 об/мин на рис. 6-10), из которой видно, что механические потери относительно невелики, около 0,02, и от режима зависят мало. Основными являются гидравлические потери (сюда входят и объемные, поскольку выделить их не представляется возможным), но соотношения различных их видов существенно зависят от режима.

Пересчет гидравлического к. п. д. с модели на условия натуры

Представим все гидравлические потери в турбине в форме

Лг = Сх-, (6-16)

причем скорость и, к которой относится коэффициент потерь Сг. может находиться по любому сечению тракта.

Поток в турбине чрезвычайно сложен, и пока еще нет сколько-нибудь полного представления о закономерностях формирования в нем гидравлических потерь. Приходится вводить упрощения. Можно принять, что коэффициент потерь состоит из двух частей

~ Смести Ь тр I

где Смести - коэффициент потерь, аналогичный коэффициенту местного сопротивления, а - коэффициент потерь на трение по длине обтекаемых поверхностей.

Для оценки изменения Сгр в качестве аналога используем зависимость сопротивления при обтекании тонкой пластинки (рис. 6-13). Сила сопротивления, вызываемая трением Р^, определяется формулой

P, = CfFp

(6-17)

в которой F - площадь пластинки; v - скорость натекания; о - плотность жидкости. Коэффициент сопротивления зависит

от относительной шероховатости IIА (Д - эквивалентный выступ шероховатости), и от числа Рей-нольдса

Z IS

(6-18)

Рис. 6-13. Коэффициент сопротивления трения пластинки.

где V - скорость; v - кинематическая вязкость (для воды V = = 0,01 м^/с^). Эта зависимость для прямоугольной пластинки шириной В и длиной / показана на рис. 6-13.

Приведенные данные показывают, что для гладкой поверхности с ростом Re коэффициент Cj убывает. Согласно формуле Кармана для пластинки при турбулентном пограничном слое

Фактические значенияКе для турбин позволяют приближенно принять, что сопротивление, вызываемое трением, изменяется, как для гладкой поверхности, по (6-19).

Совершенно очевидно, что Cip пропорционален Cf и, следовательно, можно записать:

тр. м

Здесь /irp. м и Кр ~ потери трения в модели ивнатур ной турбине; Ум и и - соответственные скорости.

Используя соотношение (5-5) для подобных режимов

получаем:

или с учетом (6-19)

Cf Н

тр тр. м . ftxp fcrp.m /КемN 2

Н Ям I Re j

(6-20)

Положим, что потери трения в модели составляют некоторую часть от общих гидравлических потерь

/тр. м - г. м>

тогда, если гидравлический к. п. д. модели ц , то относительные потери составляют:

а) местные (вихревые)

= (1-е)

Йместп. м п -= (1 -е) (I -Ц,. );

Я

б) на трение

Я h-T. и

Йтр^ Я Я

= е(1-Лг.м)-

Выразим теперь гидравлические потери в натурной турбине. Они также будут слагаться из потерь местных и на трение:

1-Т1г =

Умести I p

н н

Местные относительные потери для натуры такие же как и

в модели, потери же на трение представляются формулой (b-2U). В итоге получаем: 2 1-т1,= (1-е) (1 -11г. м) +е (1 -т), м) .

Учитывая (6-18) и формулы подобия, можем представить отношение

Нем

DmV Л Ям

При равенстве кинематических коэффициентов модели и натуры v = V формула пересчета гидравлического к. п. д. (точнее, потерь) с модели на натуру приобретает вид:

1-Т]р=(1-TIp.m)

(6-21)

ИЛИ поправка на гидравлический к. п. д. от модели в натуре согласно (6-21) составляет:

ДЛг = Пг--Пг.м;

ATlr=(l-Tlp. )e(l-7 (6-22)

Следует иметь в виду, что формулы (6-21) и (6-22) получены при целом ряде допущений, поэтому при использовании их необходимо учитывать данные опыта:

1) для поворотно-лопастных турбин в зоне рабочих режимов принимают 8 = 0,75; для радиально-осевых турбин

при^;<<3;опт 8 = 0,25+0,5-4;

1опт

при Q;>Q; , 8 = 0,75;

2) для предварительных расчетов Ari можно определять только для оптимального режима при 8 = 0,75, сохраняя значение А-Пг для всех режимов

Пг = Лг.м+Аг1р; (6-23)

3) к. п. д. ковшовых турбин для натуры не пересчитывается и принимается таким же, как и на модели.

6-5. ПОСТРОЕНИЕ ЛИНЕЙНЫХ ХАРАКТЕРИСТИК

по ГЛАВНОЙ УНИВЕРСАЛЬНОЙ ХАРАКТЕРИСТИКЕ

Обычно требуется построить характеристику для конкретной турбины данного типа. Поэтому у всех характеристик определяющим параметром является диаметр турбины Dj. Необходимые для линейных характеристик еще два параметра зависят от вида линейной характеристики.

Для построения любой характеристики предварительно нужно:

1) установить поправку на к. п. д. Air по (6-22). Следует учитывать, что в нормальных режимах механические и объемные потери составляют 1,5-2%;

2) установить запас на коэффициент кавитации fe по (5-16). Это позволит найти допустимое значение высоты отсасывания.

Ниже рассмотрены способы построения некоторых наиболее часто используемых линейных характеристик (рис. 6-14).

Линейная расходная и мощностная характеристики (рис. 6-14, а и б) представляют собой сечение главной универсальной характеристики прямой а-а, отвечающей условию rtj = const (рис. 6-15):

nD ,

На этой линии наносится несколько точек и для каждой вычисляются необходимые параметры: Q, ц, N, сг, Hg, о и др.

На этих характеристиках существенное значение имеют линии /V a e. 0,95 Ломаке и х. X - открытие холостого хода.

095Н,

а) б) iiKc в)

Рис. 6-14. Линейные характеристики турбин.

Линейная напорная характеристика (рис. 6-14, в) представляет собой сечение главной универсальной характеристики линией = const (линия b-b на рис. 6-15). На этой линии наносится несколько точек и для каждой вычисляются требуемые параметры. Напор, соответствующий каждой режимной точке, находится согласно формулам подобия

Е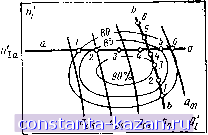

(6-24)

Здесь Пг/Пг. м - отношение оптимальных гидравлических к. п. д. натуры и модели.

На этой характеристике интересна точка -напор ХОЛО- Рис. 6-15. К построению линейных птпгп YOTTn характеристик по главной универ-

СТОГО хода. сальной.

Линейная оборотная характеристика

(рис. 6-14, г) также представляет собой сечение главной универсальной характеристики линией = const (линия b-b на рис. 6-15). Но здесь каждая точка определяет не напор, а частоту вращения

n=n\J, где/ = 11(6-25)

1 Dl 11г. м

разгонная частота враще-

Представляет интерес точка Празг ния.