Для нахождения силового взаимодействия между лопастями рабочего колеса и протекающей жидкостью используем уравнение момента количества движения в форме (3-14) для объема жидкости, ограниченного ободами рабочего колеса и контрольными поверхностями 1 и 2, проведенными по входным и выходным кромкам лопастей (рис. 10-6). В уравнении (3-14) Q - подача насоса, р - плотность перекачиваемой жидкости, причем

ViJi = 0,511 cos 1 и У2 Г2 = ОгУ2 cos аз-Моменты внешних сил относительно оси 0-0, действующих на выделенный объем жидкости, слагаются из момента, передаваемого лопастями насоса М, и момента сил трения, который не учитываем. Силы давления, нормальные к ограничивающим поверхностям, не дают момента относительно оси 0-0, так как либо направлены к центру (поверхности J и 2), либо лежат в меридианной плоскости (поверхности ободов). Таким образом, сумма моментов внешних сил, действующих на выделенный объем жидкости, сводится к крутящему моменту М, передаваемому жидкости лопастями рабочего колеса:

М = pQ{0,5D2 cos 2-0,5011 cos aj). (10-9)

Используя понятие циркуляции жидкости в форме (10-5), имеем на входе в рабочее колесо Гх = nDiVi cos и на выходе Г2 = = nDzVz cos 2. тогда выражение (10-9) можно представить так: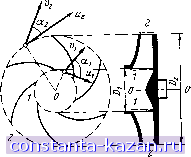

Рис. 10-6. К выводу основного уравнения лопастного насоса.

2п

(Г2-ГО.

(10-9)

Полученный результат показывает, что момент, развиваемый рабочим колесом, пропорционален массовому расходу и изменению циркуляции жидкости или ее момента скорости.

Зная момент, развиваемый рабочим колесом М, Н-м, и угловую скорость (О, 1/с (со = 2яп/60), получаем секундную энергию, т. е. мощность, которую развивает рабочее колесо, воздействуя на жидкость, определяемую произведением = Н-м/с = Дж/с =

= Вт. Если принять, что энергия, передаваемая рабочим колесом 1Н протекающей через него жидкости, равна Я^, то мощность, получаемая жидкостью, по аналогии с (9-8) составит pgQH., Вт. Приравнивая обе мощности и используя (10-9), получаем:

М(о = (opQ (0,5022 cos 2-0,5DiyiCOsai) = pgQH.,

откуда, учитывая, что 0,5Dcu = и - окружная составляющая скорости, приходим к выражению для теоретического напора насоса Н,:

или по (10-9)

(10-10)

(10-10)

Полученные формулы, представляющие собой основное уравнение насосов, или уравнение Эйлера, применимы к лопастным насосам любого вида. Они имеют очень большое практическое значение, так как дают связь между теоретическим напором и кинематикой жидкости, протекающей через рабочее колесо.

Выше отмечалось, что обычно близко к 90°, т. е. Fi = 0. Из уравнения Эйлера следует, что теоретический напор насоса определяется в основном произведениями сйГ2 или 2*2 cos 2. Чем эти произведения больше, тем больше и теоретический напор.

Действительный напор Я, развиваемый насосом, будет меньше теоретического за счет гидравлических потерь в самом рабочем колесе, а также в элементах подвода и отвода. Если гидравлические потери составляют h, то Я = Я^ - h. Вводя понятие гидравлического к. п. д.

Пг = -тг- ИЛИ Т1,. г--

получаем

H + hf

(10-11) (10-12)

Формула (10-12) совместно с уравнением Эйлера (10-10) или (10-10) позволяет найти выражения для действительного напора насоса

или

я 1 ,

-=-( 22 COS 2- А COS аЛ

Пг g

(10-13) (10-13)

Гидравлический к. п. д. насосов составляет ti = 0,7 0,93 (меньшие значения для малых насосов).

10-3. РЕЖИМ РАБОТЫ НАСОСА И УСЛОВИЯ ПОДОБИЯ РЕЖИМОВ

Условия работы насоса могут быть заданы двумя параметрами' подачей (расходом) Q и частотой вращения п. Как изменяются параллелограммы скоростей, если при постоянном значении п менять подачу Q, показано на рис. 10-7; а - для центробежного насоса и б - для осевого, для входной / и выходной 2 кромок лопастей рабочего колеса. При постоянстве п вектор и сохраняет свое зна-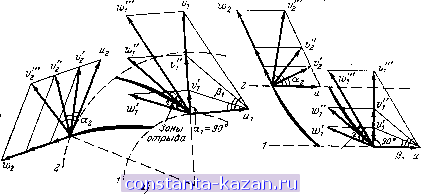

Зоны отрыва

Рис. 10-7. Изменение режимов работы насосов в зависимости от подачи при постоянной частоте вращения.

чение. Подачу характеризуют векторы v, которые, как видно из (10-2) (10-8), пропорциональны Q, индекс -соответствует малому Q, а индекс - большому.

На входе в рабочее колесо изменение Q вызывает изменение вектора и его направления Pi. С увеличением Q угол Pi увеличивается. Когда угол Pi мал (условия ) и когда он велик (условия ), вода входит под некоторым углом к входной кромке лопасти, что вызывает местный отрыв потока (создание вихревой зоны) и приводит к увеличению гидравлических потерь. При малых расходах зона отрыва расположена с тыльной стороны лопастей, при большом - с рабочей. Потери на вход будут минимальны, если Pi 6i, т. е. если угол Pi близок к углу входной кромки лопасти (рис. 10-1), что примерно соответствует у .

Условия, при которых Pi = 6i потери на вход в рабочее колесо минимальны, называют условиями безударного входа.

На выходе из рабочего колеса с уменьшением ислида уменьшается и угол вектора v. Это приводит, как видно

параллелограммов скоростей, к возрастанию окружной компо-

центы скорости cos и выходной циркуляции (рис. 10-5), что должно влиять и на потери и на напор насоса.

Выполненный анализ показывает, что условия работы лопастного насоса, т. е. его режим, определяются в основном углами параллелограммов скоростей, т. е. значениями а и fi. При сохранении углов а и Р режимы считаются кинематически подобными.

В связи с этим подобные режимы иногда называют изогональными.

Приведенное определение , позволяет дать математическое выражение условий подобия режимбв работы насоса, которое сводится к двум соотношениям:

1) отношение^всех соответственных скоростей должно сохраняться

£it = Bl = HiI= М- (10-14)

fi2 12 112 f22

2) соответственные углы параллелограммов скоростей должны быть равны

aii = ai2; а^сс; Ри = р22---- (10-15)

Отсюда выводятся кинематические условия подобия режимов работы насосов. Как отмечалось, условия работы насоса могут быть заданы в виде значений подачи Q и частоты вращения п. Используя формулы (10-2), (10-3) получаем: .

Uji nDiUi 60 12 60 nDiUi

Учитывая же соотношение (10-14), приходим к следующему условию:

J!lL = M.- Qf 1

tl2 12 Qi 2

которое и дает окончательное условие кинематического подобия режимов дляданногонасоса

- = const.

(10-16)

Тип лопастного насоса определяется формой (геометрией) его проточной части, а в основном - рабочего колеса. Насосы с геометрически подобной проточной частью представляют собой насосы одного типа, характеризующиеся следующими соотношениями (рис. 10-1):

1) отношение соответствующих размеров должно быть посто-

Da /?22

2) все соответственные углы должны быть равны

бп = б

621 = 6,

(10-18)

Пусть имеются два насоса с геометрически подобной проточной частью, т. е. одного типа, но с различными значениями и (здесь принимаются соответствующие диаметры, например, выходные рабочего колеса) с подачами и Q2 и частотами вращения и п^. Для них, используя те же формулы (10-2) и (10-3), получаем:

Qi nDjfca Qi /

fii

иц nDi i 60

12 60 nDjWa Согласно (10-9) при подобии режимов оба отношения должны

быть равны:

q2 \Di

Dill Dn

или

В результате приходим к общей формуле кинематического подобия режимов

(10-19)

= const.

Если в насосе может изменяться геометрия проточной части, например у осевых насосов угол установки лопастей рабочего колеса, то соотношение (10-19) применимо только для одних и тех же углов для различных насосов.

В кинематические условия подобия режимов (10-14) не был включен важный параметр - напор. Чтобы его учесть, необходимо рассмотреть энергетические зависимости.

Для некоторого режима работы насоса, определяемого параметрами Ml, Qi и Di, уравнение Эйлера можно записать в форме (10-13)

1 = у- ( 2121 cos 21 - 1Л t COS и) TJrt. (10-20)

Пусть параметры изменились на и (тип насоса тот же),

но подобие режимов сохраняется. Для новых значений параметров уравнение Эйлера имеет вид:

Яд = -- ( 2222 cos 22 - 2121 cos 21) 11г2-

(10-21)

Поскольку режимы подобны, то должны удовлетворяться условия (10-14) и (10-15):

22 = 21 И ai2 = ii;

22 22 12 v12 nD

21 21 11 Уц njOi

(10-22)

Используя соотношение (10-22), уравнение (10-21) можно преобразовать так

iOi

( 2121 cos 21-МцУц cos ц) ц,. (10-23)

Беря отношение (10-20) к (10-23) и принимая, что при подобных режимах сохраняется и гидравлический к. п. д. -ц^ = т), получаем:

/niDi2

el Я,

я. Do

(10-24)

Найденная связь между напорами, частотами вра111ения и диаметрами рабочих колес (10-24) с учетом общего кинематического условия подобия (10-19) позволяет записать общие формулы подобия режимов работы насосов:

Я1 /щ

(10-25)

(10-26)

Кроме того, используя формулу (9-10) и принимая t)i = получаем:

(10-27)

- Формулы подобия (10-25) и (10-26) имеют очень большое значение, так как позволяют пересчитывать параметры, определяющие работу насосов, их характеристики при изменении частоты вращения п, а также пересчитывать на условия натуры характеристики насосов, полученные на модельных установках, что особенно важно для крупных насосов.

10-4. КОЭФФИЦИЕНТ БЫСТРОХОДНОСТИ НАСОСОВ

Выше было показано, что насосы данного типа (геометрически подобные) могут выполняться различного размера и работать в широком диапазоне частот вращения, подач, напоров и мощности. Следовательно, для того чтобы характеризовать тип насоса, нужны какие-то показатели, приведенные к единым, стандартным условиям. Одним из таких показателей, широко используемых для лопастных насосов, является коэффициент быстроходности.

Коэффициент быстроходности данного насоса (п^) - это частота вращения геометр и-