Умножая формулу (1.24) на > е, получаем максимально допустимую мощность, которую можно передать гюнесимметричному полосковому волноводу, заполненному диэлектриком:

. а с = 37,98- 10(Д/й)ГвЛГ =Р, аксГГ

Умножением на У е формулы (1.88) находим максимально допустимую мощность, которую можно передать по симметричному полосковому волноводу, заполненному диэлектриком:

. а с = 12,1 5 1 0d= (0,1 + Д/d) (4 + b/d) 1/7= Я, акс

Точно так же из выражения потерь для полосковых волноводов с воздушным заполнителем (1.10) находим, что в случае заполнения полосковых волноводов диэлектриком потери в них возрастут в в V-XX

... В полосковых волноводах, как и в других системах колебаниями вида ТЕМ, затухаше обусловлено потерями в токонесущих полосках и~аземленных пласти-на х, так как они не являются идеальными проводннка-

~ми, (потери проводимости), и потерями, вносимыми диэлектриком (диэлектрические потери). Потери проводи-мости для полосковых волноводов зависят от распределения тока в проводниках и удельной проводимости их у. Диэлектрические потери обычно определяются тангенсом угла диэлектрических потерь или величиной, обратной добротности 1/Q . мерой этих потерь является соотношение между полем в диэлектрике и полем в воздухе.

Затухание волн (Нп/м) в полосковых волноводах, заполненных диэлектриком, обусловленное потерями в по-лосках и заземленных пластинах, найдем из условий

Затухание волны (дБ/м) вследствие потерь в ди-элект ике определяется формулой [51]

27,3 К

где %-длина волны (м). 76

неограниченном пространстве

Обычно потери в полосковых волноводах малы, что позволяет выразить полное затухание как сумму всех видов затуханий [27]:

Таким образом, анализ экспериментальных данных показал, что для расчета полосковых волноводов с воздушным и твердым заполнителем можнб использовать одни и те же формулы.

§ 1.9. Несимметричный полосковый волновод как элемент СВЧ интегральных схем

Увеличение быстродействия радиоэлектронной аппаратуры привело к повышению рабочих частот вплоть до СВЧ. Длина волны при таких частотах становится одного порядка и меньше, чем протяженность элементов интегральных схем. Электромагнитное поле в схеме СВЧ диапазона не является- квазистационарным, как это имеет место на низких частотах, а проявляется в виде распространяющихся электромагнитных волн. Все элементы схемы оказываются связанными между собой быстропеременпым электромагнитным полем через окружающую среду.

Несимметричный полосковый волновод является наиболее распространенным элементом СВЧ интегральной схемы. При наличии диэлектрика размеры полосковых волноводов уменьшаются по сравнению с полосковымн волноводами с воздушным заполнителем. Ширина токонесущих полосок полосковых волноводов с твердым диэлектриком уменьшается, размеры волноводов становятся более критичны, затухание увеличивается.

СВЧ интегральные схемы предъявляют более жесткие требования как к применяемым материалам диэлектрических подложек (улучшению однородности и толщины диэлектрического листа' подложки, улучшению качества диэлектрика), так и к точности теоретических данных, пригодных для проектирования СВЧ интегральных схем.

Прежде всего это касается несимметричного полоскового ватновода на диэлектрических подложках как более распространенного элемента СВЧ интегральной схемы. Диэлектрические подложки имеют допуски на толщину и степень неоднородности листа, диэлектрнче-

екая проницаемость подложки также имеет некоторую нестабильность. Все это влияет в первую очередь на изменение характеристического сопротивления несимметричного полоскового волновода, которое достигает примерно ±5... 7%. Формула (1.105) для характеристического сопротивления несимметричного полоскового волновода, заполненного диэлектриком, которая получена ранее [41], может быть применена и для СВЧ интегральных схем. После незначительного уточнения она принимает вид

-, (1.107)

где е - относительная диэлектрическая проницаемость подложки.

Формула (1.107) пригодна для расчета характеристического сопротивления волноводов как с широкими токонесущими полосками (b!d>2), так и с узкими {b/d< <2). Она предельно проста, достаточно точна в большом интервале значений отношения bjd.

Из формулы (1.107) легко найти отношение bfd по заданным значениям характеристического сопротивления, которое может быть полезно при машинном проектировании:

6 =J-1. Z Vs

Преимущество машинного проектирования СВЧ интегральных схем состоит в быстроте расчета вариантов схемы и выборе оптимального. Задаваясь различными исходными величинами bjd; Afd; е и другими, легко находим зависимости С, Z, Рг, Р j. и Р от Ш, A/d н т. д.. необходимые при проектировании схемы.

В работе (128) Уилер предложил две формулы для вычисления харастернстичеокого сопротнвлен'ия несийметричного патоскового волновода, заполненного диэлектриком. Одна из них применима для волновода с широкими токонесушимн полосками (b/d>2), другая с узкими (Ь/й<2). Обе формулы весьма громоздки и требуют много времени для определения характеристического сопротивления (не пр-и-ведены к виду, удобному для практических расчетов).

На рис. (1.28 показаны кривые хараст-еристических сопротивлений несимметричных полосковых волноводов с различными диэлектриками, рассчитанные по формулам Уилера (сплошные кривые). На этом же рисунке пуиктирнымц .тиииями нанесены значения сопротивлений, определенных по формуле (1.107). Как видно из рнс. 1.28. результаты расчетов совпадают.

Если при определений Характеристического сопротивления несимметричного полоскового волновода, западненного твердым диэлестри-ком, появится необходимость учесть толщину токонесущей полоски А, то для отношений fc/d<2 необходимо пользоваться формулой

Z = -

(1 -I- hll) V е а для отнсмиений bld>2 - формулой

=-(l-A/d).

= /[+-т(т^)

(I.I08)

(1.109)

На-пример. в рпГшгс Dinuiiii несимметричный полосковый

волновод, зalloлIlenИ(Jй ли i.ic.hrpiiKOM с относительной диэлектрической про1шцасмостьм ь=К1 (AbO.i). Ширина токонесущей полоски 6=0,475; толщина ее Д=6,25 .мкм; толщина диэлектрической подложки d~fd мм (металлизирована только одна сторона). Характеристическое сопротивление волновода Z=SO,flO Ом.

Z,Oh

8 6/d

Рис. 1.28. Характеристическое сопротивление несимметричного полоскового волновода при различных значениях диэлектрической проницаемости заполнителя.

Найдем характеристическое сопротивление oio формуле (ЫОЗ) для отношений fc/rf<2. так как из примера следует, что b\d~ =0,475/0=0,95:

Z-.,.. .,- (1-Л/.) =

(li+b/d)K е

(1-1-0,95)1710 Погрешность 0,7 /о.

(1 -6,25.10-/0,5) = 50,36 Ом.

Рис. 1.29. Зависимости эффективной диэлектрической гроиицаемости от геометрии несимметричного полоскового волновода.

Как видно из примера и рис. 1.28, формулы (1.107) - (1.109) позволяют точно рассчитывать схемы СВЧ на несимметричных полосковых волноводах на различных диэлектрических подложках.

Формулу (1.107) можно использовать не только в СВЧ интегральных схемах-она хорошо реализуется для широких токопроводящих полосок несимметричных полосковых волноводов, заполненных диэлектриком.

Емкость на единицу длины (пФ/см) несимметрично-полоскового волновода, заполненного диэлектриком, с учетом толщины токонесущей полоски определяется по формулам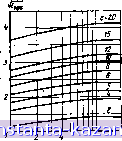

е S 10 да

C = 0,106.1ii

для b/d<2;

С = 0,106е

Уменьшение размеров несимметричных полосковых волноводов, применяемых в СВЧ интегральных схемах, требует чтобы при определении их геометрических размеров учитывалась величина эффективной диэлектрической проницаемости подложки еэфф- Величина еэфф служит мерой степени интеграции и уменьшения размеров [89]. Для узкой токонесущей полоски {b/d]) [46]

= -tin i 1.085--jiB/2-e-Еэфф=1.-Ь(1 Н-6)--

(1.110)

где B = Arch(4d/6).

Для широкой токонесущей полоски (bjdl) аналитическое выражение для эффективной диэлектрической проницаемости весьма громоздко, поэтому занисимость Еэфф от отношения bjd представлена графически (рис. 1.29). 80

§ Расчет электрических параметров полосковых волноводов

Пример (1. Рассчитать параметры несимметричного полоскового волновода с воздушным заполнителем.

Дано: длина волны в несимметричном волноводе Я=5 см; ширина токонесущей лолоски h 5 мм; расстояние между токонесущей полоской и заземленной пл.-ктииоп = I m*i; токонесущая -полоска м заземленная пластина выпоШспы лз меди.

1. Емкость иа единицу дл......1 несимметричного полоскового волновода. 2. Характерист1гчсское сопротивление несимметричного полоскового волновода. ,Ч. MuKcnMa.iuiiu допустимую мощность, которую можно передать чецс! попсрсню!- L-eiiuiuie несимметричного полоскового олновода. Ч IIiiR-rif н несимметричном полосковом волноводе. 5. Затухание.

Решение:

1. Емкость на е-дяницу длины определяем ио формуле (11.92):

С=0 106(1 -t-b/d)=0jl06(l-I-S) =0j636 пФ/см.

2. Характеристическое сопротивление определяем -то формуле (1.98)

Z-300/(l-t-ft/d)=300/(l-(-5)=50 Ом.

3. Макетмальио допустимую мощность, которую можно передать по несимметричному полосковому волноводу, находим по формуле (1.16)

Ямввс=9,5-10 йг/в = 9.5-10 (110-)2-11,3=10.7-10= Вт=10,7 кВг.

Значение Гв для отношения ft/d=S, находим .по таблице, приведенной в.Приложении 2. £0=1,06-10 В/м.

(Мощность пробоя несимметричного толоскового волновода равна

P p-4,22.10-£2pdV£ = = 4,22-10-*(3.10 )2(1-Ш- )> 11,3=43 кВт,

где Е„р=3.40 В/м.

4. Максимальные потери в несимметричном полосковом волноводе рассчитываются по фор.муле (1.10)

Pj ,=2,23-10- -KEld X (Аге-l) (А'А- )

(А-вЧ-1)4°=/4

=2,52-1С . 2-10-!-1-10--17.7=894 Вт,

где поверхностное сопротивление в = )/ Д' ЗДи равно S = = 8,25-10-= Y\ [ГГц] Ом. На частоте f=6 ГГц (>. = 5 см) R = = 8,25-10-К^з^г-Ш-! Ом.

6-792 81