полноводе с твердим ли электриком. ЦептральпыП проводник образован отре.мчом однородного волновода 1 и неоднородного 2 с диэлектриком из поликристаллического феррита 3. Пересi-jioiiKa осуществляется изменением на-пряжеппостн имсшнего магнитного поля Н. Связь с источником М(нцм11стн 6 и нагрузкой 7 осуществляется через элеменгы сиял] 5 к 4 соответственно. Параметры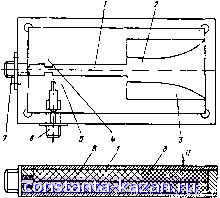

Рис. 2.1. Перестраиваемый резонатор па симметричном полосковом волноводе.

связи подобраны таким образом, что в диапазоне перестройки удовлетворяют критерию постоянства нагруженной добротности Qn.

Независимо от вида резонатора его роль в СВЧ устройстве сводится в основном к получению требуемого значения резонансной частоты, определенной величины добротности и резонансного сопротивления.

В общем случае существует два способа соединения резонатора с внешней схемой:

1) резонатор включен по схеме двухполюсника, при этом нагрузка подключается параллельно или последовательно с активным элементом (рис. 2.2,а);

2) резонатор включен по схеме четырехполюсника, при этом нагрузка и активный элемент могут подклю-

чаться различными способами, в том числе и распределенной связью (рис. 2.2,(;).

Для общности рассуждений под активным элементом понимаем двухполюсник, отдающий энергию (фидер приемной антенны, тнордитсльный активный элемент, выходная цепь усилители и т, %). под нагрузкой-- двухполюсник, поглощающий энергию, (вход смесителя, индикаторная цепь волномера и т. д.).

Кг(01

Pin-. 2.2. Фуикцнопальчые схемы одноконтурного генератора с актив-HidM WK-MemiiM, иклшченным мо схеме чстырехнолюсника (а) и двух-110Л[>сП11Ка

На этих рисунках связь между резонатором и внешней схемйй представлена в виде идеальных трансформаторов сопротивлений с коэффициентами трансформации Х(со), определяемыми степенью связи и частотой.

Такое представлеппе широко применяется в технике СВЧ [87] н нытскаег нз теоремы Вайсфлоха об эквивалентном трансформаторе (69]. Следует отметить, что коэффициент трансформации сопротивлений К (со) связан с коэффициентом трансформации идеального трансформатора п зависимостью К(й))=п^. Параметры связи р для рис. 2.2,6 (как более общего случая) будут равны:

(2.1)

j5, = Ki(<o)/?r/>;

Р2=/С2(№)/?н -,

(2.2)

где -внутреннее сопротивление активного элемента на входных зажимах трансформатора Тр1\ г - эквивалентное последовательное сопротивление потерь резона-

тора; Rb - сопротиплсние нагрузки на входных зажимах трансформатора Тр2.

Параметр сннзн характеризует эффективность передачи в сонрогннленне нагрузки и активного элемента энергии, 3iiH;KciHH)ii в резонаторе. Добротность нагруженного pcionaropii Qn выражается через параметры связи и ненагружснную добротность Qo следующим образом [10]:

Q.i=Qo/(l-bPi-bp2). (2.3)

Активный элемент

Резотшюр

Нагрцзиа

Рпс. 2.3. Эквивалентные схе.мь! одноконтурного генератора с активным элементом: включенным по схеме двухполюсника (б) и четырехполюсника (с).

В зависимости от вида элемента связи и его конкретного выполнения трансформатор сопротивлений может быть повышающим - К(м)>1, понижающим - К( )<1 или отсутствовать при прямом соединении. Параметры такого трансформатора, т. е. коэффициент трансформации сопротивлений, его зависимость от частоты, а также положение'зажимов могут быть определены экспериментально при любой структуре неоднородности в волноводе, образующей трансформирующую секцию; существенно лишь отсутствие в неоднородности заметных активных потерь. Во многих практических случаях эти параметры можно определить, применяя аналитические и графические методы вычислений. Представление четырехполюсника связи в виде эквивалентного трансформатора сопротивлений позволяет упростить расчет резонаторов, и в первую очередь колебательных систем генераторов на твердотельных активных элементах, так как последние обладают сравнительно низкой собственной добротностью и для получения максимальной мощности их приходится сильно связывать с нагрузкой. В резуль-90

тате элемент связи составляет заметную часть колебательной системы, что сун1естпенно затрудняет ее расчет, а тем более синтез по заданным характеристикам. Представление элементов связи трансформаторами сопротивлений позволяет отдельно рассчитать ненагруженный резонатор, а затем с учетом 1н)лученных характеристик рассчитать параметры трансформаторов сопротивлений, обеспечивающие оптимальную связь активного элемента с нагрузкой и резонатором.

§ 2.2. Расчет pcjuiiaiopon на полосконых волноводах

Расчет резонатора рассмотрен на примере колебательной системы Одноконтурного генератора. Отметим, что расчет такой системы не отличается принципиально от расчета, например, резонансной детекторной головки или смесителя при условии, что понятие активного элемента и нагрузки соответствует принятому ранее.

Во многих случаях резонатор связывается с активным элементом непосредственно, т. е. трансформатор сопротивлений Тр1 (рис. 2.2) отсутствует и эквивалентные схемы одноконтурных генераторов имеют вид, представленный на рнс. 2.3.

На этих рисунках гп(со) =/? [К(ш)]-приведенное сопротивление нагрузки иа зажимах трансформатора сопротивлений. Величина и зависимость от частоты этого сопротивления определяются трансформатором сопротивлений, параметры которого в свою очередь зависят от способа связи с нагрузкой. Ненагруженная резонансная система образуется сосредоточенной емкостью Со и индуктивностью замкнутого или разомкнутого отрезка полоскового волновода с характеристическим сопротивлением Zp. Величина емкости Со и параллельно соединенного отрицательного сопротивления - R определяется видом активного элемента. Можно отметить, что резонатор, представленный на рис. 2.3,6, образован отрезком замкнутого, если r (co)<Zp, и разомкнутого, если ги(со) 3>Zp, полоскового волновода.

В конечном счете можно представить ненагружеииую резонансную систему независимо от способа соединения ее с активным элементом и нагрузкой в виде отрезка волновода, нагруженного емкостью Со (рис. 2.4). Здесь г„ - эквивалентное последовательное сопротивление активных потерь в резонаторе, отнесенное ко входу от-

резка, а /р-релотшспая длина отрезка, обеспечивающая резонанс с смьосгью Со.

Основные элскгрпческие характеристики такой полу-распределенной системы, как и колебательной системы на сосрсдоточс.....>ix постоянных, вблизи резонансной частоты оннсываюгся одними и теми же параметрами: резонансной часгогой (Ос, эквивалентными резонансными сопротнвлснннмн н г^ири 1ар.эллельиом и последовательном резонансе соответственно, а также собственной (ненагруженной) добротностью Qo.

Ilic. 2.4. Эквивалентная схема jieaSTPYeHHoft резонансной системы па :;амкнутом (а) п разомкнутом (б) отрезках волновода.

Подчеркнем, что указанные параметры полностью характеризуют поведение резонатора только на резонансной частоте (в пределах полосы пропускания) и выбранном типе колебаний [57].

В зависимости от механизма образования отрицательного сопротивления активные элементы подразделяют иа: 1) устойчивые при jaKHVTOU внешней цепи (например туннельный диод) и 2) устойчивые при разо-мкнутой внешней цепи (например лавинио-пролётный диодТГ

В первом случае активный элемент представляется в виде отрицательного сопротивления -Л, шунтированного реактивностью, например емкостью перехода Со. Резонансная система подключается параллельно отрицательному сопротивлению и характеризуется эквивалентным резонансным сопротивлением Яоэ- Для возникновения генерации необходимо, чтобы Коэ^\-R\ \ (рис. 2.5,а). Зависимость R оэ от частоты соответствует характеристике параллельного резонансного контура. Во втором случае активный элемент представляется в виде отрицательного сопротивления -г, соединенного последовательно с реактивностью, например емкостью перехода Со. Резонансная система включается последова-92

тельно с отрицательным сопротивлением н характеризуется эквивалентным резонансным сопротивлением Гоэ-Для возникновения генерации необходимо, чтобы Гоа^ ОХ 1-I (рис. 2.5,6). Зависимость Гоэ от частоты соот- --- ветствует характеристике последовательного колебательного контура.

Рнс 2.5. Эквивалентная схема генератора с активным элементом, устойчивым при замкнутой внешней цепи (а) и при разомкнутой (б).

Резонансная частота. На этой частоте в резонаторе устанавливается стоячая волна (кроме так называемых резонаторов бегущей волны, которые мы не рассматриваем). Иначе говоря, условием резонанса является синфазное сложение волн в любом сечении полоскового волновода, образующего резонатор, тогда реактивная проводимость (сопротивление) в любом сечении резонатора равна нулю. Поэтому резонансную частоту Юо определим из условия равенства входного сопротивления ко-роткозамкнутого или разомкнутбго отрезка полоскового волновода емкостному сопротивлению емкости Со:

j;=ZptgW короткозамкнутый.

\ ° (2.4)

- = ZfCtgkl разомкнутый.

Здесь k=2n/X - волновое число; Zp - характеристическое сопротивление полоскового волновода!

Так как резонансная длина волны X и длина отрезка /р однозначно связаны, то для короткозамкнутого или разомкнутого отрезка волновода можно соответственно получить:

Здесь п=0, 1, 2 см; Со пФ.

(2.5)