- при расположении ее в центре (рис. 1.2,6) характеристики будут как у волновода, изображенного на рис. 1,1,г; потери возрастают незначительно, но изготовление упрощается;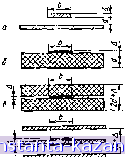

Рис. 1.1. Конструкции полосковых волноводов;

а - несимметричный с воздушным заполнением; б - несимметричный с твердым диэлектриком; в - симметричный с твердым диэлектриком; г-симметричный с воздушным заполнением и токонесущей полоской, нанесенной с двух сторон опорной диэлектрической пластины.

Рис. 1.2. Симметричный полосковый волновод с воздушным заполнением (а) и волноводы с пояложкон, подвешенной симметрично (6), несимметрично (в).

- при расположении токонесущей полоски на небольшом расстоянии от заземленной пластины (рис. 1.2,в) характеристики приближаются к характеристикам волновода, показанного на рис. 1.1,а. Воздушный зазор под диэлектрической пластиной существенно уменьшает эффективную диэлектрическую проницаемость и соответственно диэлектрические потери, кроме того при наличии зазора снижаются требования к допускам на параметры диэлектрика.

§ 1.1. Справедливость метода ТЕМ волны для расчета полосковых волноводов

Основной задачей при расчете полосковых волноводов является нахождение структуры поля. Направим ось г прямоугольной системы координат вдоль полос-10

нового волновода. Электромагнитное поле полосковых вадноводов проще всего рассчитать при помощи векторного электрического потенциала А.

Векторный электрический потенциал удовлетворяет . векторному волновому уравнению

дЛ + АМ = 0,

где й=2лД-волновое число ли постоянная распространения волны в неограниченной среде; Я - длина волны в яеограниченной среде; А - оператор Лапласа (или лапласиан) обозначает сумму вторых частных Производных по трем координатным осям.

Для магнитного поля всегда имеет место соотношение

H = TOtA; А

bdv.

где 8 - вектор плотности тока проводимости.

В полосковых волноводах токи проводимости в токонесущей полоске и заземленных проводящих пластинах значительно превышают токи смещения, и, следователь- но, последними можно пренебречь. В таком случае магнитные силовые линии будут охватывать ток проводимости и вектор плотности тока проводимости будет полностью определять вихрь магнитного поля.

Поскольку мы рассматриваем ТЕМ волну, то вектор плотности тока проводимости должен иметь одну составляющую, направленную вдоль полоскового волновода по оси Z, так что 6i=6 =0, б^фО. Отсюда следует, что и векторный потенциал имеет одну составляющую (только по оси г) А^=Ау = 0\ АгФО, т. е. векторный потенциал во всех точках пространства, окружающего полосковый волновод, имеет то же направление, что и г-я составляющая вектора плотности тока 6z. В этом случае магнитные силовые линии охватывают ток проводимости 6, и токонесущую полоску (проводящие пластины заземлены).

В ТЕМ волне линии равного потока электрического поля лежат в плоскости поперечного сечения полоскового волновода и электрическое поле не имеет продольной составляющей. Линии равного потока должны начинаться и заканчиваться на основной проводящей полоске и заземленных пластинах полоскового волновода. Отсюда

И

следует, что электрическое 1[ магнитное поля связаны с геометрией полосковых волноводов. Эта связь обусловливает направление распространения энергии вдоль полосковых волноводов, как это имеет место в системах с ТЕМ волной.

Из картин распределения поля для несимметричных полосковых волноводов различной геометрии, .получен-кых автором в электролитической ванне (рис. 1.3), вид-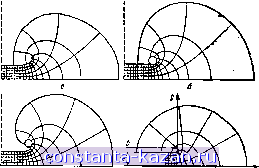

Рис. 1.3. Картины поля в поперечном сечении несимметричных полосковых волноводов:

о - изгиб токонесущей полоски по лмнин Равного потенциала; б -трубчатые концы токонесущей полоски; в - изгиб токонесущей полоски с трубчатыми концами по линии равного потенциала; г -модель нсследгсмого волновода.

но, ЧТО В несимметричных полосковых волноводах, так же как и в симметричных, магнитные силовые линии охватывают проводящую полоску, по которой течет ток проводимости. Теория и эксперимент подтверждают, что поле концентрируется в области полосок. Волновое уравнение для Аг принимает скалярный вид ЛЛг-1-йМзг=0 и выполняется во всех точках среды, окружающей патос-ковые волноводы (исключая точки самой поверхности проводящих полосок и заземленных пластин полосковых волноводов). Решение этого уравнения надо искать в виде бегущей волны, изменяющейся во времени по гармоническому закону и распространяющейся вдоль положительного направления оси 2. 12

Напишем в самом общем виде волновое уравнеягие для составляющей векторного потенциала для полоскового волновода

где a=t.-jp - комплексная постоянная распространения волны в полосковом волноводе; £ - фазовая постоянная; р - постоянная затухания.

Если положительна, то волна распространяется в направлении возрастания координаты г.

Поле будет распространяться вдоль полоскового волновода в виде волны с амплитудой, зависящей от х и (/. По физическому смыслу а является волновым числом или постоянной распространения в полосковом волноводе: а=2лДш где Хпв - длина волны в полосковом волноводе.

Длина волны в несимметричном полосковом волноводе, заполненном диэлектриком, при распространении квази-ТЕМ волны задается выражением

где А - длина волны в неограниченном пространстве; ввфф - эффективная диэлектрическая проницаемость.

Решить волновое уравнение для полосковых волноводов, заполненных диэлектриком, найти вид спектра, т. е. значения величин й^-щг д структуру волн в поперечном сечении полосковых волноводов - весьма трудная математическая задача, так как при распространении квази-ТЕМ волны в несимметричном полосковом волноводе, заполненном диэлектриком, силовые линии электрического поля проходят не только в диэлектрике, но и в воздухе.

Для полоскового волновода с воздушным заполнителем эффективная диэлектрическая проницаемость еэфф= 1 и длина волны в волноводе равна длине волны в неограниченном пространстве. Таким образом, фазовая скорость и скорость распространения волны в несимметрич-HOJI полосковом волноводе с воздушным заполнителем совпадают со скоростью распространения волны в не-. ограниченном пространстве.

В работах {117, 130] дан гармонический анализ условий распространения волн в несимметричных полооковых волноводах, коробчатой конструкции (рис. 1.4).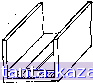

Рис. 1.4. Конструкция коробчатого полоскового волновода.

Установлено, что длина волны в несимметричном полос-ковом волноводе, вычисленная в предположении распространения нелиспергярующей ТЕМ волны, на частоте 10 ГГц может превышать истинное значение на 5%,.

а в диапазоне 2 ... 3 ГГц и ниже практически совпадает с ним [84]..

Учитывая сказанное, можно положить k=a. Тогда поле не будет иметь продольных составляющих т. е. вект оры поля будут лежать, в плоскости поперечногоТёчения полоскового волновода и само поле станет поперечным. В этом случае для дальнейших исследований можно использовать ТЕМ волну, что даст результаты, точность которых достаточна для инженерной практики.

При 2 = а^ в илоскости поперечного сечения полоскового волновода поле удовлетворяет уравнению Лапласа, т. е. оно имеет такую же структуру, как и в электростатическом случае: д^Аг1дх+д^А^ду=0. Из условия diV/4=-ЕаРайф/Л, связывающего векторный потенциал А со скалярным р, для нашего случая имеем

div А = бЛг/йг=-jaA z=-ЕаЦаЗч>/Л. После Интегрирования по времени получаем

где 2=l/Ha/a - волновое сопротивление волны ТЕМ; Лг - составляющая векторного потенциала по. оси г; ф - скалярный потенциал.

По векторному или скалярному потенциалу можно определить напряженность электрогиа гвитиого поля в по-лосковом волноводе:

£=-gradf; Я = го1Л.

Из теории длинных линий известно, что для волны, распространяющейся в положительном направлении оси г, отношение напряжения и тока а каждой точке равно волново!йу сопротивлению:

UjI = Z = YLlC,

Где L - погонная индуктивность линии, t/м; С - погонная емкость линии, Ф/м. Волновод, сопротивление^ и в данном случае не зависит от координаты z и ка1Г ха-рактеристический параметр линии определяет отношение напряжения к току бегущей волны в любой точке линий.

В СВЧ линиях понятия напряжения и тока играют второстепенную роль. Основным является понятие электромагнитного поля, в частности распределение поля в поперечном сечении линии. Волновое сопротивление поля определяется уравнением 2=ЕтЩт, где £т и Нт - напряженности электрического и магнитного поперечного поля волны, распространяющейся в положительном направлении оси z. Это определение имеет смысл, так как величина Z в поперечном сечении постоянна. При отсутствии потерь волновое сопротивление Z вещественно.

Параметр линии Z часто называют характеристическим сопротивлением, реже характеристическим импедансом линии. По отношению к полосковым волноводам величину Z будем называть характеристическим сопро-

Приближениые условия существования волн типа

ТЕМ в полосковых волноводах могут быть обеспечены, если электрическая ширина токонесущей полоски и расстояние между ней и заземленной пластиной меньше половицы длины волны в волнов оде, При этих условиях электрическое и магнитное поля в основном сосредоточены между полоской и заземленной пластиной и их можно рассматривать раздельно.

Рассматриваемое поперечное поле (в смысле его связи с проводящими поверхностями полоскового волновода) имеет такое же распределение, как и в электростатическом случае, и может быть описано уравнением Лапласа. В электростатике скалярный потенциал удовлетворяет уравнению Лапласа л^ф-О и на поверхностях проводящих полосок принимает значения qn и фг. По скалярному потенциалу определяется напряженность электрического поля полоскового волновода Е=-gradф, по найденному распределению поля - остальные его электрические параметры.

Таким образом, при рассмотрении ТЕМ волнымож-ио использовать уравнения электростатики в плоскости поперечного сечения полоскового волновода с воздушным заполнителем. -