на частоте fa, определяемое выражением

2 = Z .

./Kl-(я/я p)

где Zn .=(j0ji6/2 - характеристическое сопротивление прямоугольного волновода на бесконечной частоте.

Последующий расчет геометрических размеров согласующих ступенек выполняется но известной методике расчета ступенчатых переходов 193]. Значение длины волны для каждой ступеньки, необходимое для расчета ее продольного размера, определяется по формуле

где Xino - длина волны в П-образном волноводе; X - расчетная длина волиы.

§ 6.2. Расчет перехода

Рассчитаем переход с прямоугольного волновода сечением 35X5 мм на несимметричный полосковый волновод с ха.ра твристиче-ским сопротивлением 2, -50 Ом на диэлектрике толщиной d= = 2 мм. Диапазон частот согласования 5300 ... 6500 ГГц; максимальный коэффициент отражения по

as as 0,7 D.9 ф

Рис. 6.6. Зависимость характеристического сопротивления П-образиого волновода от размеров ступенек.

модулю Г|макс =0,05.

Используя формулы (6.1) - (6.5) и номограммы- (рис. 6.4), строим зависимость Zno(S/fl) (рис. 6.5). Точка пересечения дает значение ширины гребия S = = 12,9 мм.

Следует отметить, что иа этом графике можно не только решить задачу согласования сопротивлений, но и получить одинаковую ширину полоски и гребня. Для этого на рис. 6.5 наносится зависимость Zmu=-I{bnn), где Ьшп -

ширина токонесущей полоски несимметричного полоскового волновода. Точка пересечения кривых Z (S/a) и 2 =ДЬн„) дает значение Zn=Z и S=f)a . Но

здесь -может потребоваться еще дополнительный переход между соответствующими сечениями полоскового волновода.

Определив параметры исходного П-образного волновода, строим зависимость Zno(d/b) (рис. 6.6).

Находим перепад характеристических сопротивлений R = -Z /Z =U23/50=2.5.

Средняя длина волиы диапазона согласования

Хо= (> . и-1-Яи.кс)/2=1(4,€-(-5,67)/2=5,1 см. Средняя длина волиы в прямоугольном волноводе

К, = K/i - (оДй) 1-(5,1/7,0)= =7.45 см.

Средняя длина иолны в П-образном волноводе Km = KV l-(>..A.pm)5,1/Kl-(5,1/8,1)= = 6,6 см.

Длина волиы в П-образном волноводе на нижней частоте диапЭ' зона согласования

W = 1 -( сЛ.Рго)= = 5,67/Kl -(5,67/8,1)=7.85 см.

Длина волиы в прямоугольном волноводе на верхней частоте диапазона согласования

К = K/V 1 - (), я./2а) =4,6 1 -(4.6/7) = 6,13 см. Диалз.зон перекрытия ?,и., с noAvnii 11 = 7,86/6,13= 1,28=4,3.

Так как .диапазон перекрытия небольшой, выбираем переход с максимально плоской характеристикой как обладающий достаточно линейной частотно-фазовой характеристикой. При это,м активная составляющая входного солротивлевия в полосе пропускания близка к постоянной величине, а реактивная равна нулю.

По табл. 6.1 для полученных значений R - 2,5; Я, ане по/мин п = = 1,3 и заданного 1Г|макс=0,05, интерполируя, находим число ступенек п-2.

Аналогично находим (табл. 6.2) дли /?=2,5 и n=2 иормнровап-иые характеристические сопротивления ступенек: р, = 1,25; р2=1,98.

Характеристические сопротивления ступенек П-образного волновода (рис. 6.6)

Z o,=Z p,=50-1,25 = 62,6 Ом; Z K=2 Dp2=50-1,98 = 99 Ом.

По графику рис. 6.6 находим соответствующие значения

d!=2,62 wm; d, = 4,S мм.

Длины воля в П-образном волноводе при найденных размерах ступенек

V 1 -(>. /Wro)== 5.1 /1- (5.1/7.3) = М-) : I ;

i o = >.D V{ -(Л.,р, о) =: 5,1/>1 -(5,1 -7,05) = 7,45 см.

где Хкр2по=7,3 см и Якр1по=7,05 см-критические длины волн П-об-раэпого волновода при данных раэ.мерах ds и di. Нескорректированные длины ступенек

/а=Хгло/4=7,15/4=1,79 см; Л =(?,i /4=7.45/4 = 1.86 см.

Произведем коррекцию длины только первой ступеньки, так как высота второй ступеньки незначительна:

(j=(j-4=11,79-0,05=11,74 см,

где

Л=(2(2 ... 3)% = 1.79(2 ... 3)/100==0,05 см.

Д11П1У выходной секции П-оброзиого волновода Лто примем раеиой 2 см. Таким образом, размеры ступенчатого перехода определены.

ТАБЛИЦА 6.1

n = 2

n = 3

n = 4

Коэффициент отражения г

0,02

0,05

0.02

0,05

0,02

0,05

1.г

1.4 1,6 1.8

2,0 2,2 2,4 2,6 2,8 3,0 3.2 3,4 3,6 3,8 4.0 4.2 4,4 4.6 4,8 5.0 5.2

2,389 1,874 1.692 1,601 1,538 1,494 1,457 1,427 1,415 1,398 1,384 1.372 1,361 1,350 1,342 1.334 1,326 1,320 1,315 1,309 1,304

4,510

2,795

2,344

2,125

1,994

1,903

1,837-

1.786

1,743

1.710

1,681

1,656

1,635

1,614

1,597

1,584

1,571

1,558

1.544

1,535

1,525

4,952 3,566 3,024 2,731 2.540 2.401 2.300 2,226 2,160 2,106 2,058 2,021 1,985 1,954 1,928 1,903 1,882 1.861 1.845 1.829

3,651 2,831 2,484 2,317 2,210 2,130 2,072 0,026 1.985 * 1,950 1,920 1,894 1,874 1,853 1,833 1.821 1,809 1,793 1,786 1,770 1,762

7,000 4,305 3,598 3,228 2,976 2,854 2,731 2,643 2,571 2,515 2,460 2,413 2,407 2,344 2,310 2,289 2,267 2,241 2,220 2,205 2,185

7,658 5,601 4,682 4,233 3,914 3,728 3,525 3,386 3,274 3,193 3.107 3,048 2,992 2,937 2,891 2.854 2,810 2,774 2,745 2,710

4,996 3,804 3,370 3,123 2,952 2,850 2,763 2,701 2,641 2,587 2,550 2,507 2,483 2,456 2,430 2,408 2.382 2,364 2,346 2,332

9.579 5,875 4,917 4,399 4,092 3,871 3,710 3,586 3,469 3,400 3,340 3,316 3,223 3,173 3,118 3,075 3,049 3,018 2,982 2.957

5,786 5,322 5,042 4,807 4,621 4,474 4,353 4,245 4,151 4.076 3,995 3,940 3,879 3.826 3,782 3,732

ТАБЛИЦА 6.2

Рис. 6.7. Эскиз коаксиальио-по-лоскового перехода акспалыюго типа.

§ 6.3. Ко:1Нсиа.лыш-ПоЛосковые переходы

В технике iiojHitKOBMX волноводов широко используются коаксннльно-полосковые переходы. Их основным параметром нвляотся коэффициент стоячей волны на входе, .\аракпч)пзующий уровень отражений от перехода в полосе частот. Чем резче выражен характер ; неоднородности в месте

соединения разнородных волноводов, тем выше КСВН и уже рабочий диапазон частот. При согласовании в узком диапазоне частот проще всего согласовать переход, подключив к тракту одну или две регулируемых реактивности. При необходимости же согласования в широкой полосе частот приходится принимать меры к уменьшению величины неоднородностисты-ка путем плавного изменения его структуры ипр.

Коакснально - полосковые переходы разделяются на аксиальные (торцевые) и перпендикулярные. В первом случае оси коаксиала и полоскового волновода совпадают или параллельны Рис. 6.8. Аксиальный переход друг другу, а ВО втором- с трансформирующей секцией (о) перпендикулярны.

и коаксиально-полосковыи пере- f .

ход (6) . Наиболее распростра-

S :;5ненная конструкция аксиального перехода показана на рис. 6.7. КСВН такого перехода менее 1,05 в полосе длин волн от 2,7 до 19 6 (6 - ширина токонесущей пмоски), что говорит о хорошем качестве перехода [91]. Если же требуется меньший уровень отражений, применяют переходы с трансформацией поперечного сечения, изображенные на рнс. 6.8,а. В этих переходах поперечное сечение коакспального волновода носгепеино трансформируется в поперечное се-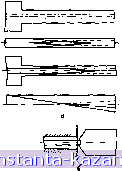

чение Полоскового волновода. Чем длиннее учасгок трансформации, тем меньше отражения от перехода. Обычно длина участка трансформации составляет несколько длин волн. .-)г() обстоятельство часто бывает нежелательным нз-аа гроит.чдкостн устройства, поэтому переходы с трансформацнсп мало распространены. В слу-

Центральный проЫник полоскового волновода

80 I

60

Рис. 6.9. Номограмма для расчета переходов аксиального типа.

чае, когда ограничения на параметры перехода менее жестки, можно применять переход,описанный в {105]. Конструкция перехода показана на рис. 6.8,6. Такой переход имеет КСВН менее 1,Г5 в 17%-иой полосе частот (на центральной частоте 600 МГц) и вносимых потерях менее 0,4 дБ.

12-792 177