§ 1.2. Расчет поля в несимметричном полосковом волноводе с воз шным заполнителем

На рис. 1.5,0 показано поперечное сечение несимметричного полоскового волновода, где b - ширина токонесущей полоски; А -ее толщина; d -расстояние между полоской и заземленной пластиной. Для определения непередаваемой М01Ц110СТИ, потерь и затухания, в несимметричном полосковом волноводе необходимо знать jacnpe-деТГение поля £ свободном от проводящих поверхностей пространстве,

П/юЫисШЬ Z

Рис. 1.5, Конформное преобразование несимметричного полоскового волновода: /

а - поперечное сечение: б - по-следовяТЕЛЬность преобразова-ння

Плосиость W

Нас будет интересовать случай, когда объемная плотность зарядов везде равна нулю, за исключением проводящих поверхностей полоскового волновода. Для упрощения расчетов воспользуемся плоской симметрией, где

£ и ф зависят только от л: и у.

Определяя значения £ и ф, воспользуемся методом функций комплексного переменного. Между теорией функций и теорией потенциала существует тесная взаимосвязь. Для нашего случая эта связь может быть выражена следующим образом. 16

Если и + уо - произвольная аналитическая функция от zx+jy, где и, V, X и у - вещественные величины, то и ъ V удовлетворяют уравнению Лапласа и условиям Коши-Рнмана. Общ^ш.решение этого уравнения для нлоской зарачи и=Ке/(г), где f(z) может быть произвольной аналитической функцией, а вещественная часть /(2) будет вещественной частью функции в точках х, у.

Наша задача значительно упрощается, если применить конформное преобразование zf(w), отобразив плоскость Z ъ плоскости W (более подробно это изложено в Приложении 1). Перенесение законов конформного преобразования в теорию потенциала дает существенное преимущество перед попыткой непосредственного вычисления потенциала.

Расчет поля с учетом толщины токонесущей полоски произведем в комплексной плоскости, полученной путем конформного отображения. Вычислим электростатическое распределение для правой половины поперечного сечения полоскового волновода при допущении, что левая половина простирается до бесконечности. Электрическое распределение для левой половины получится из условий симметрии (рис. 1.5,6).

Для определения расчетных формул будем обходить проводящие поверхности полоскового волновода, как показано пунктиром на рис, 1.5,6, по контуру ABCDE. Ломаную линяю ABCDE с помощью формулы Кристоф-феля - Шварца переведем на две параллельные прямые с расстоянием л между птт.

Выпишем формулу Кристоффеля - Шварца для преобразования ломаной линии ABCDE в плоскости Z в вещественную ось плоскости W:

dzjdw =-----. (1.1)

Точку В плоскости Z с координатами 2i=j(d--A) переведем в точку Bi плоскости W с координатами Wi=-q (q требуется определить). Угол поворота в точке В при обходе контура ABCDE стремится к -л/2; яу1=-л/2, откуда Yi=-1/2. Точку С плоскости Z с координатами Z2=jd переведем в точку d плоскости W с координатами т^=-1. Угол поворота в точке С стремится к -л/2; яу2=-.тг/2, откуда 2=-1/2.

Точку D плоскости Z с координатами 2з=со переведем в точку Di плоскости W с координатами а)з=0. 2-792 17

Угол поворота в точке I) стремится к л; щзп, откуда При этих условиях формула (1.1) примет вид

z = C-V{w + q)(w+\)dm. (1.2)

Для решения интеграла (1.2) воспользуемся подстановкой Эйлера (w+q)(w + \)=P(w+q)\ Из последнего выражения находим

Подставляя значения т я dw ъ формулу (1,2), получаем

г-С f g.j. - J i}t)44t-

= 2С(9-1)Ч-г--- (1.3)

Подынтегральное выражение является правильной дробью, которую можно представить в виде суммы конечного числа простых дробей.

Для выполнения интегрирования разложим правильную дробь на простые, пользуясь методом неопределенных коэффициентов: А I А , А, i 1 л

- (1-044-04?-1)

где коэффициенты At...At подлежат определению.

Умножая обе части этого тождества на общий знаменатель дробей, получаем новое тождество

А,(\+ tf (qf 1) + Д( I - О (1 -f О' - 1) + + A,{\-t(ql-\) + A,(\+t){\tf(qt-\) + + Л.(1 - tf [tYq~\) + A,(\- ty (tYq+\) t.

Полагая <=-1; < = +1; <=-1/V7; t=4V7 находим, ijTO

л Д л д Я

-4( J) i- *в2( 1)2-

Приравняв коэффициенты при одинаковых степенях i, придем к системе уравнений

-qAz+qAi,=Q при V; Л1-Лг-Ла-Л4-1-Л5-Лб=0 при Л Из написанной системы легко найти.

А -А -Ji+iL

Подставляя значение найденных коэффициентов и интегрируя (1.3), получаем

in -f In 4+4-f

2 = CV

-1 (

1 -

(1.4)

где t=*\n.ti+l)l{w + qi . Находим постоянные С и С„

Известно, что показательная функция ги=е переводит полосу шириной d в верхнюю полуплоскость. При W, близких к нулю, dZfdw должно совпадать с dz/dw, т. е.

Ига rci> + >(- + Lf )1

QdT-Y Ц При т)=- 1 z = dj и i = 0. Из (1.4) получаем

dj = С К? [Ш (-1) + In (1) ] + С,.

Берем главную ветвь логарифма'с/]==- С

откуда С, = 0.

Подставляя значения С и С, в (1.4), находим

(1.5)

Подставив в выражение для t значение ш=с^, получим функцию, которая преобразует поле полоскового 2* 1

волновода с расстоянием между проводящими поверхностями d в известное поле идеального плоского конденсатора с расстоппием п между пластинами.

Для ВЫЧИСЛСГП1Я q имеем; г=](йЧ-Л); ш=-q\ t=oo.

Via (1.4) получим

d q+l

j(d + u) =

Реиия последнее выражение, найдем

q = - 1 + 2 (1 + u/d)4- 2 (1 + Д/d) /(T-f Д/d) - 1.

(1.6)

Рассмотрим случай, когда d > й. Тогда можно записать \ -\- i/d=l -\-а, где a - Cifd мало.

В этом случае (1.6) перепишется следующим образом: <7=-l + 2(l+<x)-j-2(l+a)/(l+a)=-l~ - 1 + 2+ 4 + <х гЛГ (21/2 +/2/2)+

где а=2/2а--4а---.- мало.

Подставим (7 =1-4-а в выражение для t:

t=y(w+\)!(w+q) = Y(w+ \)!{w+ 1 +а).

Разложим последнее выражение в ряд Маклорена

d/[2(t0 + 1)] + 3cVl8(ш +\f]~

- 15а'Д48 (да-1-1)] + .. .

Ограничимся, ввиду малости а, первыми тремя членами ряда. Подставим t(a) в (1.5). После преобразования получим

2 = -[(да+1) + 1п^--2-(и+1)]. (1.7) Переходя к плоскости окончательно имеем г=4-р+ 1 1.41 УШ(е^+ 1)- 2А(е^- 1)

(1.8)

Формулу (1.8) можно упростить: при малой толщине токонесущей полоски (A/d<0,2) последним слагаемым можно пренебречь, тогда

г=4[еЧ 1 +1: - 1,41 )/A/d(e4 1)1-]- (Щ

Из формулы (1.8а) легко получить параметрические уравнения для линий равного потока и равного потенциала:

A:=;lecos 7i-f E-f 1 - 1,41/A/decosTj- 1,41/Д/а1;

y=~[esmii + Ti- 1,41 /A/desimil.

По этим формулам рассчитано поле в плоскости Z (рис. 1.6). На рис. 1.6,0 показаны линии равного потенциала несимметричного полоскового вм1новода с учетом толщины токонесущей полоски.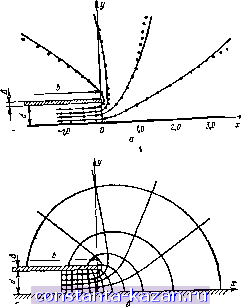

Рнс. 1.6. Линии равного потенциала (а) н картина распределения Поля (б) в несимметричном полосковом волноводе.