щего полиэфира можно получить любую ск-псиь эластичности материала. Пенопласт обладает хорошими электрическими свойствами.

Стеклопласты получают из синтетических полимеров и наполнителей (стекловолокна, полотна и т. д.). Связывающими являются полимеры линейного строения, способные образовывать трехмерную структуру. Стеклопласты разделяют на стеклотекстолиты, анизотропные стеклопласты и стекловолокниты. Свойства материалов на основе стеклопластов приведены в табл. 10.4.

Сополимеры получают сополимеризацией этилена и пропилена, метилметакрилата со стиролом и т. д. в зависимости от области применения.

Сополимеры обладают высокими механическими и электрическими свойствами, стойкостью против химических сред, тепло- и морозостойкостью.

В настоящее время промышленостью освоены пластмассы с наполнением титановыми соединениями. Их основное достоинство - возможность варьировать в широких пределах величиной диэлектрической постоянной, сохранив остальные параметры пластмассы (табл. 10.5).

§ 10.4. Оценка допусков на изготовление полосковых волноводов

Система или узел изготавливаются с определенными допусками как на геометрические размеры, так и на параметры сред и материалов, образующих структуру полоскового волновода. Наиболее существенные среди них допуски на: щирину полоскового проводника 66, толщину диэлектрического листа Ы, однородность диэлектрической проницаемости листа 6е, толщину полоскового проводника 6Д.

Влияние этих отклонений сказывается прежде всего на потерях в линиях передачи. С ростом допустимых отклонений параметров следует ожидать увеличения резистйвных потерь и потерь на отражение. Как известно из теории линий передач, для минимизации резистйвных потерь, т. е. потерь в металле проводников, необходимо изготавливать проводящие поверхности по такому классу точности, чтобы высота мнкронеровностей (а значит, и допуск на их изготовление) не превышала половины глубины проникновення поля в металл. Это ограничение задает требования к точности изготовления 250

поверхностей диэлектрического листа и медной фольги, однако ничего не говорит об остальных отклонениях параметров. Другие допуски, а также и допуск ftil включающий в себя допуски на качество диэлектриче скОго листа и металлической поверхности, влияют на потери вследствие отражений.

Учитывая малость относительных отклонений 6blb, tdjd и др., в первом приближении можно считать, что уровень реактивностей, вносимых микронеровностями, пренебрежимо мал по сравнению с отражениями из-за скачка ролнового сопротивления. Это утверждение тем справедливее, чем меньше геометрические размеры поперечного сечения полоскового волновода по сравнению с длиной волны. При анализе считаем, что два соседних поперечных сечения имеют характеристические сопротивления Z и где 62 - приращение характеристического сопротивления волновода, определяемое суммой приращений от максимальных отклонений всех параметров. Величина bZ может быть охарактеризована полным дифференциалом функции Z=f{b, d, Д, г) и определяется выражением

dZ ... 6Z

(10.1)

где dZ/db, dZ/dd, dZ/дА, dZfde - частные производные по соответствующим аргументам.

Если 62-с2, то КСВН определяется отношением {Z+\6Z\)/Z, а коэффициент отражения

Г| а„с=б2Д. (10.2)

Таким образом, для определения отражений из-за неточности изготовления полоскового волновода необходимо исследовать полный дифференциал характеристических сопротивлений (10.1). При анализе используем формулы (1.98), (1.99) для симметричного и несимметричного полосковых волноводов с воздушным заполнением без учета влияния толщины токонесущей полоски. Тогда в выражении (10.1) два последних слагаемых в правой части исчезают и выражение упрощается. Характеристическое сопротивление в этом случае может быть выражено обобщенной формулой

Z=Al{l + bld), (10.3)

где А = 200 для симметричного и Л = 300 для несимметричного волноводов.

Полный дифференциал выражения (10.3) имеет вид

Максимально возможный коэффициент отражения Г|макг представим тогда следующим образом:

-b + d

fid 86\ [d b)

(10.5)

Анализ выражения (10.5) показывает, что величина отражений определяется идентично для обоих видов вал-

Рис. 10.1, Зависимость коэффициента технологических допусков от размеров полосковых волноводов.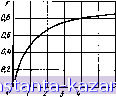

S bid

поводов, поскольку численный коэффициент А в нем отсутствует.

Обозначив F=(j-можем записать выра жение (10.5) в виде

(10.6)

где F=(bld)l(\ + bld).

Очевидно, величина F есть коэффициент, стоящий при линейной разности относительных отклонений Mid и 66/6, определяемых технологическими возможностями. Зависимость коэффициента F от геометрии волновода представлена на рис. 10.1. Б выражении (10.5) в круглых скобках стоит разность допустимых отклонений ddld и 66/6. Поэтому при изготовлении полоскового волновода желательно эти отклонения иметь с противоположными знаками.

Влияние величины диэлектрической проницаемости на допуск волнового сопротивления симметричного волновода исследуем по выражению (1.106). Пренебрегая 252

по-прежиему слагаемым полного дифференциала, 3:iihi-сящим от толщины токонесущей полоски, запищем мл-ксимально возможный коэффициент отражения следующим образом:

rMaKc = 6Z/Z=F,(erf/rf-66/6) -bQ6E/E. (10.7) После несложных преобразований получим

F,= {bld)l{\ + bld), Q = -V2.

(10-8) (10.9)

График Fi=/(6/rf) аналогичен функции F(bld) и изображен на рис. 10.1. Учтем отражения, возникающие за счет изменения толщины токонесущей полоски в сим'-метричном волноводе с диэлектрическим заполнением. Максимальный коэффициент отражения при учете всех факторов запищется следующим образом:

Г|-..с = М?f-Л +Q. -L

(10.10)

Дифференцируя и выделяя отдельные коэффициенты при частных приращениях, получаем

IP, f

Ь ib b + d b

1 8e Д 8д

2 e d - i. A

(10.11)

Из сравнения (10.10) и (10.11) имеем

w f bld + A/d \ f 1 у

F2{bld)l(\ + bld)-

Q.=--\r: L = AI{d-b).

Анализируя полученные выражения, легко заметить, что функция F2 полностью совпадает с F, изображенной на рис. 10.1. Выражение же М переходит в F при устремлении Md->-0. При обычных соотнощениях Д<

<d вместо функции М можно использовать функцию F, и первые два слагаемые примут вид выражения (10.5). В случае сравнимых величин And следует пользоваться последними четырьмя формулами. Влияние отклонений

Рнс. 10.2. Влияние толщины токонесущей полоски волновода на коэффициент отражения.

толщины токонесущей полоски на входной коэффициент отражения учитывается слагаемым /.(бД/Л). Функция L(A) изображена на рис. 10.2.

Полученные выражения позволяют рассчитать отражения, возникающие в линии передачи при заданных . технологических допусках. Они также позволяют установить допуски при известных геометрической структуре и максимально допустимом коэффициенте отражения.

Приложение 1.

ПРИМЕНЕНИЕ КОНФОРМНЫХ ПРЕОБРАЗОВАНИЙ К РАСЧЕТУ ПОЛЕЙ ПОЛОСКОВЫХ ВОЛНОВОДОВ

1. Геометрический смысл функции комплексной переменной. Понятие об отображении

Комплексная переменная zx+]y может быть представлена точкой иа плоскости, причем вещественная часть х откладывается -по осн абсцисс, а мнимая у - по осн ординат.

Естесгвенно, что для изображения комплексной переменной ш= =f{z)=u+]v также можно воспользоваться плоскостью комплексной переменной, но только теперь по осн абсцисс мы будем откладытать вещественную часть и функции f(z), а по оси ординат - мнимую часть V.

Таким образом, мы имеем две плоскости комплексных переменных: плоскость незашисимоп переменной Z и плоскость функции

Каждой точке Zo .плоскости Z отвечает ка.кая-то точка ЕИс плоскости V. Эту точку шо можно назвать отображением точки го на плоскость W (рис. l,fl, б).

При перемещекнн точки г по какой-либо кривой ( в плоскости Z мы будем -получать и плоскости W какую-то крииую L, каждая точка которой есть отображение соответственной точки кривой /, полученное из формулы w=J{z) (рнс. 1,8, г).

Итак, функция комплексной переменной устаиавливает соответствие между точками плоскости независимой переменной Z и точка-пи плоскости переменной V, определяет закон отображения точек одной плоскости на другую.

Если функция w=f{z) однозначна и непрерытня в некоторой области, то любой замкнутый контур, выбряинцй в этой области, отображается также в замкнутый контур.

Действителыю, если будем нз какой-либо точки го обходить контур, то соответствующая точка плоскости W будет двигаться по соответствующей кривой, причем вследствие непрерывности функции a)=f(z) разрыва у кривой быть не может, а вследстяие однозначности, когда г снова придет в го, отображающая точка пр.идет в исходную точку шо. ~

Каждый замкнутый контур С делит пло::кость комплехсной переменной иа две части - внутреннюю и внешнюю (остающуюся при

- , nJi.W

У плг

S mz kv

п - ~б

Рис. 1. Отображение точки н линии