обходе против часовой стрелки - слева и остающуюся ири обходе контура .против часовой стрелки - справа).

Каждой точке области D, находящейся внутри контура С, будет соответствовать какая-то точка плоскости Она будет находиться либо вне. либо Бпутрн контура С-отображения замкнутого контура С.

Но если уж одна точка области D имеет изображение, например, вне С, то и все точки D отображаются во внешнюю часть.

Действительно, пусть внутри D если точка м, преобразующаяся в точку л' внешней части С', и точка Mi, преобразующаяся во внутреннюю точку Mi. Соединим м и Mi непрерывной кривой, не пересекающей С. Этой кривой на плоскости W будет соответстяоиать криваи jkjki, вследствие иепрерыиности пересекающая

/глг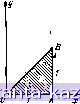

17ЛУ/

Рис. 2. Преобразование треугольника функцией f(z) = \+z.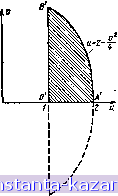

С. Но точке р' пересечении mmi с С на плоскости Z соответствует какая-то точка контура С. Поэтому линия мщ пересекает С, что противоречит условию.

Итак, щш преобразовании с помощью однозначной и непрерывной функции виутрСТпгае (внешние) точк преобразуютси либо нее во внутренние, либо все во внешние точки.

Заметим при этом, что положение точек по отношению к направлению обхода должно быть одинаковым как в плоскости Z, так и и плоскости ТГ. Если, например, мы преобразуем область, находящуюся при обходе С слева, то ей соответствует область, находящаяся слева при обходе С.

Пример I. В плоскости Z задан треугольник, ограниченный линиями х=!1-, у=х; у=0 (рис. 2).

Определить, в какую фигуру преобразуетси этот треугольник функцией ю=1--г*.

Имеем w=u+]v==4+3:=,\ + {x+\y)l+ii+]2xy. Вещественная часть и = \+х^-у^, мнимая часть v-2xy. Если =0, то u=-\ + )fl; v=0. Итак, линия у=0 (вещеспвеняая ось плоскости Z) преобразуется в линию и^О (вещественную ось плоскости W). Если jc=l, то н = 2-ti=2{/ или u=vl4.

Итак, прямой х=1 плоскости 2 соответстиует парабола и~2- -vJi плоскости W. Наконец, если у=х, то н=1; 0=2.*. Поэтому прямой {/-=х соответствует прямая и=1. Вместе с тем точке О (0; I)) сроучетствует точка О'(1; 0) (так как для нее ш-1+0=1), точка А СК 0) преобразуетси в точку А' (2, 0), точка ВЦ, 1) преобразуется в точку В' (1, 2) (так как для нее m = l-l-(l+j)=l4-j2).

Рнс 3. Пример преобразования прямоугольника функцией f(z)=e:

Таким образом, треугольник 0.4В преобразуется в криволинейный треугольник О'А'В' (рис. 2).

Пример 2. В качестве второго примера рассмотрим, в какую фигуру преобразует функция ш=е^ прямоугольник (х=0; Jc=2; у=0; у=\).

В полярных координатах можно записать м ре*® = е^ = е'= eei или р = е*; Q - y. Поэтому линия х = О преобразуетси е окружность р=1, линия х=2 преобразуетси в окружность р-е^ линия у=0 преобразуется в луч 6=0, линия у={ - в луч 0= I (рис. 3).

Найдем теперь линию, а которую преобразует функция w = = к{г + 1/z) окружность \г\ = Я. Положив г = re*, имеем

т = к reJ* -1- е- = и -f-Jo. Выпишем вещественную н мнимую части:

u = k(raisif+ у cosf = AJr+ oosip;

а = sin ¥ - sin = А г- sin у (параметрические уравнения эллипса). Эллипс

В случае г=1 (единичной окружности) эти уравнении дают =2Асо5ф и 0=0, т. е. эллипс вырождается в отрезок (-2fe, +2.к) вещественной осн.

Таким образом, преобразование w = k(z+]/z) перевод|тт окружность радиуса R 9 эллипс с полуосями k{R + \IR) и k\R~\IR). Определим теперь из заданного соотношения ш=(г-н1/г)Аобратную функцию гш=й(2*+1);

- w~

Очевидно, что эта обратная функция совершает и обратное преобразование-нереводят эллипс с полуосями k{R+4IR) и k(R-IR) плоскости W ъ окружность радиуса R плоскости Z.

Если мы хотим преобразовать в окружность эллипс с полуосями с и fr, то надо положить

a=k(R+\IR)\ bk{R-\IR).

Таким образом, kRa + bl2; klR={a-b)l2. Следовательно, е = = (а -* )/4; R={a+b)na-b).

Так преобразование ш =

г-Ь Vz -(д' -И

переводит эллипс

xla+yW=l в окружность u+v{a+b)l(a~b).

Пример 3. Дан эллипс х'1а?+у'1Ь^=Х. Преобразуем его и окружность.

Положим a=k(R+4IR); b=k{R-llR). Тогда a+b=2kR; a~b=. =2klR. Перемножим и разделим последние выражения: с2=о2-62=да. (a+b)l\a-b)R;

W - {г-\- vz - с^ус Эта функции переводит заданный эллипс в окружность и -tflr.

2. Основные виды преобразований с помощью функций комплексной переменной

oj ланел10е ррескразовтил. Линейным преобразованием называется преобразован.ие вида w=Az+B (ш - лииейнаи функция от г), где А В - какие-топостоянные (комплексные числа).

Пусть a=r. Тогда все выписанное линейное преобразование можно разбить на ряд болев простых.

1) г, = ге . При этом преобразовании модуль (т. е. расстояние от любой точки до начала) остается без изменения. Вместе с тем каждый ра.диус-вектор поворачивается на один н тот же постоянный угол а. Поэтому геометрически преобразование Zi=2e состоит в том, что заданная в плоскости z фигура оказывается в плоскости Zi повернутой на угол а без всикого иного изменении фигуры. Такое преобразование называется поворотом (рис. 4,о).

2) z-rzi (Д -положительно). Геометрически это преобразова-нне означает, что каждый радиус-вектор без всякого изменения направления увеличивается в r раз.

Еслн исходная (заданная в плоскости Zi) фигура была прямолинейной, то получившаяся в плоскости Zj фигура будет вследствие

постоянства углов и пропорциона.льности сторон подобна зячашшг Поэтому преобразовапие zrz носит название преобразов.иши подобия (рнс. 4,6).

3) Zz=Z2+B. Это преобразованне есть кэвестное из янадити теской геометрии преобразование параллельного переноса (рис. 4п) Таким образом, всякое линейное -преобразование распадаетсяиа .три элементарных: поворот преобразование подобии, параллельный

Рис. 4. Линейное преобразование.

Пример. Полуокружность г|=1; Гт(г)>0 (рис.-М) преобразуем в полуокружность \w-\2 =2; Ке(ш)-<0. Прежде всего повернем заданную полуокружность на угол Jt/2 (поворот полож1ггель-ный).

Дпя этого надо-сделать преобразование 2, = е^ °2=]г(ри-.5,). Теперь увеличим вдвое радиус окружности гг=2г, (рис. 5,8). Наконец, сдвинем полученную полуокружность вверх на две единицы вдоль мнимой оси (т. е. на 2j) z3=2s-f2j (рис. 5,г). Итак, да=гз = -2j-f2(j2) = 2j(z-fl). Проверяем: точку а= -1 подставляем в ш= =2j(z-f.l), получаем ноль, т. е. начало координат ш.

б) Дробио-линейиое преобразование. Дробно-линейным называется преобразование, выражающееся в виде частного двух линейных функций:

w=(az+b)f{cz+d). (ТТ1.1)

Причем надо считать ad-ЬсфО, так как и противном случае дробь, стоящая в формуле (П1.1), будет сократимой н равна просто постоянному числу. Если в формуле (П).!) с=0, то преобразование будет линейным, а, Ь, с и d могут быть величинами комплексными.

Выделив целую часть, поделим числитель ца знаменатель и запишем функцию ш(г) в виде

р а , b - ad/c а , b/c - ad/c

= ?+7- r + i+d--F+ z + d/c

где а, р и -у - константы:

а=а/с; p=btc-adlc; y=d/c.

Преобразование uj=a+p/(z+v) можно разбить на несколько элементарных:

1) г,=г-4-у -преобразование параллельного переноса.

2) zj-l/zi -обратное преобразование, новое, поха не изученное нами.

3) 2s=pz2 -может быть преобразованием поворота и подо&ид, так как р - комплексная величина (а и -тоже могуг быть комплексными).

4) w=Zt=Z3 + a - преобразование параллельного переноса.

Очевидно, что 1) и 4) совершают параллельный перенос кривых (в том числе и окружностей), не только не меняя их формы, но даже не изменяя их размеров.

Рис. 5. Пример линейного* преобразования полуокружности в плоскости Z.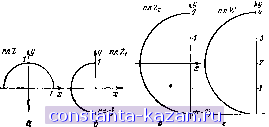

Таким образом, для изучения дробно-линейного преобразования нам надо изучить только преобразования иида ш=1/г.

Запишем его в показательной форме. Положим аг=ре, г =

= ге*, тогда ре* =

i-e-h.

откуда р'= 1/г. 9 = - у.

Таким образом, при указанном преобразоианни модуль заменяется на обратно пропорциональную величину, а аргумент ;меняет знак.

Отметим ттри этом, что каждой точке плоскости Z отвечает одна и только одна точка плоскости W, а каждой точке плоскости W отвечает одна и только одна точка плоскости Z. Однако нэ этого общего закона есть исключение.

Так как деление иа ноль невозможно, то точке г=0 плоскости Z нет соответстиующеЙ точки иа плоскости W. Точно так же на плоскости Z нет точки, соответствующей точке w-Q плоскости W, Если мы буд&м ш акому-либо закону приближать z к нулю, то соответ* ственная точка плоскости W будет удаляться все дальше от начала. Причем направление, по которому булет удаляться точка w, определяется на1Правлением, по которому г стремится к нулю. Подчеркнем еще раз, что каждой точие плоскости кроме z=0, отвечает одна н только одна точка плоскости W, тем более далекая от начала, чем ближе z и нулю.

Чтобы избежать и формулировках ряда теорем дополнительных оговорок, будем считать, что и при z=0 иа плоскости W получаем точку, бесконечно удаленную. Таким образом, согласно нашей термм-нологни, на плоскости комплексной переменной W (конечно, также н на плоскости Z, так как Z=(l/W7) имеется одна условно введенная

нами точка - бесконечно удаленная точка .плоскости. То. что мы ка ллошости представляем себе только одну бесконечно удаленную точку, становится понятным, если плоскость комплексной переменной представить как сферу бесконечно большого радиуса. Бесконеч1НО удаленной точкой будет тогда точка, диаметрально противоположная точке г=0. Отметим уже знакомый нам из аналитической геометрии факт, что Прямую можно рассматривать как окружность б€сконеч;ш большого радиуса.

Вернемся теперь к изучению преобразования ui = l/z.

Z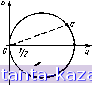

Рис. 6. Дробно-лниейное преобразоиание с помощью функции f(2)-= l/z.

Пример. На шнкжости W найти линию, являющуюся изображением прямой х=1, если ш = 1/г. Так как x=(z-fz)/2, то уравнение заданной линии можно записать в виде z-f-z = 2. Но z=\jw\ z-l/w, поэтому имеем .\lw+\lw=2: w + w=2ww. Так как w=u+iv, то 2н = 2(иЧ-ч^); u-u+v=0; [u-\l2)+v = l/i.

Это уравнение окружности с радиусом г=Л12 и центром в точке (1/2, 0) (рис. 6).

Рассмотрим теперь более общий случай.

Покажем, что преобразоиание ш=1/2 переводит любую окруж-ность в окружность (напоминаем, что прямую мы также считаем окружностью, но только с бесконечно большим радиусом). Уравнение окружности можно написать ш виде а^к^+у')+2bx+2cy+d=0 (а=0 в случае прямой линии). После подстановки г=х-г\у получим

1+Ь (г-f Г)-f J (г-Т)-1-d = О,

откуда с учетом ш = 1/г можно записать

WW \ wJ \ w/

Приводим подобные члены

с

и заменяем wu+jv. В результате d{u+v)+2bu2cv+a=0, что й следовало показать.

Таи как дробно-линейное преобразование, помимо преобразова-нля w = \lz, состоит еще из преобразований подобия, поворота и параллельного'переноса, то можно записать теорему:

Всякое дробно-линейное преобразование переводит окружность в окружность.