Справедливо и обратное заключение

Всегда можно две любые заданные окружности (в частности прямые) преобразовать друг в друга с помощью дробно-линейного преобразования.

Дейсгвительио, нэ геометрии известно, что всякая окружность ПОЛНОСТЬЮ определяется тремя точками. Поэтому нам надо показать, что всегда можно найти дробно-линейную функцию, -переиодящую три произвольно заданные точки zu Z3 -плоскости Z в три ттроизвачьно заданные точки Шь Шг. и^з плоскости W.

Запишем дробно-линейное лреобразование ввидеш = а+р/(г+). Это выражение содержит три произвольные -постоянные (комплекс-иые) а. р и -у. Для определении их надо иметь три уравнения. Получаем нх из условии соответствии трек точек:

Однако такой дштод отыскания вида дробно-линейного преобразовании требует довольно громоздких вычнслеинй. (Эти уравнения не первой степени,- решить их трудно.) Поэтому да,дим более простой метод вывода формулы нужного преобразования.

Помимо плоскостей Z к W, la каждой з которых нам заданы и точки, возьмем вспомогательную плоскость . Найдем функцию (г), переводящую 1х>чку zt плоскости Z в точку О плоскости Очевидно, такой функцией является =z-zi (действительно, при г=г, Ci=0).

Теперь составим функцию w, переводяшую точку i=0 плоскости в точку w-Wi плоскости W. Очевидно, w--\-Wi или = = w-Wi. Так как % одно и то же в первом и втором случае, то, приравнивая пх, получаем овязь между плоскостью Z и плоскостью W:

W-Wi=Z-Zi.

Это преобразование переводит точку z=Zi плоскости Z в точку Wi плоскости W.

Будем телерь подбирать функцию ?(г), по-прежнему переводящею г=г1 и ?1=0. так чтобы она переводила также точку г=2г

Наша прежняя функция ?=г-г, при г=г2 обращается в гг-гь Следовательно, чтобы она обращалась при z=Z2 в единицу, надо выбрать ?-(2-0i)/(Z2-ziT Теперь найдем функцию Wi, .переводящую точку £=0 в w=Wi, а также точку =1-в ш = Ш2. Таковой будет, конечно, функция, определяемая нз равенства

5=(Ш-Ш1)/(Ш2-Ш]).

Действительно, прн ?=0 ш=ш, и при =1 ш=шг. Соотношение между плоскостью Z и плоскостью W:

Z - Zi W- Ш|

Z2 - Zi Wz- Wi

Наконец, подберем функцию переводящую z=Zi ш t,L=0, г=г2

в Ь=1 и z=Z3 в 5а оо,

Рассмотрим функцию

Zj - г, Z - Z,

При z-Zi она обращается в ноль, при г=гз - в бесконечность. Наконец, при z-zj она обращается в il/(Z2-гз). Чтобы искомая функция обращалась при z=Z2 в единицу, надо выписанное выражение умножить на Za-Za.

Итак, функция К= - % переводит 2 = г, в S, = 0, z=

= Zg в ?г - 1, г = Z, и = OD.

Как и ранее, стронм функцию ш, переводящую точку ?=0 в ш - -ail, точку Е=1 в ч> = Ш2, точку Е=оо в w=w,. Эта функция определяется равенством

а? - ш, Ш2 - 1

Wz - Wi W - Шэ

Таким образом, имеем

zi; - w, ш - г

г-Zi z; -г. Zj - г, Z - Z,

(П1.2)

Функция Mj(z), определяемая этим равенством, есть, очевидно, дробно-линейная функция от Z. Вместе с тем ясно, что при z=Zi w=wu при z=zj ш = Ш2 и прн z=z3 ш = а)з. Если одно яз чисел zi, или ш обращается и оо, то и в числителе, и в знаменателе (Л1.2) разности, в которых участвует это число, надо заменить единицей.

В качестве примера получим формулу, дающую преобразование единичной окружности в вещественную ось. Выберем на единичной окружности (окружности радиуса 1) трн точки: Zi=.; Z2=-I; z, = j. На вещестиенной оси выберем точки Ш1=0; Шг-=сю; ffls=.l. Подставляем значенгя гь и Шв в формулу (Ш.2) получим

Ш Ш; - I Z - 1 -1-]

Wt ш - I -2 г -j

tf mg - 1 z - 1 I - j w - 1 Шв - 2 z - j

Так как (wj-)/ш2=1, можно записать

ш/(да-l) = (z !i - 1 z -1

-I)(l+))/2(z-/);

z-1 1-1-J

l (z-)(l-j)

Ш z - 1

-u -=i-

(-i)(i-i).

z- 1

Окончательно ш=] (1-z)/(l+z).

Отметим, что это преобразование не яиляется единственным дробно-лннейным преобразоианяем, переиодящим единичную окружность в вещественную ось.

в) Преобразование посредством показательной функции ш=е^. Так как z=x+]y. то ш=е*+*=е* е' ю представляем и виде t =pe откуда р=е*; 9=.

Таким образом, линиям x=const плоскости Z соответствуют линии p=const, т. е. окружности с центром в начале координат плоскости W. Линиям =const плоскости Z соответствуют лучи 0-const плоскости W.

Полосе Qlm{z)n плоскосггн Z отвечает вся верхняя полуплоскость плоскости W.

Если же взять несколько полос шириной 2л, -получим несколько плоскостей W, наложенных одна на другую. Таким образом, нреоб-разованне, с. помотью показат^1ьнпй функции не явлйется7 как и следовало ожидать, взаимно однозначным вследствие многоэнач-ности лоари^а.- --

~ ункцня, обратная функции ш=e т. е. г=1п ш (многозначная функция), переводит, очевидно, сетку полярных координат в сетку декартовых координат. Преобразование с помощью показательной функции переводит сетку прямоугольных декартовых координат в сетку полярных координат.

г) Преобразование с помощью степепной функции а)=.г , это преобразование применяется обычно в случае, когда произвольный угол плоскости Z надо преобразовать в полуплоскость плоскости W.

Пусть в плоскостн Z задан угол а с вершиной в начале координат и стороной, нвправленной по вещественной оси (О агц г =С а). Положим ш^г и ш-ре(г = г'*е^ 0. Тогда где

= arg2L Сторона 1ф=0 заданного утла перейдет в луч 6=0, а сторона ф=а - и луч в=па. Таким образом, видим, что аргумент возрос в п раз. Если мы хотим преобразовать заданный угол в верхнюю полуплоскость, то надо положить па=л. Тогда =я/а.

Итак, преобразование w = z переведет заданный угол в верхнюю полуплоскость. Если вершина угла расположена не в начале координат, то надо сначала перенести вершину в начало:

Zi=Z-Zt.

Если заданный угол не имеет стороны, совпадающей с вещественной осью и его стороны образуют с осью соответственно углы р и а+Р, то предиарительно надо повернуть угол на величину -р, т. е. сделать предварительное преобразование

Итак, в общем виде наше преобразование можно записать следующим образом;

4 = ш = [(г - г.) е-Щ' = (г - г.) е ? .

Это преобразование переводят, как указано выше, угол а плоскости Z в верхнюю полуплоскость плоскости W. Отметим, что геометрическая картина преобразования сохранится при применении дополнительного любого преобразования подобия, т. е. при выборе функции

Пример 1. Угол (область) - st/4 eg arg (г - jX st4 преобразовать в верхнюю полуплоскость (рис. 7,0). Переносим вершину в нача.чо координат: 2, = г -j (рис. 7, б). Поворачиваем область на угол п/4: Z2 = e*Zj (рис. 7, в). Так как о = п/2. то rt = 2 и функция преобразования будет яметь вид

w=4 = Hz-i) е *] = (г - J)= el = = ] (г - j)=.

Окончательный результат представлен на рис. 7,г.

Пример 2. Угол 0>arg(2-!)>-я/6 преобразовать в верхнюю полуплоскость (рнс. 8). Прежде всего надо угол перенести в начало координат. Код-да z=l, Zi должно быть равно нулю. Следовательно,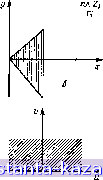

Рис. 7. Преобразоиание с помощью степенной функции.

21=2-1. Дальше переводим угол виерх (над вещественной осью). Надо повернуть угол на п/6, следовательно, необходимо изменить аргумент, т. е. увеличить его на л/6. Для этого умножим аргумент на е

2, = 2,е1 /5.

Дальше надо получить верхнюю полуплоскость. Соотношение будет ш=2*. Окончательно получаем

W = 2 = ((2 -1) е'/ ] = (2 - !) е' = - (2 - 1).

Это преобразование переводит угол л/6, лежащий ниже оси х плоскости г, в верхнюю полуплоскость плоскости W. 18-732 265

Рис. 8. Пример преобразования части плоскости Z функцией /(г) =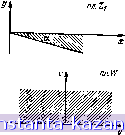

3. Геометрический смысл производной от регулярной функции

Как и в теории вещественной переменной, целесообразно выяснить геометрический смысл понятия производная .

Пусть в плоскости Z задана точка zu\ в плоскости W ей соответствует точка Шо, определяемая соотношением шо= (2о). Проведем через точку произвольную кривую /. В плоскости W ей будет соответствовать какая-то кривая L, проходящая через Шо. Выберем на I произвольную точку г и рассмотрим комплексное число (вектор) Az=z-zo.

Соотщегственно на плоскости W имеем точку w и отрезок Как известно из курса математики, производная

Поэтому для определения производной надо изучить поведение комплексной величины t=Aw/tiz при Az-уО.

I Да)

Имеем ]t\ = -

и arg ( = агЕ Дш - arg Дг. Поэтому arg t

есть угол, на который повернулся вектор Дг irpn его преобразовании ва плоскость W.

Еслн Дг->-0, то аргумент вектора Дг стремится к углу, образованному касательной к / в точке Zo с вещественной осью. Точно так же аргумент стремится к углу, образованному касательной к i в Шо с осью и. Поэтому аргумент t стремится к разности между углом, образованным касательной к L в Шо, и углом, образованным касательной к ( в zkj. Но если функция регулярна, то производная динственна и не зависит от способа стремления Дг к нулю, т. е. от выбора кривой (, а потому не зависит от выбора / и аргумент

этойпрйизводиой. HiaK, argf (zo) есть угол.ггоиорота касательной к любой кривой, проведенной через точку .Zj прн ее преобразовании иа плоскость W. Модуль F{zt) показывает, во сколько раз Дг меньше соответствующего Дш, т. е. во сколько раз увеличивается длина бесконечно малого элемента плоскости Z при преобразовании на-плоскость W с помощью функц-ии w=F{z). Модуль производной f(ai) характеризует изменение линейных раэмеровв точке zo прн преобразовании, совершаемом фуЕжцией F{zt).

Еслн, например, F(z)=z+z+3, то при преобразовании лпней-ные размеры в точке z=il увеличиваются в трн раза: /(г)1 = = 2г-Ц = 3.

4. Формула Кристоффеля - Шварца

Пусть теперь требуется преобразовать на верхнюю полуплоскость йногоугольннк. Ради простоты будем решать обратную задачу: преобразовывать верхнюю полуплоскость на заданный многоугольник.

(Многоугольник этот может иметь одну нэ вершин в бесконечности, т. е. быть фактически не замкнутым.

а

2; X

Рис. 9. К выводу формулы Кристоффеля-Шварца.

Обозначлш через wi, Шг, ..., ш„ вершины многоугольника. Через not, лая, ..., пап - его внутренние углы, а через Zi, zi, .... z - точки вещественной оси, преобразуемые в вершины многоугольника (рнс. 9).

Положим, наконец, что сторона ш„ш, многоугольника лежит на вещественной оси плоскости W (рис. 9,6).

Как показано ранее, угол поворота касательной к заданной кривой прн ее преобразовании иа плоскость W есть аргумент производной. Значит, при г. выбранном между z и Zi, аргумент производной равен нулю; т. е.

dw

arg- = 0.

Если же zi<z<Z!, то отрезок z,zz переидет в отрезои wiwt. касательная направлена под углом л-яа1-я(1-lOi) =1171. Следовательно, аргумент производной равен dw

aig- = IU -по, =п(1 -11,) = iry где Yi = l- i-