стям. в Приложении 2 показано, что поток энергии через поперечное сечение реального полоскового волновода соответствует потоку энергии в преобразованной плоскости I.

Учет конечной проводимости токонесущей полоски сводится к введению небольшой тангенциальной составляющей электрического поля.

у

Плоскост Z

PiK. 1.7. Площадь интегрирования для определения мощности, передаваемой вдоль несимметричного полоскового волновода.

Для определения потока энергии через поперечное сечение- реального полоскового волновода в плоскости Z необходимо найти это сечение в плоскости . Для этого Воспользуемся .уравнением (1.7), переписав его в виде

z=~\w-\-\nw-\- 1 -(1d-\У2ld)(w-\-1)1. (1.11)

Подставив в выра.кение (1.11) координаты точки С рис. 1.7), получим

A[w-\-{t\w-\-1 -(2uW-f 1/2Д7Э)(в!)-1- 1)].

(1.12)

Комплексную величину в плоскости W можно представить как произведение модуля на аргумент ш = ге*. Тогда уравнение (1.12) можно переписать иначе:

-I- = ir cos9+ In г 1 - (2u/d + уШд.) X

X (г cos 1+1)];

jd=[г sin j+ -j- - (2A/d + У2Ш)(Г sin jv)].

При <jj = iE будем иметь

-[ r+lnr-t- 1 -(2Ad--/2u(d)(l - r)l

/(/ ) = ; -In/- - 1 - iift/(2d)-(2A/d-f/2A/dj(r-l) = 0.

(1.13)

Значения корней <Га и гв трансцендентного уравнения (1.13), определенные в области изменения аргумента Ii6/djg20, даны в Приложении 2.

Имея значения корней и для данных отношений bjd и Д/d, можно подсчитать площадь S,. поперечного сечения плоского конденсатора в плоскости С и тем самым определить Р^.

Sj = (lnra-lnr). Мощность, проходящая через это сечение.

Подставляя в последнее выражение значение Е^, а также

учитывая, что мощности в плоскости Z и в плоскости ь инвариантны и что при конформном преобразовании в плоскости Z рассматривалась половина поперечного сечения несимметричного полоскового волновода, определим мощность, проходящую через полное поперечное сечение (Вт):

Р, = 8,44- 10-/в71 dnnrjr. (1.14)

Зная мощность Р^, передаваемую по несимметричному полосковому волноводу, и мощность потерь ДИМ затухание (Нп/м) [43]:

3- 2Р,

In. г в/г

-(-21п(г^а/2)-.

2Zpd

In rg/r

(1.15)

Последнюю формулу можно упростить й привести к виду, удобному для инженерных расчетов. В первом приближении, полагая, что

получаем

Агв+1 2 1nr-fl/2

где CR=2/2A/d; Z.= 120ti.

В работе [121] затухание волн в несимметричном полосковом волноводе, заполненном неоднородным ди-

электриком, определялось

методом, основанным на принципе бесконечно малого Приращения индуктивности . Этот метод может быть применен только в том случае, когда можно рассчитать внешнюю индуктивность, т. е. если в полосковом волноводе распространяется волна типа ТЕМ. Метод предполагает, что толщина токонесущих полосок и заземленных пластин заметно больше глубины проникновения тока и углы полосок закруглены. Для тонких токонесущих полосок (3 ... 4 толщины поверхностного слоя) на практике эти условия выполнить невозможно.

При выводе формулы для затухания значение погонной индуктивности принято равным значению для несимметричного полоскового волновода, заполненного однородным диэлектриком.

Несмотря а вышесказанное, метод бесконечно ма- лого приращения индуктивности был применен для нахождения затухания волн в несимметричном полосковом волноводе. Очевидно, это сделано потому, что нахождение точной формулы для определения затухания путем 30

Рис. 1.8. Зависимость затухания от геометрических размеров несимметричного полоскового волновода.

прямого интегрирования уравнений электромагнитного поля представляет трудную аналитическую задачу.

Полученные в [121] три формулы для определения затухания очень громоздки и справедливы каждая в своем интервале отношений bjd. Первая для6/й^0,16, вторая в пределах 0,16<6/d2 н третья 4>6/rf>2. Расхождение между вычисленными значениями затухания по приведенным формулам и измеренными экспериментально не превышает (6...8)% [121].

Полученная формула (1.15) для определения затухания волн в несимметричном полосковом волноводе прямым интегрированием уравнений электромагнитного поля справедлива в широком диапазоне отношений Ш.

На рис. 1.8 приведены кривые зависимости нормированного затухания волн в токонесущей полоске и заземленной пластине от отношения 6/d, рассчитанные по формуле (1.15) для возможных значений Д/d.

Пример. Для отношения bld=2, A/d=0,01, rf=(1.0 мм. f=l ГГц полученное mo данным (.131] затухание Р^О/19 дБ/м. Рассчитанное по формуле

/ ln(r.a/2) 8,26.10-.6,075-8,68

1п(Гд/г^) = 377.10-.5,903 =:° ДБ/ -

Расхождение fi%=3%.

Для отношения 6/d=4, A/d=0,OI, d=l,0 мм, f=l ГГц затухание согласно 1Э1] Р^Д93 дБ/м. По формуле ЦХЛЪ) находим;

8.26.10- 377.10-

9,237.8.68 9,542

= 0,184 дБм.

Расхождение в%=4,65%. Для отношений 6/d>4 в работе (121] данных не имеется.

Приведем еще результаты для отношения b/d=lO, A/d=0,01, d= =11,0 мм, f=l,0 ГГц. Из графиков, приведенных .в fl23], находим Р^.19 дБ/м. По формуле (1.15):

8,26.10- 18,658 Р = -377Л0Т9:688 .68= 0.181 дБ/м.

Расхождение в% = 4,73%.

Для отношений fc/d>2 результаты расчета по формуле (1.15) хорошо согласуются с данными, приведенными в работах [121, 123]. Расхождение результатов (примерно 57о) при определении затухания объясняется тем, что в указанных работах использован приближенный метод бесконечно малого приращения индуктивности , предложенный Уилером [128].

Для отношений b/d<2 формула (1.15) дает погрешность: для ft/d=l б%=20%, для bld<\ 6%>25%.

Для узких токонесущих полосок (6/dl,0) в работе [48] приведена формула для затухания волн в несимметричном полосковом волноводе, которая хорошо согласуется с результатами, полученными Шнейдером [1231

Если учесть шероховатость поверхности меди токонесущей полоски (как это предлагается в работе [125]), то величину поверхностного сопротивления надо увеличить на 13% при частоте /=1 ГГц и на 33%-при /=6 ГГц. Б этом случае результаты расчета по формуле (1.15) близки к экспериментальным.

Формулу (1.15) можно упростить. Для отношений bfd>\ \п(гв1гл) можно заменить гв- Тогда получим простую формулу, справедливую для большого интервала отношений b/d (от 1 до 10): 1?

(1.15а)

§ 1.4. Мощность пробоя и максимально допустимая мощность, передаваемая через поперечное сечение несимметричного полоскового волновода

Для инженерных расчетов можно упростить формулу передаваемой мощности. Для отношений b/dl в формуле (1.14) логарифм отношения Гв и Гл можно заменить Гв- Тогда для несимметричного полоскового волновода с воздушным заполнитеелм формула передаваемой мощности принимает вид:

P, = 8,44.10-£dVfi. (1.16)

Для определения мощности пробоя рассмотрим изменение напряженности электрического поля в поперечном сечении несимметричного полоскового волновода [41]. Напряженность электрического поля в любой точке поперечного сечения полоскового волновода (исключая проводящие полоски) в плоскости Z определяется формулой E = E{Xldz), где черта над комплексной производной указывает на комплексно-сопряженную величину; £j-поле плоского конденсатора в плоскости'С

E, = i-.

Напряженность электрического поля по модулю

\ЕА =

3 -и.

(1.17)

где Е„ - однородное поле в полосковом волноводе; 1

; Л = (1 - l,4l/uW).

Подставляя в формулу (1.17) значение г]=п„ для верхней полоски получим

(1.18)

Подставляя в (1.17) т)=0, для нижней пластины будем иметь:

(1,19)

На рис. 1.9 показаны кривые изменения напряженности электрического поля вдоль верхней полоски и нижней пластины, рассчитанные по формулам (1.18) и (1.19). Из рис. 1.9 видно, что на краю верхней полоски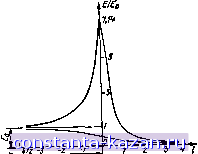

Рис. J.9. Изменение напряженности электрического поля в поперечном сеченни несимметричного полоскового волновода: Д/й=0,01; £ .кс=7.14£>

3-7S2