при 1=0 Е1;111ряжеп1юсть электрического поля имеет максимальное JHiHIlMEHC

макс -£ft

А - 1

==2Eja.

где Ео - напряженность однородного электрического по ля в полосковом волноводе;

Л=1-а/2; a = 1V2EJl + ijd + ...

ПpeдeльнaяJVllOщнocть полосковых волноводов огра- ничивается максимально допустимой величиной напря- женности электрического поля у края токонесущей полоски. Для пробоя промежутка межд> плоскими электродами в воздухе при нор.мальном атмосферном давлении нужна напряженность электрического поля порядка [23]

ЯпрОЗ- 10 в/м.

Следовательно, в нашем случае напряженность поля не должна превышать величины £макс, т. е.

Но=£макс-а/2<£пр 0/2. (1.20)

Тогда, подставляя Е^ в (1.16), получаем формулу для определения мощности пробоя

Р„=8,44.10-£(a=/4)dV = 2,ll. lO-/ff (1.21)

Зная мощность пробоя, легко определить максимально допустимую мощность, которую можно передать через поперечное сечение несимметричного полоскового волновода:

- P ..c = 2.1M0-.£° a.dV (1.22)

где£макс=1,5-10 В/м.

Формулы (1-21) и (1.22) можно еще упростить, приняв a==2V2u/d. Тогда

Рпр' 16,88. W-E d{/d)r; (1.23)

Рм , 16.88.10-£/(Д, )г^.

(1.24)

1Прн6лижен.ная формула пробивной мощности (1 23) была проверена экспериментально. Несимметричный полосковый волновод своз-душным заполнителем имел следующие размеры: ширина токонесущей полоски Ь=4,7 мм, ее толщина Д=к0,12 мм, расстояние между 34

полоской и заземленной пластиной £/=0,94 мм, характеристическое солротнвлецие волновода Z=50 Ом, погонная емкость С=0,636 пФ/м 141].

Пробой полоскового волновода наступал при мощности, в среднем равной 40,6 кВт.

Следует заметить, что лробой начинался на краях токонесущей полоски (рис. 1.9), где напряженность электрического поля имела максимальное значение.

Теоретическая величина мощности пробоя, подсчитанная по формуле (1.23), для отношений fc/d=5 и Vd0,125

/, , . Ui,B8 IU (,Ml) )2. (0,94.10-3)2.0,125-23= = 10,88.9.0,88-0,125-23 10=36,6 кВт.

Как видно из расчетов, теоретические и экспериментальные величины пробивной мощности несимметричного полоскового волновода с воздушным заполнителем хорошо согласуются. Погрешность не превышает 5%.

Максимально допустимая мощность, которую можно передать по несимметричному полоско-Е )му волноводу с воздушным .киюлнигелем, определяется из формулы (1.24). Подставляя значение Я„а„с=1,5-10 В/м, получаем

Рмакс= 16.88Х

ХЮ-(1,5-10 )2Х X(0.94 10-3) 2.0,125 X

Х23=9,67 кВт. Допустимая мощность.

о

б 6/d

Рис. 1.10. Зависимость передаваемой мощности от геометрических размеров несимметричного полоскового волновода

как параметр полоскового волновода имеет большое значение, поскольку

определяет возможности применения полосковых волноводов.

Зависимость максимальной передаваемой мощности от геометрических размеров несимметричного полоско-вого волновода представлена на рис. 1.10. 3* 35

§ 1.5. Расчет поля в симметричном полосковом волноводе с воздушным заполнителем

Основным видом колебания в симметричном полосковом волноводе (рис. J.ll.a), так же как и в несимметричном, является ТЕМ волна. Векторы поля лежат в плоскости поперечного сечения полоскового волновода и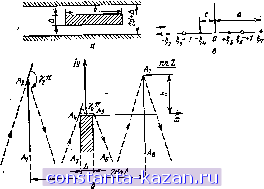

Рис. 1.11. Конформное лреобразоваике симметричного полоскового ролновода:

3 полоскового волновода, где Ь - шнрн-

а - поперечное сечение снмметричнию нилишиви! и i.imiii..i.um . . - - на центральной токонесущей полоски, Д -толщина, d-расстояние между центральной полоской и эвземленнЬМИ плвстннами; б - последовательность преобразования; в-вещественная ось отображения,

само поле является поперечным. Поперечное поле в этом случае удовлетворяет уравнению Лапласа, т. е. оно имеет так-то же структуру, как и в электростатическом случае.

Считая пластины полоскового волновода параллельными друг другу и бесконечно протяженными, приходим к плоскопараллельному полю. В случае плоских полей можно использовать методы конформного отображения.

Как и ранее, будем вычислять электростатическое распределение для одной половины поперечного сечения полоскового волновода при допущении, что другая половина простирается до бесконечности. Электростатическое 36

распределение для второй половины поперечного сечеНиЯ волновода получится из условий симметрии (рис. 1.11,6).

Для определения расчетных формул будем обходить проводящие поверхности полоскового волновода, как показано на рис. 1.11,6, по пунктирным линиям. Точке Ai(Zi) плоскости Z в рассматриваемом отображении соответствует точка -i=-со в плоскости точке 2(22)-точка I-2=а (а требуется определить), точке Ла(2я)-точка ,з=-1, точке i44(2i)-точка -1=0 (с требуется определить), точке Аь(г^)-точка 5=с|, точке Л(1(2б) -точка б=--1, точке 7(27) -точка 7 = 0, точке /1 (гв) - точка Е8=--оо (рис. 1.11,в). Из сообра-

Ж Ч1ПЙ СИММегрЕЕП следует, что bi = 7 и Г|4 = 5.

Точкам 5з и в соответствуют изоляторы.

Будем осуществлять отображение вещественной оси плоскости I, на многоугольник плоскости Z с углами при вершинах, равными ята, пуз, ., лу7, с помощью npepia-разования Кристоффеля - Шварца:

(1.25)

Величины , 5, Ъ, (2<Е4<15<7), соотвстствую-щне различным вершинам многоугольника, подлежат определению.

В нашем случае углы поворота равны:

згу2=-я; Щз=я; Яу4 = -л/2; яу5=-я/2; яуб=л; лу7=-л,

где яуг - внешний угол в соответствующей вершине многоугольника. Отсюда находим уг: у2=-1; №=1; л;4= =-1/2; V5=-l/2; уб=1; У7=-1.

Подставляя значения Vt в (1.25), получаем

dz dt.

(1.26)

Выражение (1.26) записано в предположении, что точки 1и соответствующие вершинам многоугольника, известны. Однако нам задана лишь геометрия многоугольника в плоскости Z, т. е. положение вершин многоугольника Ai и углы Yi (в долях л), а положение точек \i подлежит определению. Таким образом, каковы бы

ни были числа функция (1.26) определяет отображение, которое преобразует многоугольник плоскости Z в вещественную ось плоскости

Прежде чем интегрировать выражение (1.26), произведем подстановку \п=а, с=<\. В результате получим

, = c}-Sl=4rfC. (1.27)

Подынтегральная функция всюду, за исключением точек 7=о; 4=с; з.е=±1 и ±сх), аиалитична и отлична От нуля, отображение г(Х^ вне этих особых точек конформно.

Для рещения интеграла (1.27) воспользуемся подстановкой Эйлера

ух. - c - t~ti, откуда находим Ц;

It 2<=

Подставляя значения £ и в формулу (1.27), после преобразования получим

fо - 4п'( + (8д'с' - 2с') г' - 4а^с'< + с' 28)

f + (2c - 4) < -f сЧ

Под интегралом в (1.28) получена дробь, числителем и знаменателем которой служат полиномы, содержащие только целые степени независимой переменной t Такая дробь называется рациональной, и так как степень числителя выще степени знаменателя, то из данной дроби можно выделить целую часть.

Разделив в указанной дроби числитель на знаменатель и взяв интеграл от целой части, получим

j2,o Г (4 -2с'-4а')< -К8а'е' -Зс)<* -4aV<-fc /+J t{l + 2t + c){t - Zt + c) /

(1.29)

Преобразовав в знаменателе (1.29) сомножители в круглых скобках к виду [(<-f I)-fс^-1] [(-l)-f-+ -1] и сделав замену 1-с' = Ь\ выражение (1.29) можно записать следующим образом:

+ J t(t + l+b){t+\-b)V-l + b)(t-l-b) 38

Подынтегральное выражение (1.30) представляет дробь, знаменатель которой имеет более низкую степень, чем числитель. Такая дробь может быть разложена на сумму элементарных дробей, знаменателями которых будут множители знаменателя дроби подынтегрального выражения (1.30).

Итак, z=4- {m-{-[AJf + AJt + AJt-{-AJ{t-{-

\+b) + AJ(t-{-l -b) + AJ{t -14-6) + AJ(t - 1 - 6)1 dt],

(1.31)

где ,1i ... Ai - [гмсгояипые, которые следует определить.

Гоотпетстпепно тому, что в (1.30) множитель t входит в знаменатель в третьей степени, мы ввели в (1.31) в знаменатель как t, так и все низшие степени множителя t.

Дробь под интегралом в (1.30) тождественно равна сумме элементарных дробей под интегралом в (1.31). Обе дроби представляют собой только различные формы выражения одной и той же функции. Если эти дроби освободить от знаменателей, то обе части получающегося равенства также будут равны тождественно:

(4 2са-а2) (8а2с2-Зс ) t~id?cti+lfi

Л,[(*-Ы) -бг] [{t-\y-b]+A,[{t + \)~

-62] t+As[{t+\r-b] [(t-\)-bt +

+A,Ut+l)-b] Ht~\)-b]t=+A,Ut+\)+b\ W-i)~

-62]<3-ЬЛе[(<-1)-6] [{t+\y-b]t+A-,[(t-l) +

+ b] [(t+l)-b]t. (1.32)

Постоянные A, часто легче определить путем подстановки вместо / частных значений. Уравнение (1.32), как было уже сказано, представляет собой тождество, а потому удовлетворяется при всех значениях t. В частности, если =0, оно принимает вид

4i(l-62)2 = c8,

Полагая таким t=\-b; tl+b,

- =с', так как 1 -Ь' = с'.

же образом t=-1-6; t=-l+b; получим Л2=0; Лз=4-2с2-4о2;