Уравнепнс (1.1)2) позволяет при заданных потенциалах определнгь напряженность ноля по величине и напр авлениго в любой точке верхней полуплоскости 1т^>0 при помощи простого дифференцирования.

Определив из формулы (1.62) производные йф/ и d(fldr\, получим напряженность электрического поля в произвольной точке верхней полуплоскости 5 н следующем виде:

S-1 V-bffi-D

(i:63)

Из точек вещественной оси плоскости t, линии равного потока выходят под прямым углом к ней, и напряженность поля в них определяется по формуле

Напряженность Ez в плоскости Z может быть определена по формуле (П2.1).

Дифференцируя формулу (1.58), получаем

Подставляя последнее выражение в (П2-1), имеем

где черта над выражением в круглых скобках говорит о том, что надо брать величину, ему сопряженную.

Формула (1.64) показывает, что максимальное по.пе будет на краях центральной полоски. Поэтому при конструировании полоскового волновода надо тщательно обрабатывать края центральной полоски, закругляя их.

Для определения поля в плоскости Z задаются величины Д и d, по ним вычисляется q (1.56). Далее задаются точки i, rii плоскости £ и по ним вычисляются точки л; и 4Г в плоскости Z (1.57) или (1.58). Используя выражение (1.64), производится расчет напряженности поля симметричного полоскового волновода без учета толщины центральной полоски. 52

Для расчета напряженности поля симметричного волновода с учетом толщины центральной полоски необходимо использовать выражение

полученное аналогично (1.64) после дифференцирования (1.57) по S.

Формула (1.33) была проверена экспериментально. Моделирование электрического поля симметричных полосковых волноводов с воздушным заполнителем проводилась так же, как и несимметричных на электропроводящей бумаге.

Д.пя построения линий равного потенциала и равного потока формулу (1.33) приведем к параметрическому виду.

-t- (1 -г-(vn 4 in щ^ f/y (I

где

M = {0,511/(P + 4?V + (P ~ f- c)l} ;

W = {0,5(/(S-f-c )+4?Y-(P--c)]} l№-fM)=-(>!-fW)-<i-bb)] 1(1-1-Af)-(ii -f Y~(->n+ (1+

fO, если 6=0; ъ, еслис<?<1, i) = 0; arctg Q, если Q>0; 0, если 5> 1, Yi = 0.

По этим формулам рассчитано поле в плоскости Z. На рис. 1.16,ij показаны линии равного потенциала в поперечном сечении симметричного полоскового волно-

вода с учстм толщины токонесущей полоски, где точками отмечены экспериментальные значения. Опытной проверке подвергались симметричные полосковые волноводы с различными геометрическими размерами. Эксперимент подтвердил правильность аналитических расчетов.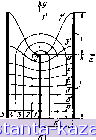

Рис. 1.16. Линии равного потенциала симметричного полоскового волновода (а) и теоретическая картина поля в поперечном сечении симметричного аолновода (б).

Численные значения линий равного потенциала и равного потока, необходимые для построения картины поля двух симметричных полосковых волноводов с параметрами di=l мм; Ai=0,l мм; и Й2=5 мм; Д2-= =0,1 мм; hld2=\, даны в [41] в Приложении 5, табл. 6-11.

На рис. 1.16,6 изображена картина распределения поля, рассчитанная по параметрическим уравнениям.

§ 1.6. Определение передаваемой мощности, потерь и затухания в симметричном волноводе

Формула (1.65) позволяет определить напряженность электрического поля в любой точке симметричного полоскового волновода, если известна напряженность поля в плоскости Воспользуемся этой формулой для нахождения потока энергии вдоль полоскового волновода.

Мощность, передаваемая вдоль полоскового волновода, определяется средним по времени значением интеграла от продольной составляющей вектора Пойнтинга 54

по площади поперечного сечеНия:

/>, = JES = 4-[£W*],dS. (1.10а)

Зная связь между напряженностями электрического и магнитного полей, последнее выражение можно записать в следующем виде:

Pz=\V4Fv.\E,YlS, (1.106)

где dS-элемент площади поперечного сечения симметричного полоскового волновода.

Использовав соотнощеиие (П2.2) в формуле (1.106), вычислим мощность в плоскости

(1.66)

где dt,- элемент площади в плоскости 5.

Следовательно, найдя мощность в плоскости определим мощность в плоскости Z, так как Рг = Р^-

Площадь поперечного сечения полоскового волновода в плоскости £ нам не известна. Переходим к ее определению.

Мощность вдоль симметричного полоскового волновода проходит через поперечное сечение ABiEiFA и СВгЕЖ (рис. 1.17).

Функция (1.57) отображает поле симметричного полоскового волновода в верхнюю полуплоскость плоскости £ (ImS>0) и для точки г=Л/2-j6/2 (рис. 1.17) имеет значение

A2-j6/2=j4(-Alnb.+ ,n4). (1.67)

После преобразования последнего выражения получаем уравнение, позволяющее определить соответствие границ реального полоскового волновода в плоскости Z границам на оси :

ж

q(\-cf) °=Е;(1 5=). (1.68)

Здесь - корни уравнения (1.67), определяющие границу проводяи;их поверхностей полоскового волновода в плоскости ,

с=ДМ- a=bld. - (1.69)

Уравнение (1.68) может быть решено численными методами, однако, исходя из физических представлений в пределах геометрии полоскового волновода, используемой на практике, решение можно упростить, разделив

уравнение на две части: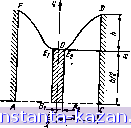

(1.70а)

E. = Vl-e- \

(1.706)

где 5,-с - корни уравнения, определяющие границу проводящих поверхностей между центральными полосками; .-а - корни уравнения, определяющие границу проводящих поверхиостеи снаружи центральных полосок.

Такой переход возможен в предположении отсутствия существенного взаимодействия поля на внутренних и внешних поверхностях эквипотенциальных полосок. Произведя преобразование поля в плоскости t, в поле идеального конденсатора в плоскости с расстоянием л между обкладками (см. § 6 Приложения 1), получим преобразующую функцию в виде

Рис. 1.17. Площадь интегрирования для онредсления мощности передаваемой вдоль симметричного полоскового волновода

. = 1п-.

(1.71)

откуда положение граничных точек щ и иг идеального конденсатора с учетом <1.70,а) и (1.70,6) можно определить следующим образом:

м,=1п (1-ЬЫ-1п (1-Ы; (1,72)

2=1п(1-Е, )-1п(1-. ). (1.73)

Соответствие точек плоскостей и V17 показано на рис. 1.13,в, г. Проводя из точке 1 и а линии равного потока до верхней пластины конденсатора, получаем поверхность интегрирования:

S = ,uln

(1.74)

Напряженность электрического поля плоского конденсатора определяется по формуле

£ =W - (1-75)

Связь напряженности апектрического поля плоскости W с напряженностью плоскости t, устанавли-

Окончательно

вает выражение E = E,r(dwl(K,). женность электрического поля

напря-

(1.76)

Подставляя (1.7G) в (1.65), находим поле в любой точке плоскости Z.

Зная поле и поверхность поперечного сечения, можно легко найти мощность, передаваемую вдоль симметричного полоскового волновода. Так как поверхность интегрирования (1.74) определена для отображенной четверти симметричного волновода, выражение для передаваемой мощности будет иметь вид:

p.=v.\E,\d4.in\ - (1.77)

Для расчета максимальной передаваемой мощности необходимо учитывать неравномерность распределения напряженности электрического поля в плоскости поперечного сечения полоскового волновода, которая (по аналогии с несимметричным волноводом) учитывается коэффициентом Ос:

(йМ) (1 + Ш) р-bA/d)(4 + A/d)

полученным на основании формул (1.65) и (1.76).

Распределение напряженности электрического поля в поперечном сечении симметричного полоскового волновода представлено на рнс. 1.18.

В окончательном виде передаваемая по волноводу мощность определяется выражением

P ...= 2VijKEi (1 -ЬДW)(4+Д/й)X

Х1п

(1.79)

где £о - однородное электрическое поле между токонесущей полоской и заземленными пластинами; d-расстояние между ними; Д - толщина токонесущей полоски.