+ (2 + Jf + 2 (1 - cos а) - 2 (л^ + dJ2) (1

cos а) cos Ф1 - 22 K(cos2 cos а + sin? Фа) ((j + dJ2f. +

+ л§ (1 - cos а)2 - 2 (л^ + d/2) (1 - cos а) r cos Ф,) X

X cos

arctg

(Ла + dn/2) sin ф1

(лз + rfn/2) cos Ф1 - (1 - cosa)

- arctg

cosa

а=2я(т-l)/tt -угол между первым витком, принятым за начало отсчета, и т-м витком.

Приближенно можно считать, что индуктивность кольцевой катушки кругового сечения радиусом в 1,3 раза, меньше индуктивности кольцевой катушки квадратного сечения (см. рис. 2.12) со стороной 2б2=26з=2л2 при равенстве одноименных геометрических параметров 2. dn, г.

Пример 2.9. На кольцевом каркасе кругового сечения (рис. 2.14) радиусом /-2=4 мм и внутренним радиусом /-=8 мм намотана проводом диаметром dn=0,12 мм однослойная катушка с шагом h2 = =0,8 мм. Определить приближенное значение индуктивности катушки.

Решение. Найдем индуктивность кольцевой катушки квадратного сечения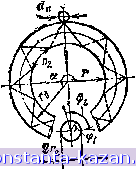

(см. рис. 2.12), стороны которого равны 2&2=2Ьз=2л2=8 мм. Геометрические раз-

Рис. 2.14. Геометрическая модель однослойной кольцевой катушки кругового сечения

меры г, Й2 и dn такой катушки совпадают с одноименными размерами кольцевой катушки кругового сечения.

Для bs/bi = 4/4 = 1, ribi = r/n = 8/4 = 2, Л2/62 = А2 -2=0,8/4=0,2 и dn/62 = rfn/ 2 = 0,12/4 = 0,03 по табл. 2.3 находим LKbiw ) =0,307мкГн/м, откуда

L = 622-0,307 = 0,004.63?-0,307 = 4,86 мкГн = 4860 нГн,

где П!>=2я/-/А2=2я8/0,8=63.

Индуктивность кольцевой катушки кругового сечения меньше

найденного значения приблизительно в 1,3 раза, т.е. I,r 4860/1,3 = = 3750 нГн.

2.4. ИНДУКТИВНОСТЬ СПИРАЛЬНЫХ КАТУШЕК

В параграфе приведены соотношения, номограммы и таблицы для расчета собственных индуктивностей спиральных катушек с кру-4*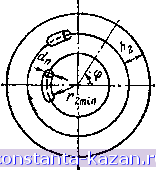

Рис. 2.15. Геометрическая модель однослойной спи-ральной катушки с круговыми витками

говыми, прямоугольными и равносторонними треугольными витками. Спиральные катушки с формой витков, близкой к правильным многоугольникам с числом сторон л 5, близки по своим свойствам к вписанным в них спиральным катушкам с круговыми витками и здесь не рассматриваются.

2.4.1. Спиральная катушка с круговыми витками

Индуктивность спиральной катушки с круговыми витками (рис. 2.15), имеющей шаг намотки Aj. диаметр провода dn, число витков w и ширину каркаса l=h2W (см. рис. 2.2),

ш-1 и)-1 я

L = iio

ft=0 т

Vim in

J Virmin + dn/2 + Лл m)? + (rmin + h k)-+ Л2 *) cos Ф dф

- 2 {rmin + dn/2 + fta m) {r.jnin + h k) cos ф

(2.18)

где timin - внутренний радиус минимального витка катушки; k, пг - порядковые номера витков катушки, причем первый внутренний виток принят за нулевой.

Формулу (2.18) можно представить в виде

am in

w-l ОУ-1 я

fc=0 m>=0 О

(1+0п/2 + Яат)(1 +

У(1+Я,;?)2 + (1+Л„/2 + Я2т)2 + Я2*)cosфdф -2(1 +Яг)(1+Оп/2 + Я2т)с05ф'

(2.19)

где W = J1IH2\ JI = t/rimln; Hi = h2lr2mln\ D = ddA2mfn -число ВИТКОВ

и геометрические размеры модели катушки.

Результаты расчета по (2.19) приведены на рис. 2.16, 2.17: сплошные линии -для dn/r2m;n=0,01 и 0,1; штриховые линии - для dnA2m/n=0,05 и 0,2.

Пример 2.10. Спиральная катушка с круговыми витками намотана проводом диаметром dn=0,l мм, имеет шаг намотки Ь^=\ мм и содержит ш=10 витков (см. рис. 2.15). Определить индуктивность

катушки, если внутренний радиус ее наименьшего витка Ггшгп= ,= 10 мм==0,01 м.

Решение. По кривой на рис. 2.16 (точка а) для значений

t/n/2m/n = 0,l/10 = 0,01, V2ni = 1/10 = 0,1 и 1/Г2т1п=1Ч1}кг/Г2тгп) =

.= (10-1)/10=1 находим Lft2/(2inm?) =3,96 мкГн/м, откуда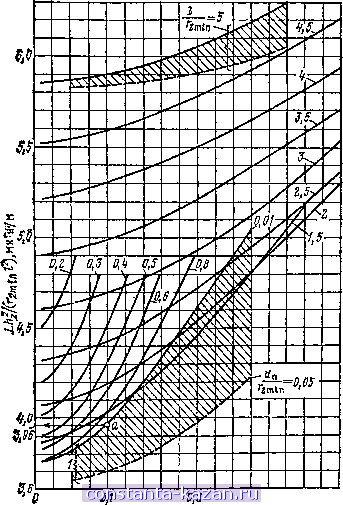

0,3 Jizhmin

Рис, 2.16. Зависимость собственной индуктивности спиральной ка-тушки по рис. 2.15 от ее геометрических размеров при dn/2min=0,01