Тогда общая формула (1.10) для расчета взаимной индуктивности в данном случае примет вид

(f) (f) i!!i±fiK ±L.( ==

у J а 4л J J а

I, h

л/2 л

b COS Ф2

COSфl

- COS Ф2

(3.5)

Bee приведенные в этой главе расчетные формулы определяют влаимную индуктивность по геометрическим моделям при одинаковом направлении обхода контуров и витков катушек. Поэтому взаимная индуктивность может иметь положительное и отрицательное значения.

3.2. ВЗАИМНАЯ ИНДУКТИВНОСТЬ ПЛОСКИХ КОНТУРОВ

в данном параграфе рассматриваются плоские круговые, прямоугольные и равносторонние треугольные контуры, а также двухпроводные длинные линии и различное их вза-пг.!ное расположение: соосное, концентрическое, эксцентрическое, с параллельными и пересека-Ю1ЦИМИСЯ осями. Плоские контуры в виде правильных многоугольников с числом сторон п^5 близки по своим свойствам к вписанным в них круговым контурам и здесь не рассмаг-р1гааются.

3.2.1. Соосное расположение плоских контуров

1. Взаимная индуктивность двух круговых контуров радиусами г Гг. расположенных соосно на расстоянии h (рис. 3.2),

Л1 =Цо

/-1 Ла cos ф4ф

о

]/ а2 + л2 + л2-2л, Л^СОЗф

(3.6)

М

Формулу (3.6) можно представить в виде л

Rx cos ф ф

0

о

. (3.7)

+/?] + 1-2 , cosф

Рис. 3.2. Геометрическая модель соосного расположения двух круговых контуров

где Я\ = г\/г2, Н=к/г2 - геометрические размеры модели. Результаты расчетов по (3.7) приведены на рис. 3.3.

Пример 3.1. Два круговых контура радиусами Г1=>10мм, Г2= = 5мм=0,005м и расположены соосно на расстоянии А=2,5 мм между их центрами (рнс. 3.2). Определить взаимную индуктивность контуров.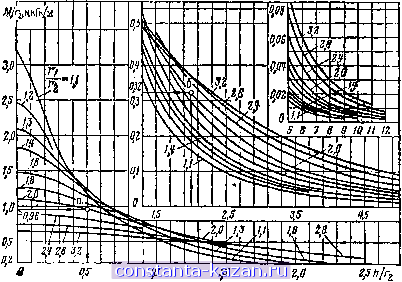

Рис. 3.3. Взаимная индуктивность двух соосно расположенных круговых контуров

Решение. Для значений /i/r2= 10/5=2 и ft/2=2,5/5=0,5 по рис. 3.3 (точка а) находим М/г2=0,9б мкГн/м, откуда взаимная индуктивность двух круговых контуров

М = гг-0,96 = 0,005-0,96 =

= 0,0048 мкГн = 4,8 нГн,

2. Взаи.мная индуктивность кругового контура радиусом г и равностороннего треугольного контура со стороной Ь, расположенных соосно на расстоянии h (рис. 3.4),

Рис. 3.4. Гео.метрическая модель соосно расположенных кругового и равностороннего треугольного контуров

я я/3

2а

ф|=0 ф2=0 Г

Ъг cos ф1 d(pt X

2 / 3 cos фа /

X ( Фг

6/- cos Фх

(3.8)

Уз cos фа

Результаты расчетов по (3.8) приведены на рис. 3.5.

пример 3.2. Круговой контур радиусом г=20 мм=0,02 м и равносторонний треугольный контур со стороной 6 = 40 мм расположены соосно (рис. 3.4). Определить взаимную индуктивность контуров, если расстояние между их центрами /г = 5 мм.

Решение. Для значений ЬД = 40/20 = 2 и V = 5/20=0.25 по рис. 3.5 (точка а) находим М/г=10,7 мкГн/м. откуда взаимная индуктивность кругового и равностороннего треугольного контуров

Л1=/-.10,7 = 0.02-10,7 = 0.214 мкГн = 214 нГн.

3. Взаимная индуктивность кругового контура радиусом г и прямоугольного контура со сторонами 26iX2b2, расположенных соосно на расстоянии h (рис. 3.6).

р

rbi cos Фх </фа

Ф,=0 ф,=0

COS фа

Я/2-Э

COS Фа гЬ cos Фх £(фа

+ h - 2

cos фа

cosфx

cos фа

cos фа

+ h.-2

cos фа

cos Фх

(3.9)

где Р = arctg-

Результаты расчетов по (3.9) приведены в табл. 3.1, а прн г/б2=3 представлены графиками на рис. 3.7.

Пример 3.3. Круговой контур радиусом г=15 мм и прямоугольный контур со сторонами 26i = 30mm и 22= 15 мм = 0,015 мм расположены соосно на расстоянии Л=7,5 мм (рис. 3.6). Определить взаимную индуктивность контуров.

Решение. Для значений 61/62 = 15/7,5 = 2, г/б2 = 15/7,5 = 2 и А/62=7,5/7,5=1 но табл. 3.1 определяем Л1/б2= 1,5 мкГн/м, откуда взаимная индуктивность кругового и прямоугольного контуров

Л1 = 6а-1,5 = 0,0075-1,5 = 0,01125 мкГн = 11,25 нГн.

4. Взаимная индуктивность кругового контура радиусом г и двухпроводной линии шириной 26, расположенных соосно на рас-