(3.11)

где ai=-64 cos a-63 sin a, fl2=b4Cosa-63 sin a, аз=-&4sina+ + bjcos a, 04=64sin a + 63cos a, fls=64C0S a-fcssin a, Oe=64COS a + + 6з31па, a7=64sin a-63cos a, H8=64sin а + 6зсоз a - пределы интегрирования.

6. Взаимная индуктивность двух прямоугольных контуров со сторонами 261X262 и 263X264, расположенных соосно и коаксиальио на расстоянии h между их центрами (рис. 3.10),

М

6. *.

р dxi dx

;io xj-b. ViPbi - bsf + (1 - + A? 63 ft,

pdyidyj

i,f=o 1/ (P 2 - b,) + (Ух - y,f + A* У

(3.12)

Если 0,3<62/6i<3 и 0,3<б4/6з<3, то приблизительно взаимная индуктивность контуров в 6264/6163 раз больше взаимной индуктив-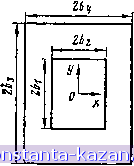

Рис. 3.10. Геометрическая модель соосного и коаксиального расположения двух подобных прямоугольных контуров

Рис, 3.11. Геометрическая модель общего случая соосного расположения прямоугольного контура и двухпроводной линии

ности двух соосно расположенных круговых контуров (см. рис. 3.2) радиусами/-1 = 61 и/-2=6 при прочих равных условиях. При одновременном сочетании значений b2/6i-*-0,3 и bi/bs-3 или 62/61-3 и bt/bs-0,3 точность приближенного расчета понижается.

Результаты расчетов по (3.12) для подобных прямоугольных контуров 61/62= 63/64 приведены в табл. 3.3.

Пример 3.5. Прямоугольные контуры со сторонами 26i=16 мм, 262=10 мм = 0,01 м, 26з=32 мм, 264 = 20 мм подобны и расположены соосно и коаксиально (рис. 3.10) на расстоянии между их центрами А=7 мм. Определить взаимную индуктивность контуров.

Решение. Для значений 61/62=8/5=1,6, 64/62=10/5=2 и А/62= = 7/5=1,4 по табл. 3.3 находим /И/б2=1,01 мкГн/м, откуда

М = 6g.l,01 = 0,005-1.01 = 0,00505 мкГн = 5,05 нГн.

7. Взаимная индуктивность прямоугольного контура со сторонами 261X262 и двухпроводной длинной линии шириной 26, расположенных соосно на расстоянии А так, что их плоскости симметрии пересекаются под углом а (рис. 3.11),

оо ь.

2л

Р dXi dx

р=±1 00 Хг

р dXi dx

pdyidy

- x tg aj -f A? .=-> у (у, - yf. + (pb -

b \a

+ i/ictga -I-/

(3.13)

sin a

8. Взаимная индуктивность двух двухпроводных длинных линий шириной 26 и 26 , расположенных соосно на расстоянии А так, что их плоскости симметрии пересекаются под углом а (рис. 3.12).

2л

р dxi dx

P=±I ДГ,=-00 JCj=-co

л/ {Xi-x,) + (pb--

f \ cos а

(3.14)

Если двухпроводные линии параллельны (а=0). то их взаимная ин-

-xxiga] +А=

Таблица 3.3. Взаимная индуктивность двух подобных прямоугольных контуров с коаксиальным расположением (рис. 3.10), отнесенная к геометрическому размеру М/бг, мкГн/м, при 61/62 = 63/64