Продолжение табл. 3.4

h/r.

-0,022

-0,056

-0,085

-0,108

-0,146

-0,149

-0,149

-0,146

-0,142

-0,13

-0,111

0,174 0,125 0,078 0,034 -0,007 -0,045 -0,079 -0,108 -0.131 -0,167 -0,17 -0,169 -0,166 -0,161 -0,148 -0,128

-0,009

-0,017

-0,041

-0,061

-0,099

-0.105

-0,109

-0.11

-0,11

-0.105

-0,095

0,162 0,124 0,087 0,052 0,019 -0,011 -0,038 -0,061 -0,081 -0,118 -0,124 -0,127 -0,128 -0,127 -0,122 -0,11

0,051 0,033 0,018 0,004 -0,028 -0,036 -0.042 -0,047 -0,05 -0.055 -0,057

0,139 0,117 0,095 0,074 0,054 0,036 0,019 0,003 -0,01 -0,042 -0,05 -0,056 -0,06 -0,064 -0,068 -0,069

0,065 0,053 0,042 0,032 0,007 0,0 -0,005 -0,011 -0,015 -0,022 -0,029

г\/г2 = Ъ

0,121 0,107 0,093 0,079 0,067 0,054 0,043 0.032 0,022 -0,003 -0,01 -0,016 -0.021 -0,025 -0.032 -0,038

0,065

0.059

0,053

0,048

0,033

0,028

0,024

0,02

0.017

0.01

0,002

0.094 0.087 0,08 0,074 0,067 0,061 0.055 0.049 0,043 0.028 0,023 0,019 0.015 0.011 0,005 -0.002

0,056 0,053 0,049 0.046 0,037 0,034 0,031 0,028 0,028 0,021 0,015

0,075 0,071 0,067 0,063 0,059 0.055 0,052 0,048 0,045 0,035 0,032 0,029 0,026 0,024 0,019 0,012

0,046

0,044

0,042

0,04

0,034

0,032

0,03

0,028

0.027

0,023

0,019

0,06

0,058

0,055

0,053

0,05

0,048

0,045

0,043

0,041

0.034

0,032

0.03

0.029

0.027

0.023

0.018

Рис. 3.15. Геометрическая модель расположения двух круговых контуров с параллельными осями

где при sri

а = у^Я^ + rI + I+S - 2R S cos ф, + 2x

1 / ,., 9 / У?, sin ф|

XVS+R\-2RScosФ, cosФ, + arctg j-

R\=i\/i2, S = s/r2 И H=h/r2 - геометрические ра.змеры модели.

Результаты расчетов по (3.19) приведены в табл. 3.4, а для л,/л2=1 - на рис. 3.16.

Если круговые контуры расположены в одной плоскости, то их взаимная индуктивность определяется по (3.18) при /i = 0. Результа- ты расчетов по (3.19) для этого случая приведены на рис. 3.17: сплош-

НаЯ линия - при 5>Л1+Л2 и штриховая линия - при 5<Л1+Л2.

Пример 3.8. Два круговых контура радиусами ri = 10 мм, Л2= = 5 мм = 0,095 м расположены на параллельных плоскостях, расстояние между которыми ft=3 мм (рис. 3.16). Определить взаимную индуктивность контуров, если расстояние между их осями s= 17,5 мм.

Решение. Для значений л,/Л2=10/5 = 2, /г/Л2=3/5=0,6 и 5/ла= 17,5/5 = 3,5 по табл. 3.4 находим М/г2 =-0,111 мкГн/м, откуда взаимная индуктивность двух круговых контуров

М =-/-2.0,111 =-0,005.0,111 =-0,555.10-3 мкГн =-0,555нГн.

2. Взаимная индуктивность кругового радиусом л и прямоугольного со сторонами 2biX2&2 контуров, расположенных симметрично относительно плоскости АВ, как показано на рис. 3.18, о сплошной линией.

М

t 1 JS

pr(s + pbx) cos 4>iX

ф;=оф,=о, =±1 l/ /J±PbY + ,2 + fta 2,x

V \ cos Фа;

X d(px d(f2 { f rb cos Ф1 X

Х^:со ф1 .=0> =v.sinфз/ (

cos ф.2 V \ sin фз

Xdjdi

+ a? + Л2 -

- 2-cos ф,

sin Ф2

(3.20)

bi 62

где P = arctg-;-- ; = arctg --- ; V2 = arctg .

s + pb, s-\- b, s- bl

Формула (3.20) справедлива для любых значений s-&i>0. Расчет взаимной индуктивности кругового и прямоугольного контуров с параллельными осями можно свести к рассмотренному выше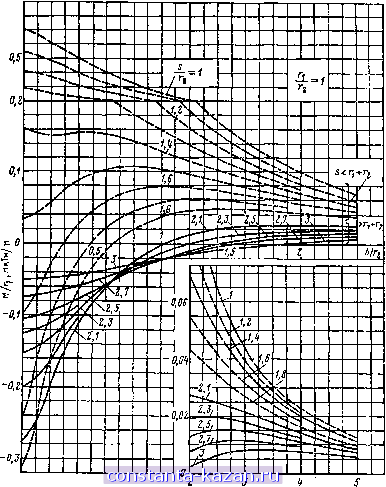

Рнс. 3.16. Взаимная индуктивность двух круговых контуров с параллельными осями при Гу1Г2=\

случаю соосного расположения контуров. Для этого дополним заданный прямоугольный контур / прямоугольным контуром 2 и прямоугольным контуром 3, равным контуру 1, образующими в совокупности соосно расположенный с круговым контуром прямоугольный контур 1-\-2-\-3. Взаимная индуктивность кругового контура и прямоугольного контура / равна полуразности значений взаимной индуктивности соосно расположенных круговых контуров и двух прямо-