26 = 21 Са sin ct - 6 cos а I = 2

= 10 MM,

расположенных соосно с круговым контуром на расстояниях

12 V2

hi = 6 sin ct + Cl - Са cos а = 5-г + 15 - 10 --3- = 10 мм;

= I Cl - Са cos а - 6 sin ос I =

V2 V2

15-10--5-

V2 V2

= 0.

Для этого по табл. 3.2 для значений Л'Д = 15/5 = 3, 6 /- = 5/5= 1, hr = 10/5 = 2 и /la/r = 0/5 = О

определяем Afi/f=0,29 мкГн/м и Мг/г = 2,Ъ2 мкГн/м, т. е. взаимные индуктивности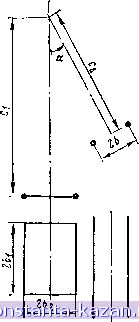

Рис. 3.35. Геометрическая модель расположения двухпроводной линия я кругового контура с пересекающимися осями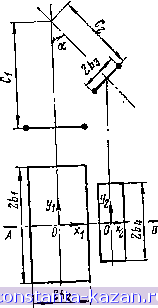

Рис. 3.36. Геометрическая модель расположения двух прямоугольных контуров с пере-сскающимкся осями

Mj = r-0,29 = 0,005.0,29= 1,45-10-3 мкГн = 1,45 нГн;

Ma = r.2,32 = 0,0C5.2,32=ll,6.10-3 мкГн= 11,6 нГн.

Искомая взаимная индуктивность кругового контура и двухпроводной линии равна полуразности полученных значений:

М = (Ml - М^)12 = (1,45 - 11,6)/2 =-5,075 нГн.

4. Взаимная индуктивность двух прямоугольных контуров со сторонами 261X262 и 263X264, расположенных симметрично относптельно плоскости АВ так, что их оси пересекаются под углом а (рис. 3.36),

М

V(Pi b,-bir + (x,-x,+

+ tj sin a)2 -f (ci - Cj cos (x + x tga)*

Pl Pa dyi dy

V(Pi S cos a -62 + Ca sin af-Hyi -1/2)+

5. Взаимная индуктивность двух контуров, расположенных на кольцевом каркасе с внутренним радиусом г и прямоугольным поперечным сечением со сторонами 26i X 262 (рис. 3.37),

-f (сх - cos а -f Pl 63 sin а)? j

(3.29)

p=±l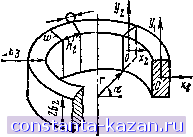

I P dy dy

\V{yi-yt) + lr + 2h-

Рис. 3.37. Геометрическая модель расположения контуров на кольцевом каркасе с прямоугольным поперечным сечением

-(r+(p + l)hi)cosa\ + (r + (p + l)b-if sina

Pdy dy

У(У1-УгУ+[г -(r-(P - !) S) cos aP +(r-(p-l) bf sina

&,cos а

р cos к dXj

x,=-b, Xi=-bi cosa

V [Xx - a + + - cos a)]? +

+[(r + 6) sin a + tg a]2 + (p - 1 )2 6

(3.30)

где a - угол между плоскостями расположения контуров.

Результаты расчетов по (3.30) приведены в табл. 3.6 и представлены графиками на рис. 3.38.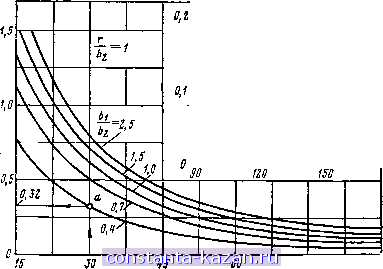

15 а, град

Рис. 3.38. Взаимная индуктивность двух контуров, расположенных на кольцевом каркасе с прямоугольным поперечным сечением при

ri/U2=l

Пример 3.18. Два контура расположены на кольцевом каркасе с внутренним радиусом г=10 мм и прямоугольным поперечным сечением со сторонами 26i = 8 мм и 22=20 мм = 0,02 м (рис. 3.37). Определить взаимную индуктивность контуров, если угол между плоскостями их расположения а = 30°.

Решение. Для значений г/б2= 10/10=1 и 6i/62=4/10=0,4 из рис. 3.38 (точка а) находим М/б2=0,32 мкГн/м, т. е. искомое значение взаимной индуктивности

M = 6a.0,32 = 0,01-0,32=3,2-10-з мкГн = 3,2 нГн.