Таблица 3.6. Взаимная индуктивность двух контуров, расположенных под углом а на кольцевом каркасе прямоугольного сечения (рнс. 3.37), отнесенная к геометрическому размеру M/bj, мкГн/м

I 1.5 I 2 I 2,5

30 45 60 75 90

0,119

0,047

0,023

0,013

0,009

0,157

0,063

0,031

0,018

0,013

0,669 0,227 0,095 0,048 0,029 0.02

0,861

0,309

0.135

0.07

0.043

0,031

1.08

0.393

0.182

0,098

0.063

0,047

1,21

0,449

0,211

0.118

0,078

0,06

15 30 45 60 75 90

0,232

0,056

0.02

0,009

О 005

0,003

0.305 0,077 0.028 0.012 0.007 0.005

0,436 0.119 0.044 0.021 0,012 0.008

0,597 0.176 0.068 0.032 0,019 0.013

0,787

0.247

0,05

0,03

0,022

0,91

0,293

0,123

0,064

0,04

0,029

15 30 45 60 75 90

0,145

0,030

0,01

0,004

0,002

0,0016

0,197 0.042 0,014 0,006 0,003 0,002

0,298

0,069

0,024

0,01

0,006

0,004

0,429

0,108

0,038

0,017

0,01

0,007

0,594 0.162 0,061 0,029 0,017 0,012

0,707 0,201 0,079 0,038 0,023 0,017

30 45 60 75 90

0,096

0,018

0,0057

0.0024

0,0013

0,001

0,134 0,026 0,008 0,003 0,002 0,0013

0.211 0,043 0.014 0,006 0,003 0,002

0,317

0,07

0,023

0,01

0,006

0,004

0.457

0,111

0,039

0,018

0,01

0,007

0,559 0,144 0,053 0,025 0,015 0,01

15 30 45 60 75 90

0,066

0,011

0,0035

0,0015

0.0008

0,0005

0.094

0,016

0,0052

0,0022

0,0012

0,0008

0,153

0,028

0,009

0,004

0,0021

0,0014

0,239 0,048 0,015 0,006 0,003 0,0025

0,358 0,079 0,027 0,012 0,007 0,0047

0,449

0,106

0,037

0,017

0,01

0,007

3.2.6. Общий случай

Для расчета взаимной индуктивности двух плоских контуров произвольной формы, произвольно расположенных в пространстве относительно друг друга, необходимо воспользоваться (1.10) в общем виде.

Если площади произвольных контуров можно представить как суммы площадей простых контуров (круг, прямоугольник, равносторонний треугольник), то взаимная индуктивность двух произвольных контуров будет равна сумме взаимных индуктивностей каждого простого контура, расположенного в одном произвольном контуре, и всех простых контуров, расположенных в другом произвольном контуре. Таким образом, расчет взаимной индуктивности двух произвольных плоских контуров можно свести к расчету взаимных индуктивностей простых плоских контуров, рассмотренных выше.

Пример 3.19. Сложный контур и двухпроводная линия шириной 26 = 66 мм расположены в параллельных плоскостях, расстояние между которыми А=105 мм, симметрично относительно плоскости АВ (рис. 3.39). Определить взаимную индуктивность контура и линии.

Решение. Представим сложный контур двумя простыми контурами; контуром 1, составляющим половину кругового контура радиусом г=30 мм, и прямоугольным контуром 2 со сторонами 26iX262=100X ХбОмм. Взаимные индуктивности контура / и двухпроводной линип и контура 2 и двухпроводной линии определены в примерах 3.4.3.7 и равны Л1,= 1,47 нГн, M2 = 6,l нГн.

.Zbz

Рис. 3.39. Геометри. ческая модель взаимного расположения двухпроводной линии и сложного контура

Взаимная линии

индуктивность сложного контура и двухпроводной М = Mi + = 1,47 + 6,1 = 7,57 нГн.

3.3. ВЗАИМНАЯ ИНДУКТИВНОСТЬ КАТУШЕК И ПЛОСКИХ

КОНТУРОВ

Формулы для расчета взаимной индуктивности при различной форме плоских контурод и катушек получены на основе суммирования взаимных индуктивностей плоского контура и каждого витка катушки. Витки катушки в свою очередь также представляются в виде плоских контуров.

Ниже рассматриваются однослойные цилиндрические и прямо-

§ 3.3

Взаимная индуктивность катушек и контуров

угольные катушки, магнитно связанные с плоскими круговыми или прямоугольными контурами, а также с двухпроводной линией, как наиболее простые для математического описания. Для нахождения взаимной индуктивности при соосном расположении контура и катушки, а также при параллельности их осей приводятся номограммы и таблицы В других случаях расположения контура и катушки приводятся только расчетные формулы для определения взаимной индукции по математическим моделям.

3.3.1. Соосиое расположение катушек и плоских контуров

1. Взаимная индуктивность однослойной цилиндрической катушки радиусом Г2, длиной /, шагом намотки Лр, числом вптков ш= Л2 и кругового контура радиусом г\, расположенных соосно (рис. 3.40, поз. /) и согласно 1=0),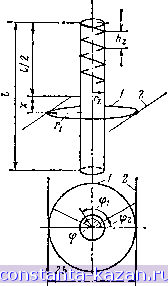

о

Гх COS ф Йф

Рис. 3.40. Геометрическая модель соосного расположения однослойцой цилиндрической катушки и кругового контура (/) или двухпроводной линии (2)

{kh,f + r\ + rl-2r гзсозф

(3.31)

где Мв.к - взаимная индуктивность, определяемая по (3.6) к-то витка катушки и контура, расстояние между центрами которых равно h=kh2; номер витка, расположенного в плоскости контура, принят за нулевой.

Формула (3.31) справедлива для любых значений rKriKr. Результаты расчетов по (3.31) приведены на рис. 3.41: сплошные линии для ri/2=l,l, а штриховые и штрихпунктирные линии для ri/r2=l,2; 1,3; 1,4. Из рис. 3.41 видно, что в диапазоне 0</12/г2<:1 при Г\/Г2>->1,2 величина МНЦЫ) изменяется не более чем на 10-15%, причем тем меньше, чем больше отношение ri/r?.

С учетом практического постоянства величины Mh2l{r2l) для этого случая в табл. 3.7 приведены ее значения при hijri-0,1.

Если />2(Г|-1-2г2), то взаимная индуктивность катушки и кругового контура мало зависит от отношения Г|/л2 (рис. 3.42, поз 1), Это объясняется особенностями характеристик взаимной индуктивности соосно расположенных круговых контуров (см, рис. 3.3). Дей-8- 60