Продолжение табл. 3.11

46.1 44,5 42.8 38,8 35.1 31,6 28,4 25,5 20,6 16.7 11,2 7,82 5,61 4,14 3,13 1.91 1.25

52.4 50,6 48.8 44.3 40,1 36.2 32.7 29,5 23,9 19,5 13,3 9,34 6,76 5,04 3.76

40,1 38.8 37,5 34,3 31,2 28,3 25,7 23,2 19

15,6 10,6 7,51 5,43 4,03 3,07 1 ,88 1.23

46 44.5 43.1 39.4 35,9 32.7 29.7 26.9 22,2 18.3 12,6 8.99 6,56 4.91 3,68

35,1 34,1 33 30,4 27,9 25,5 23,2 21,1 17,5 14,5 10,1 7,19 5,25 3,92 3

1,85 1,22

40,5 39,4 38,2 35,2 32,3 29,6 27

24,6 20.5 17,1 12

8.63 6.35 4,78 3.51

20,7 20,3 19,9 18,9 17,8 16,8 15,8 14,8 13

11,3 8,64 6,61 5,1 3,99 3,16

с параллельными осями расположены несогласно, то их взаимная индуктивность равна при 0х<1/2 полусумме (при д:> 2 -полуразности) взаимных индуктивностей двух однослойных цилиндрических катушек длиной /, = / + 2д; и h=l-2x (li = l + 2x и l2=2x-l), каждая из которых расположена согласно с круговым контуром.

Пример 3.25. Однослойная цилиндрическая катушка радиусом / j=10 мм = 0,01 мм, длиной /=30 мм и с шагом намотки Л2=1 мм и круговой контур радиусом ri = 20 мм имеют параллельные оси, расстояние между которыми s=40 мм (рис. 3.47, поз. /), Определить взаимную индуктивность контура и катушки при их согласном {х=0) и несогласном {х=5 мм) расположениях.

Решение, а) Согласное расположение, х=0.

По табл. 3.11 для значений г,/г2=20/10=2, s/r2=40/10=4, Г2=30/10 = 3 и Л2/Г2= 1/10=0,1 определяем iMAj/W) =65,6х XIO-* мкГн/м, т.е. взаимная индуктивность кругового контура и однослойной катушки

I 30

Л1 = А -- 65,6-10-з = 0,01-- 65.6-10-з =

= 0,0196 мкГн= 19,6 нГн, б) Несогласное расположение, х=5 мм.

Определим вначале взаимную индуктивность кругового контура и двух согласно расположенных с ним однослойных катушек длиной /i = /+2;е=30 + 2-5=40 мм, /2=/-2;е=30-2-5=20 мм.

По табл. 3.11 для значений /,/г2=40/10=4 и /2/2=20/10=2 при 5/г2=40/10 = 4, Лг/гг* 1/10=0,1 и г,/г2=20/10=2 находим MM{r,li) = 52,4-10-3 = мкГи/м и М-МПггк) = 81,2-10- мкГи/м, т. е. взаимные индуктивности

Ml =Лг~- 52,4-10-3 = 0,01 - 52,4.10-3 =

rtjj 1

= 0,02096 ккГн = 20,96 нГн;

/ 20

М, = лз- 81,2.10-3 = 0,01--81,2.10-8 = ftj 1

= 0,01624 мкГн= 16,24 нГн.

Взаимная индуктивность однослойной цилиндрической катушки и кругового контура, расположенных несогласно,

/И = (/И, -4- Л1а)/2 = (20,96 + 16,24)/2 = 13,6 нГн.

2. Взаимная индуктивность однослойной цилиндрической катушки радиусом Гг, длиной f и с шагом намотки и двухпроводной линии шириной 2b с расстоянием между их параллельными осями S (рис. 3.47, поз. 2) равна при s-Ь>Г2 полуразности (при b~s> >Г2 - полусумме) взаимных индуктивностей этой катушки и двух соосно расположенных с ней двухпроводных линий шириной 2Ь' = = 2(s + 6) и 26 =2s-b\. Методика расчета взаимной индуктивности однослойной цилиндрической катушки и двухпроводной линии при соосном расположении приведена в п. 3.3.1.

Пример 3.26. Однослойная цилиндрическая катушка длиной

2=50 мм, радиусом Г2=10 мм = 0,01 м и с шагом намотки /12= 1 мм расположена несоосно (s = 30 мм) и согласно {х=-0) с двухпроводной линией шириной 26=20 мм (рис. 3.47, поз. 2). Определить взаимную индуктивность катушкн и двухпроводной линии.

Решение. Определим вначале взаимную индуктивность однослойной цилиндршеской катушки и соосно расположенных с ней двух двухпроводных линий шириной 26 = 2(s + 6) =2(30+10) = = 80 мм и 26 =2s-&1=2 (30-10) 1=40 мм. По табл. 3.8 для значений Ь7г2=40/10=4 н Ь /г2=20/10 = 2 при ? -2=50/10=5 и Vs = 1/10=0,1 находим Ali/i2/(r20 = 0,288 мкГи/м и Mih2/(r2l)= = 0,463 мкГн/м, т.е. взаимные индуктивности

I 50 All = Га - 0,288 = 0,01 - 0,288 = 0,144 мкГн = 144 нГн;

М^ = г^- 0,463 = 0,01 - 0,463 = 0,231 мкГн=231 нГн.

в рассматриваемом случае s-6 = = 30-10=20>/-2=10 мм. Поэтому искомая взаимная индуктивность

М = (Ml - М^)/2 = {144 - 231 )/2 =

=-43,5 вГн.

3.3.3. Эксцентрическое расположение катушек и плоских контуров

1. Взаимная индуктивность однослойной цилиндрической катушки длиной /, с шагом намотки hi, числом витков г£ = = l/hi и радиусом и кругового контура радиусом п, расположенных эксцентрически под углом а между их осями (рис. 3.51, поз. 1) и согласно (дс=0), ai/2

М

2 м

(3.36)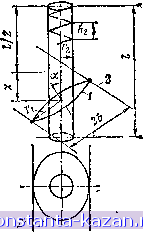

PiiC.

где Л1в,к - взаимная индуктивность й-го витка катушки и кругового контура, определяемая по (3.27) при Ci = 0 и С2= =Й2; номер центрального витка катушки принят за нулевой.

Формула (3.36) справедлива для любых значений г^КпКГг.

Если круговой контур и однослойная цилиндрическая катушка расположены несогласно, то их взаимная индуктивность равна при 0<х< 2 полусумме (при х> 2 - полуразности) взаимных индуктивностей двух однослойных цилиндрических катушек длиной /[ =

3.51. Геометрьчёс-модель эксцентрического расположения однослойной цилиндрической катушки и плос* кого контура:

2 - то же. что на риа. 3.42