=/ + 2je и l2l-2x {li=l+2x и l2=2x-l), каждая из которых раст положена согласно с круговым контуром.

2. Взаимная индуктивность однослойной цилиндрической катушки и двухпроводной линии, расположенных эксцентрически (рис. 3.51, поз. 2) и несогласно (хфО), равна полусумме взаимных индуктивностей этой катушки и двух одинаковых двухпроводных линий шириной 2& = 2&cos(p, каждая из которых расположена с катушкой соосно (рис. 3.40, поз. 2) и несогласно на расстояниях Ari=JC+isina и х2=\х-bsinaj.

Пример 3.27. Двухпроводная линия шириной2Ь=2У 5+20 мм и однослойная цилиндрическая катушка с шагом иамотки ft2=l мм, длиной /=50 мм и радиусом Г2=10 мм расположены эксцентрически

под углом a = arccos-izzZT между их осями (рис. 3.51, поз. 2)

Vb + 20

и согласно х-0. Определить взаимную индуктивность двухпроводной линии и катушки.

Решение. Заменим данную двухпроводную линию двухпроводной линией шириной 2b=2b cos а= (2/ 52-f202.2o)/K52-f20= = 40 мм, расположенной с катушкой соосно и несогласно на расстоянии x = 6sina=(K52--20?.5)/l/52--20? = 5 мм (рис. 3.40, поз. 2).

Взаимная индуктивность двухпроводной линии и катушки определена в примере 3.21 и равна Л1 = 228,4 нГн. Такое же значение взаимной индуктивности будет для эксцентрического расположения катушки и двухпроводной линии.

3.3.4. Катушки и плоские контуры с пересекающимися осями

1. Взаимная индуктивность однослойной цилиндрической ка-тушки длиной /, с шагом Лг, числом витков w = l/h2 и радиусом га и кругового контура радиусом гу, расположенных согласно (дг=0) так, что их оси пересекаются под углом а (рис, 3.52, поз. 1),

се>/2

М= 2 Мв,к. (3.37)

k=-w/2

где взаимная индуктивность Мв,к k-ro витка катушки и кругового контура определяется но (3.29) при C2=Ci cos а-нМ; номер центрального витка катушки принят за нулевой.

Если круговой коитур и однослойная цилиндрическая катушка с пересекающимися осями расположены несогласно, то их взаимная индуктивность равна при 0<х< 2 полусумме (при х>1/2-полуразности) взаимных индуктивностей двух однослойных цилиндрических катушек длиной li=l + 2x и h=t--2x {l\ = l-2x и h=2x-l), каждая из которых расположена согласно (с=0) с круговым контуром при прочих равных условиях.

2, Взаимная индуктивность однослойной цилиндрической катушки и двухпроводной линии шириной 2& с пересекающимися под углом а осями (рис. 3.52, поз. 2) в общем случае {х'О) равна при Cisina>6cosa полуразиости (при с, sin а<Ь cos а - полусумме)

Рис. 3.52. Геометрическая модель расположения однослойной цилиндрической катушки и плоского контура с пересекающимися осями:

/ и 2 - то же, что на рис. 3.42

взаимных индуктивностей этой катушки и двух двухпроводных линий шириной 2Ь' = =2(с, sina + bcosa) и 2Ь = = 2ci sina-6 cosa[, расположенных относительно нее соосно (рис. 3.40, поз. 2) и несогласно на расстояниях х\=х+ -ьЬ sin а идс2=дг-Ь sin а|. Методика расчета взаимной нн-дуктивности для этого случая рассмотрена в п. 3.3.1.

3.3.5. Общий случай

Рассмотренные выше методы расчета взаимных индуктивностей однослойных цилиндрических катушек н круговых

контуров при их различных взаимных расположенпях справедливый для других форм сечений однослойных катушек п плоских контуров. Действительно, выражения взаимных индуктивностей Л/а,к (3.33) - (3.37) одного плоского витка однослойной катушки и плоского контура справедливы при любой форме плоских фнгур. Для наиболее распространенных на практике форм сечения однослойных катушек

и плоских контуров выражения для взаимной индуктивности Мв.к

можно заимствовать из § 3.2.

Взаимная индуктивность многослойной катушки и плоского контура определяется как сумма взаимных индуктивностей плоского контура и каждого слоя катушки.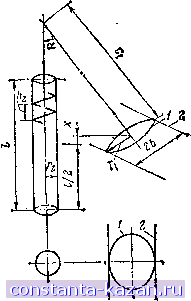

3.4. ВЗАИЛ1НАЯ ИНДУКТИВНОСТЬ КАТУШЕК

Формулы для расчета взаимных индуктивностей различно расположенных катушек с различной формой поперечных сечений получены на основе суммирования взаимных индуктивностей каждого витка одной катушки и всех витков другой катушки, причем витки обеих катушек представляются плоскими. Ниже рассмотрены однослойные цилиндрические и прямоугольные катушки с параллельными осями и соосным расположением, как наиболее простые для математического описания. Приведены справочные номограммы и таблицы.

3.4.1. Соосное расположение катушек

I. Взаимная индуктивность двух однослойных цилиндрических катушек радиусами ri, гг, с одинаковым шагом намотки Лг, одинаковой длины / и с числом витков w = l/h2, расположенных соосно (рис. 3.53) и согласно {х=0),

w w

с 10,0 гх COS ф d(p

ш w 3

V 1(=1 - + ri + rl-2r,r cos ф

, (3.38)

где Мв,в-определяемая по (3.6) взаимйая индуктивность двух витков катушек, расположенных на расстоянии h=\ki-212 вдоль осей; А, и 2 - порядковые номера витков катушек.

Результаты расчетов по (3.38) приведены на рис. 3.53. Из графиков видно, что в диапазоне 0<Л2Д2<0,8, при r\lri\,2 величина Mh\l[rf изменяется не более чем на 10 %. С учетом практического постоянства величины Mh\l(r2l) для этого случая в табл. 3.12 приведены ее значения при Л2 -2=0,1.

При различном шаге намотки катушек ЬцФНцг) их взаимная индуктивность изменяется в А2(п/Л2(2) раз относительно случая, когда пх шаги намоток одинаковы (/J2(i) = ft2(2)) при прочих равных геометрических размерах*.

Пример 3.28. Две однослойные катушки одинаковой длины I - = 40 мм с радиусами ri = 15 мм, Г2=10 мм=0,01 м расположены соосно и согласно (рис. 3.53). Определить их взаимную индуктивность при шаге намотки /i2(i)=A2(2) = l мм и Агп) = 1 мм, Л2(2) = 2мм.

Решение, а) Одинаковый шаг намотки, Агсп -2(2) = ! мм.

Для геометрических размеров ri/r2= 15/10= 1,5, Л2(п/г2=Л2!2)/г2 = = 1/10=0,1 и ;/г2=40/10 = 4 по табл. 3.12 находим Mhl/{r2f) = = 0,705 мкГн/м, т.е. взаимная индуктивность катушек

/2 402

М --0,705 = 0,01 ---0,705= 11,28 мкГн = 11 283 нГи.

>

б) Различный шаг намотки, Л2(1> = 1 мм, Л2(2)=2 мм.

Взаимная индуктивность катушек изменится в ft2(i) i2(2) = 1/2= = 0,5 раза относительно взаимной индуктивности при одинаково.м шаге намотки ft2(i)=A2(2) = 1 мм, т.е.

М = 0,5.11 280 = 5640 нГн,

* Здесь и далее при обозначении однотипных параметров с индексами номер катушки дается в скобках.