1,5 2

3,79 2,72 2,02 1,34 0,814

2,71 2,2 1,77 1,26 0,795

2,11 1,81 1,54 1,16 0,768

1,73 1,54 1,34 1,06 0,736

1,47 1,33 1,19 0,977 0,702

1,27

1,17

1,07

0,898

0,667

1,12

1,05

0,965

0,828

0,635

1,01

0,946

0,879

0,767

0,601

0,912 0,862 0,807 0,714 0,571

0,833 0,791 0,746 0,667 0,543

0,709

0,68

0,647

0,588

0,493

0,618

0,595

0,57

0,526

0,451

0,547

0,53

0,51

0,475

0,414

0,t91 4,477 0,461 0,432 0,383

0,445 0,434 0,421 0,397 0,355

b,/b2 = 2,2

0,513

0,485

0,457

0.409

Ь,/&2=2,5

Если отношение сторон прямоугольных катушек лежит в пределах 0,3<b2/b,<3 и 0,3<b4/i7j<3, то их взаимная индуктивность примерно в bib/bibs раз больше взаимной индуктивности двух соосно расположенных цилиндрических катушек (рис. 3.53) радиусами ri = bi, Tibz при прочих равных размерах.

Результаты расчетов по (3.43) для подобных прямоугольных однослойных катушек bjbibs/bt, fi = /a = /, А2(1)=А2(2)=Л2, расположен-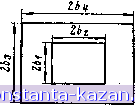

Рис. 3.56. Геометрическая модель соосного и согласного расположения двух однослойных катушек с подобными прямоугольными сечениями

ных соосно и согласно (рис. 3.56) при /12/62=0,!, приведены в табл. 3.13. В диапазоне 0</г2/б2<0,5 при bi/b2>l,l величина Mhl/{b2P) практически остается постоянной (см. аналогичные характеристики на рпс. 3.53).

Если шаг намотки однослойных прямоугольных катушек различен {?!2(i)=7/i2(2)),TOHx взаимная индуктивность изменится в A2(i, i2(2) раз относительно случая, когда кц\) = кт) при прочих равных размерах.

Расчет взаимной индуктивности при несогласном расположении двух катушек можно свести к расчету системы согласно расположенных катушек подобно описанному в п. 3.4.1, пп. 2.

Пример 3.30. Две однослойные прямоугольные катушки равной длины /=30 мм и с одинаковым шагом намотки /12= 1 мм пмеют подобные прямоугольные поперечные сечения б1 72=13/10=Ьз/б4 = 26/20 и расположены соосно и согласно (рис. 3.56). Определить взаимную индуктивность катушек.

Решение. Для геометрических размеров /7,/62=13/10=1,3, Vb2= 1/10 = 0,1, 62 = 30/10=3 и 64/62=20/10 = 2 по табл. 3.13 находим Mh\/{b2l)=\,\ мкГи/м, т.е. взаимная индуктивность катушек

/И = 6., 4- 1.1 = 0,01 -4т 1.1 = 9,9 мкГн = 9900 нГн.

4. Взатшная индуктивность однослойных цилиндрической радиусом г и прямоугольной со сторонами 261X262 катушек с равными шагами намотки кг, длиной / и числами витков w = l/h2, расположен-

(3.44)

ных соосно (рис. 3.57) и согласно,

w w

где Aia.B - определяемая по (3.9) взаимная индуктивность двух витков катушек, расположенных на расстоянии h=\ki-k2\h2 вдоль осей; kx li ki - порядковые номера витков катушек.

<S3

Рис. 3.57. Геометрическая модель соосного и согласного расположения однослойных цилиндрической и прямоугольной катушек

Результаты расчетов по (3.44) при 2/62=0,! приведены в табл. 3.14 и справедливы для значений 0</г2/б2<0,5, так как величина А1А2/(Ь2) изменяется при этом не более чем на 10 %.

Расчет взаимной индуктивности катушек при несогласном расположении сводится к расчету системы согласно расположенных катушек по описанной в п. 3.4.1, пп. 2 методике.

Взаимная индуктивность катушек с различными шагами намотки 2(i)9/i2(2) изменится в /г2(1)/Й2(2) раз оЛосительно случая A2(i) = =Л2(2) при прочих равных размерах.

Пример 3.31. Однослойные катушки цилиндрическая радиусом г - Ъ мм и прямоугольная со сторонами 2bi=40 мм и 2&2=20 мм = =0,02 м имеют равные длины ( = 50 мм и шаг намотки мм

и расположены соосно п согласно (рнс. 3.57). Определить взаимную индуктивность катушек.

Решение. Для геометрических размеров г/Й2 = 5/10 = 0,5, 61/62=20/10 = 2, 62 = 50/10 = 5 и /12/62= 1/10 = 0,1 из табл. 3.14 следует M/i2/(62p) =0,148 мкГн/м, т.е. взаимная индуктивность катушек

Л1 = 6,- 0,148 = 0,01 -- 0/,148 = 3,7 ккГн = 3700 нГн.

3.4.2. Катушки с параллельными осями

1. Взаимная индуктивность двух однослойных ц::л!шдрическич катушек одинаковой длины /, с шагом намотки и числом витков wl/hi, радиусами гь Г2 и расстоянием s между их параллельными осями при сОггсном расположении (рис. 3.58)