§ 1.4

Эффект близости

В общем случае все эквивалентные параметры витков зависят от частоты тока, а также от удельной электрической проводимости материала витков и их геометрии.

1.4. ЭФФЕКТ БЛИЗОСТИ

Использование понятия элементарного замкнутого витка позволяет учитывать специфические явления, возникающие при близком расположении друг к другу проводников с током. Эти явления получили название эффекта близости.

Рассмотрим в качестве примера эффект близости в двухпроводной линии. На рис. 1.6 приведено взаимное расположение проводников двухпроводной линии в виде плоских шин, к которой подключен источник напряжения е(/). Представим обе шины в виде совокупности элементарных шин, по каждой из которых протекает ток Дг. Если напряжение источника имеет синусоидальную форму с угловой частотой со, то распределение тока по поперечному сечению шин будет определяться системой уравнений (1.18), в которой значение взаимной индуктивности k-Pi и т-й элементарных шин на единицу длины определяется формулой (1.11). Эта общая формула в данном случае примет вид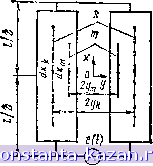

Рис. 1.6. Геометрическая модель для расчета эффекта близости в двухпроводной линии с плоскими шинами

dxkdxr,

ь=Одс =- 2

dXk dXra \

V (Xk-Xmf + (yh+ymY- ! 2 2

У{Хк-Хт)-{Ук-рУтГ

где / - длина шин; ук, Ут - /а ширины k-Ъ и /и-й элементарных шин; dxk, dxm - элементы длины элементарных шин; р=±1 - параметр суммирования, принимающий два целочисленных значения*.

Взаимная индуктивность Mkm зависит от расстояния между ши-

* Применение параметров суммирования позволяет сократить запись расчетной формулы и будет широко использоваться в дальнейшем.

нами. Поэтому распределение тока по сечению шин, а также их собственная индуктивность на единицу длины, определяемая по (1.15), будут зависеть от взаимного расположения шин. На рис. 1.6 показан характер распределения плотности тока по сечению плоских шин. Наибольшее значение плотность тока достигает на внутренней границе шин, что объясняется наименьшим значением потокосцепления с расположенной на этой границе элементарной шиной.

1.5. ВЛИЯНИЕ ШАГА НАМОТКИ КАТУШЕК

Одним из трудно учитывае.мых факторов при расчете катушек без магнитных сердечников является шаг намотки витков, если ои соизмерим с размерами поперечного сечения каркаса. Рассмотрим два вида моделей однослойной цилиндрической катушки по рис. 1.7, а и 1.8, а. На рисунках приняты обозначения: dn-диаметр провода;

Рис. 1.7. Геометрическая модель цилиндрической катушки (первый

а - представление обмотки совокупностью плоских витков; б - представление каждого витка двумя контурами: контуром It по оси проводника и контуром k по следу витка на каркасе

Лз-.шаг иамотки; ? -длина катушки; Гг-радиус каркаса; Г1 = Г2-1--fdny2 -средний радиус витка. В модели по рис. 1.7, а витки обмотки заменены плоскими витками. Модель по рис. 1.8, а соответствует реальному расположению обмотки. Эта обмотка не замкнута, и рассчитать ее индуктивность нельзя, так как теряет смысл ее собственное потокосцепление (1.14). Поэтому сравнение двух моделей возможно только при 1-сх> или / 2г1. В этом случае можно считать электромагнитные состояния всех витков в пределах каждой модели одинаковыми, а потокосцепление с каждым из них практически равным потокосцеплению с витком Ч'в, расположенным в середине катушки.

Для оценки Wb представим каждый плоский виток в модели катушки по рис, 1,7, а двумя круговыми контурами (рис, 1.7,6): контуром h с радиусом 7-1 (по оси витка) и контуром k с радиусом Гг (по следу витка на каркасе). Магнитное поле катушки приближенно определяется током i контуров U всех витков, а потокосцепление каждого витка - совокупностью магнитных линий, охваченных контуром 2. Воспользовавшись (1.9) и преобразованиями, аналогичными

§ 1.5

Влияние шага намотки катушек

примеру 1.2, найдем

Wf2 Л

ixj (>0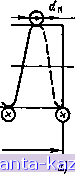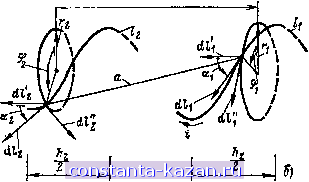

(1.26)

Рис. 1.8. Геометрическая модель цилиндрической катушки (второй

о - расположение обмотки; б - представление обмотки двумя контурами: контуром Л по оси проводника и контуром /а по следу обмотки на каркасе