быть применен лишь при ряде ограничений. Действительно, при наличии экрана магнитный поток в сердечнике с зазором замыкается только между неэкранированиыми торцами. При отсутствии экрана пути прохождения магнитного потока через воздушный зазор существенно усложняются, приобретая объемный характер. Для того чтобы магнитный поток в таком сердечнике замыкался в основном между торцам:;, необходима высокая относительная магнитная проницаемость матер:1ала, либо достаточно малая длина воздушного зазора. При отсутствии этих условий необходим расчет полной схемы замещения катушки с сердечником по методу, описанному в § 4.2, с учетом конкретных особенностей конструкции сердечника.

4.5. КАТУШКИ ИНДУКТИВНОСТИ С ЗАМКНУТЫМ СЕРДЕЧНИКОМ

Замкнутый сердечник позволяет максимально использовать магнитные свойства материала, из которых он изготовлен. Так как магнитные свойства материала проявляются весьма разнообразным образом и зависят от многих причин, то для количественного расчета значений индуктивностей необходимо принять определенные допущения. Ниже рассмотрены способы учета влияния формы сердечника и магнитного гистерезиса на -параметры катушки в режиме намагничивания синусоидальным током.

Рис. 4.15. Кольцевой сер- ФоР^ сердечника

дечник индуктивность катушек

Рассмотрим кольцевой сердечник (рис. 4.15) из материала с Цг = const и ничтожно малыми потерями, На сердечнике равномерно распределена обмотка ш с током (. Напряженность поля в любой точке такого сердечника, находящейся на расстоянии гот оси его симметрии, одинакова и равна

Я=(ш)/2яг = В/ДгР-о-Магнитный поток в сердечнике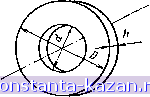

Ф = п \ Bdr ---In - ,

,1 2л d

где d и D - внутренний и внешний диаметры; h - высота сердечника.

Индуктивность катушки без учета индуктивности рассеяния аФ 1ц 11 D

2я d

Ограничившись двумя членами разложения в ряд Тейлора вели-

§ 4.5 Kari/wKM индуктивности с замкнутым сердечником

чины 1л-

D D-d

для тонкостенного кольцевого сердечинка при

d D

d-D, площади поперечного сечения Sc=h{D-d)l2 и длине средней линии /cp=nD, получим

Еслн выражение для ннду!(Т!;вности перешшать в виде

Иг 10

Did - 1

ln(D/a!) , .=0

cp - i icp

где /ср = я{/Э-d) - длина средней линии сердечника, то можно оценить влияние формы сердечника коэффициентом формы, который в общем случае для магнитопровода с прямоугольным сечсннем является функцией отношения внешнего и внутреннего периметров Пвн и Пвт:

* Пв /Пз,-1 2

4.5.2. Влияние магнитного гистерезиса на индуктивность KaryuieK

На ркс. 4.16 сплошной линией показана экспериментально снятая статическая петля гистерезиса сердечника, представляющая собой зависимость среднего (но сечению) значения индукции В = Ф/5о от напряженности магнитного поля на средней линии =да ср, где Sc - площадь поперечного сечения и /ср -длина средней линии сер-

В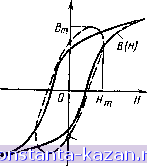

Вт sin(-3n)

Рис. 4.16. Замена петли гистерезиса эквивалентным эллипсом

Рис. 4.17. Катушка с сердечником в цепи переменного тока:

о -схема цепи; б ~ последовательная электрическая модель; в - параллельная электрическая модель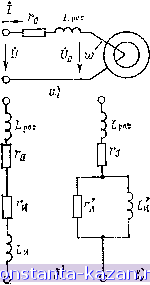

дечника. При этом автоматически учитывается форма сердечника.

Полное потокосцепление с обмоткой катушки состоит из потокосцепления рассеяния, и потокосцепления намагничивания. Учитывая это обстоятельство, реальную катушку можно представить в виде последовательного соединения индуктивности рассеяния Lpac, активного сопротивления обмотки го и так называемой идеализированной катушки (рис. 4.17, а). Свойства идеализированной катушки зависят только от магнитных свойств сердечника и числа витков обмотки {7}. Для анализа процессов в идеализированной катушке статическую петлю гистерезиса сердечника можно заменить эквивалентным эллипсом. Обычно площадь перекрытия эквивалентного эллипса и статической петли гистерезиса должна составлять 80-9(1 % площади каждого из них в отдельности.

При одинаковом направлении обхода статической нетлн гистерезиса и эквивалентного ей эллипса (см. рис. 4.16) уравнение последнего Б параметрнческсй форме можно записать в виде (/) = Я^з1псоЛ I

B(/)=B, sin((D/-6 ), J

где Вт и Н„1 - максимальные значения индукции и напряженности магнитного ноля; бц - угол потерь энергии в сердечнике.

Так как индукция и напряженность магнитного поля изменяются но синусоидальному закону, то для расчета катушки можно воспользоваться комплексным методом. Комплексное сопротивление идеализированной катушки

и /с^одФ jawsB S в

*с Вт .с т о *с Вт с . . т ,. . г.,

= (сю2--- smf>n + j(ow-;--r-cos бп = л„-f/(oL , (4.15)

cp- m cp m

где Ли И (oL - активное и индуктивное сопротивления идеализированной катушки.

Полная эквивалентная схема замещения катушки в соответствии с (4.15) приведена на рис. 4.17,6. На рис. 4.17, е приведена другая часто встречающаяся разновидность этой схемы, в которой

г, = coiL -

Наличие резистивного элемента в схемах замещения определяется потерей энергии в сердечнике на магнитный гистерезис.

Использование для расчета катушек экспериментально определенной динамической нетлн гистерезиса сердечника учитывает влияние как формы сердечника, так и всех его электромагнитных свойств: магнитного гистерезиса, магнитной вязкости и электропроводности.

4.6. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ КАТУШЕК ИНДУКТИВНОСТИ

Будем называть собственные и взаимные индуктивности катушек индуктивными параметрами последних, а совокупность опреде-