и воздушного зазора

<> Мо %(л)

Зп(л) - СзБ'

С3п(л)--о~ + зв - -9

где Сзя(л)-ширина правого (левого) участков нахлеста, если смещение частей А и Б составного сердечника в направлении, перпендикулярном плоскости симметрии yz, равно ±0:

( C5b/2±0>Cs/2; Зп(л, = + <зи - Т 9, если с,/2 + ± Э > с,/2 +

С55/2±9>С5/2; , C5s/2 -f ± 9 < Сд/2 + сз5 С5в/2±9< С5/2; если C5g/2-f ±е<

I С5в/2±0<С5/2; Зп(л)-сзл. если2 д^2

После последовательного преобразования элементарных треугольников магнитных сопротивлений в эквивалентные звезды и суммирования слагаемых получим магнитное сопротивление правого (левого) участка нахлеста.

Полная магнитная проводимость составного сердечника но схеме замещения на рис. 4.18, б равна

Sm,cA m,cS

м,сЛ 8м,сБ Sta,cB (м,нах,п м,нак,л)

= /(С1Л. 15.....5И- 5S- п' л- Мм Mrs, 9).

(4.20)

Примем, что значения всех внутренних параметров составного сердечника a:i = Cia, Х2=С2а,... являются независимыми случайными величинами;

случайные значения всех внутренних параметров подчиняются нормальному закону распределения с математическим ожиданием по (4.17) и среднеквадратическим отклонением по (4.18);

случайные значения всех внутренних параметров после отбраковки изготовленных изделий находятся в пределах своих допусков

Это позволяет выбрать совокупности предельных значений внутренних параметров, при которых магнитная проводимость достигает минимального gumin и максимального gumax значений, т. е. реализовать метод наихудшего случая (см. пример 4.2).

Из центральной предельной теоремы [5] следует, что закон распределения магнитной проводимости составного сердечника близок

к нормальному с математическим ожиданием

Л

М IgM] =

и среднеквадратическим отклонением

1ём] = z-Г 71 ёмк

1\ *=1

N - 1

(4.21)

(4.:2)

где Л' - достаточно большое (обычно не менее 50-100) число расчетов модели по (4.20) при случайных значениях внутренних параметров xi в заданных пределах допусков ДХ(.

Разделим диапазон изменения магнитной проводимости

на П= {g max-g mm)/AeM рЗВ-

ных интервалов. Если из общего числа испытанпй модели в AN случаях значения g находятся в одном из интервалов 1<т<п, то средняя плотность вероятпостп этих событий

,cp)m-

(AN)/NAg. (4.23)

Совокупность значений Р(8и,<:р)т для всего дианазонэ изменения магнитной проводимости определяет гистограмму распределения плотности вероятности, переходящую в закон распределения р(й^м) приЛ->оо и,Д§м->0.

На рис. 4.19 приведена структурная схема расчета статистических характеристик магнитной проводимости составного сердечника на ЭВМ. Числовые значения статистических характеристик a[Xi] и

допусков Axi для всех внутренних параметров х,-, а также число испытаний являются исходными данными.

Для выработки случайных значений всех внутренних на-

С

Нача/10

BSod даннш 7

c = k==1

Датчик случайных чисел 4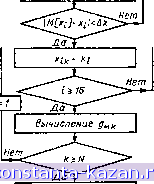

Вычисление M[gJ,6[gJ,p(y ,cp)m

/ 8:iM~ 7

/ результатов / С Коней,

Рис. 4.19. Структурная схема программы расчета статистических характеристик составного сердечника

раметров х, при k-м испытании модели используется программный датчик с-!учайиых чисел с нормированным нормальным законом распределения и плотностью вероятности

Р (I) =----~ е- \ (4.24)

Нормированный нормальный закон распределения р() получается нз ненормированного нормального закона распределения внутренних параметров с плотностью вероятности

Р (Xi) =-e-Wi]-i)y Vi] (4.25)

о [Xi] V2n

умножением последнего па o{xi] и заменой переменных

Xi==M[Xi]-lo[xi]. (4.26)

Выражение (4.26) позволяет вычислить случайное значение внутреннего параметра Xi, если программный датчик выработал случайное число . Совокупность случайных значений всех внутренних параметров, находящихся в пределах допусков, используется для й-го испытания модели, т. е. для вычисления gmk.

Метод статистических испытаний позволяет также оценить чувствительность магнитной проводимости составного сердечника к изменению того или иного его внутреннего параметра Xi. Для этого при испытании модели составного сердечника по (4.20) N раз и последующем вычислении математического ожидания магнитной проводимости щця] по (4.21) все внутренние параметры принимают случайные значения в пределах своих допусков A.v за исключением одного, имеющего постоянное значение.

Если в каждой серии из Л' испытаний выбранному внутреннему параметру задавать новое фиксированное значение, то зависимость

M[g,]=f(Xi) (4.27)

- определяет линию регрессии. Линия регрессии показывает, как в среднем зависит значение магнитной проводимости от значения того или иного внутреннего параметра Xi. Так как модель составного сердечника содержит две одинаковые части, то линии регрессии от одноименных параметров частей совпадают.

Числовые статистические характеристики M{gw\ и a[gn] магнитной проводимости сердечника однозначно определяют одноименные числовые статкстические характеристики (4.5) индуктивности катушки

M[Lu\ = wM{g]\ a[LHaMl = ?a[5M]. (4.28)

где w - число витков обмотки.

Пример 4.5. Числовые статистические характеристики и допуски случайных значений взаимно независимых внутренних параметров