Результирующая матрица передачи структуры (см. рис. 2.19) рассчитывается как обычно: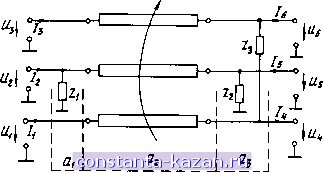

Рис. 2.19. Управляемая структура на трехпроводных связанных полосковых линиях

а = П а,.

От матрицы а для расчета рабочих параметров управляемых устройств необходимо перейти к матрице производного четырехполюсника а, используя следующие граничные условия на входных и выходных зажимах двенадцатиполюсника с матрицей а:

/2 = О, /4 = /5 = /б = 0. (2.4.3)

После перемножения матриц и перехода к а получаем аи = S-TG-Q (R-G-MQ);

ax2 = T{R-G-MQ)-; (2.4.4)

аг, =D-G- - {F~D-G-M){R-GMQ)-G-Q a22 = {F-DG-M) {R~G-MQ)-\

где

D = U42-041052/051; F = 043-04,053/051; G = 062-061052/051;

M = 063 - 061053/051;

Q = 032-031052/051; R = 033-031053/051; 5 = ai2G~-G~aiia52/a5i; T = aiia52G~M/a5i-aiia53/a5i+ai2G~ - - a,2G-iW + 0,3.

Итак, задаваясь конкретными типами регулирующих элементов с сопротивлениями Z, Z2 и первичными параметрами трехпроводной СПЛ, с помощью приведенных формул рассчитываем параметры структуры на рис. 2.19.

глава 3

УПРАВЛЯЕМЫЕ СЕКЦИИ НА ДВУХПРОВОДНЫХ СВЯЗАННЫХ ЛИНИЯХ

Функциональные возможности управляемых структур на основе МСПЛ с неуравновешенной связью были впервые исследованы на примере управляемых секций в работах [59, 20, 35]. Управляемые секции (УС) находят применение в качестве звеньев для построения фазовращателей [19], возможно также использование их как отрезков линии с изменяющимся волновым сопротивлением, ячеек режекторных фильтров [35, 60].

Анализ характеристик УС основывается на приведенных в гл. 2 соотношениях. В качестве первичных параметров нами брались матрицы погонных сопротивлений Z и проводимостей Y, длина связанных линий / и величины нагрузочных сопротивлений Zi [20]. Расчет матриц Z, Y проводится тем или иным методом по размерам поперечного сечения СПЛ, которые на первом этапе синтеза (проектирования) неизвестны. Поэтому при проектировании устройств на основе УС появляется задача сравнить разнообразные конструктивные варианты, исходя нз критерия предельно достижимой регулировки параметров через систему обобщенных параметров. Очевидно, что решение подобной задачи можно рассматривать как один нз этапов структурного синтеза.

3.1. Предельно достижимая регулировка параметров для структурных схем, содержащих один источник возбуждения

Рассмотрим схему секций, показанную на рис. 3.1. Как уже отмечалось, будем считать, что в связанных линиях распро-

Рис. 3.1. Управлиемая секция с одним источником возбуждения

страняются квази-Т волны, которые можно описать так, как

это сделано в работе [20]. Напряжение падающей волны в линии с номером / запишется

[/,р {х) = Л,ехр/ ((o/-p,x-f фО + Aiexpi (со-М+фг), (3-1.1)

где Ли у42 - модули комплексных амплитуд напряжений быстрой и медленной волн; фь ф2-фазовые сдвиги, определяемые как arg(v4i) и arg (/42) соответственно; Эь Эг - собственные фазовые постоянные для быстрой н медленной волн.

Фаза падающей волны напряжения U\p отыскивается по формуле

argUip = arctg {JmUip/ReUip), (3.1.2)

а фазовая скорость

(3.1.3)

Сложность вычисления Уф связана с нахождением амплитуд А\, Ач, фазовых сдвигов фь ф2, как функций от величин регулирующих сопротивлений Z2 и г\, при этом вся система первичных параметров, т. е. Pi,2 матрицы Z, Y и длина / СПЛ, будет также определять характер и диапазон изменения Уф. Эти затруднения значительно снимаются, если ввести систему обобщенных параметров в следующем виде [115]:

d = Л,/Л2;

(3.1.4)

n = p2/Pi;

- (Э2 -ЭО-+ф! -ф2-

(3.1.5) (3.1.6)

Физический смысл обобщенных параметров достаточно очевиден: d характеризует отношение амплитуд быстрой и медленной волн, являющихся составляющими падающей волны в первой линии; п отражает степень неуравновешенности электромагнитной связи связанных полосковых линий; \з - фаза интерференционного множителя.

Подставив в формулу (3.1.3) соответствующие величины, входящие в (3.1.1), (3.1.2), после преобразований получим выражение для вычисления Уф через обобщенные параметры (3.1.4) - (3.1.6):

(3.1.7)

Пределы изменения согласно формуле (3.1.7) зависят от того, какие границы регулировки параметра d обеспечиваются в исследуемой структуре. Приведем в качестве примера расчет обобщенных параметров в секции СПЛ, имеющей такие матрицы емкостей и индуктивностей:

2,0599-10 1,6250-10 1,6250-10 1,6250-10

, пФ/м

2,1544 О

О

0,2154

, мкГн/м.

Регулирующие элементы - емкости, включенные в плечах 2,4 длина СИЛ /=0,05 м. СПЛ реализуются в виде меандровой линии, перекрытой управляющей полоской [20].

Расчет на ЭВМ дал следующие значения обобщенных параметров при емкости регулирующих элементов Ср= 0,01 пФ:

d = 1,3210223; п =8,2379212; \з = 1,3290209, рад, а при Ср= 200 пФ:

d = 0.32380652;

п = 8.2379212;

= 1,3204576, рад.

Из сравнения численных данных можно сделать вывод, что вариация 22=24 = (/соСр) приводит в основном к изменению d. Параметр п для фиксированной структуры поперечного сечения СПЛ остается неизменным, г|з меняется незначительно. Следовательно, механизм регулирования в терминах

обобщенных параметров объясняется изменением d, т. е. отношения модулей амплитуд нормальных составляющих волн, распространяющихся в связанных полосковых линиях с неуравновешенной электромагнитной связью. Данное обстоятельство подтверждает правильность основного результата работы [20], в которой подобного доказательства не приводилось.

Из сказанного можно также сделать весьма важный вывод о том, что исследование физической реализуемости (3.1.7) следует связать с оценкой пределов изменения d в зависимости от 22 и 24. Аналитическая зависимость d (22, 24), полученная в сравнительно простой форме, открыла бы путь к синтезу устройств рассматриваемого типа по основному параметру: регулированию (или фазового сдвига). Однако, как это видно из анализа квази-Т волн в управляемых секциях на СПЛ [20], решение такой задачи возможно только на ЭВМ. Тем не менее, как будет показано ниже, возможна оценка пределов регулировки Уф и построения достаточно общих зависимостей Уф от d при разных ijj.

Для схемы на рис. 3.1, содержащей единственный источник возбуждения, параметр d зависит от Z2 следующим образом:

ко -\- K20Z2

(3.1.8)

где коэффициенты ke, ko и волновые проводимости Y2e, У20

определяются из работы [20].

Зная пределы изменения d, можно воспользоваться графиком зависимости Уф или формулой (3.1.7), чтобы рассчитать регулировку у . Абсолютные значения угловой частоты со и собственной фазовой постоянной Pi, как это видно из выражения (3.1.7), не влияют на регулировку Уф, понимаемую как отношение максимальной величины Уф к минимальной, поэтому целесообразно рассчитывать параметр V=vi/<a. Серия кривых, отражающих эту зависимость, приведена на рис. 3.2. Как видно из графиков, при возрастании d от О до с V изменяется от п до 1, если г|з<0,5. Эти пределы изменения V соответствуют фазовым скоростям быстрой (верхняя граница) и медленной волн (нижняя граница). Выход за отмеченные пределы,