Физические свойства многосвязных полосковых структур*

Уравновешенная злектроматитная Чвяз^

Структуры со славы-ми трекрестиыми связями

Неуравновешенная

злекпцюмгнитная связь

Структуры с сильными перекрестными ШШИ

*) Примечание. В прямоугольниках показано соответствие конструктивным признакам.

Рнс. 1.1. Классификация миогосвязных полосковых структур по конструктивным признакам и физическим свойствам

лее важных физических свойства: уравновешенность или неуравновешенность электромагнитной связи полосок [11]; наличие или отсутствие так называемых перекрёстных связей [12].

Первое свойство зависит от степени заполненности диэлектриком в поперечном сечении структуры (рис. 1.2). Показанная конструкция, очевидно, характеризуется как система с неуравновешенной электромагнитной связью, т. е. такая.

Рис. 1.2. Связанные полосковые линии с плшарным расположением полосок на диэлектрической подложке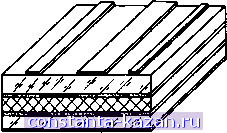

Рнс. 1.3. Многопроводная полосковая структура с объемным расположением полосок в слоистом диэлектрике

для которой коэффициенты связи индуктивные и емкостные fee не равны (тождественно по смыслу неравенство коэффициентов связи по напряжению и току К, [И]). В практически применяемых конструкциях, пожалуй, лишь хорошо известные симметричные связанные полосковые линии с однородным диэлектриком и наличием замкнутого экрана представляют собой систему проводников с уравновешенной электромагнитной связью. Отсюда класс структур с неуравновешенной связью более широк.

Определение второго из названных свойств (см. рис. 1.2) проводится путем сравнения коэффициентов связи несоседних проводников с коэффициентами связи рядом расположенных полосок. Планарное расположение полосок на подложке дает возможность пренебречь перекрестными связями [12].

Многопроводная полосковая структура с объемным расположением полосок в неоднородном диэлектрике (см. рис. 1.3)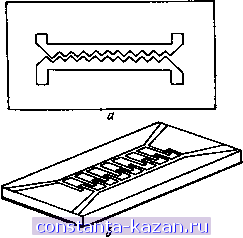

Рнс. 1.4. Связанные полосковые лнннн с компенсацией неуравновешенности электромагнитной связн

характеризуется сильными перекрестными связями. Как и структура с планарным расположением полосок, подобная конструкция МСПЛ содержит связанные проводники с одинаковой физической длиной в области электромагнитной связи. В силу неоднородности диэлектрика МСПЛ (рис. 1.2, 1.3), как уже отмечалось, обладают свойством неуравновешенности связи по электрическому и магнитному полям. Часто данное свойство является нежелательным при создании направленных ответвителей и других устройств [13, 109-111]. Стремление добиться одинаковости фазовых скоростей нормальных волн привело к созданию двухпроводных СПЛ (рис. 1.4) с фактически неодинаковой физической длиной в области связи [14-18, 111]. Иная цель преследовалась при создании структуры МСПЛ, изображенной на рис. 1.5. За счет большой разницы физических длин в конструкции достигается существенная неуравновешенность связи, что позволяет добиться расширения функциональных возможностей устройств на базе подобных МСПЛ [18, 19].

Строго говоря, в связанных полосковых линиях распространяются волны, имеющие сложную структуру с продольными £ и Я составляющими [4]. Классификация волн, исходя из анализа условий их существования, представляет собой мало изученную проблему даже в отношении простых конструкций

Рнс. 1.5. Многосвязная полосковая структура, содержащая связанные лнннн с сильно неуравновешенной связью

одиночных полосковых линий, не говоря уже о связанных структурах [6, 13]. Поэтому при моделировании МСПЛ чаще всего исходят из концепции существования так называемых квази-Т волн [13]. Есть несколько причин, по которым роль теории МСПЛ на основе квази-Т приближения не только не уменьшается, но и несколько возрастает в противовес существовавшему мнению о неприменимости подобного подхода. Во-первых, в настоящее время не существует альтернативных решений, предоставляющих разработчикам СВЧ узлов более эффективный матричный аппарат анализа МСПЛ. Во-вторых, концепция нормальных волн как естественное расширение понятия квази-Т волна применима не только для анализа МСПЛ и других структур с почти поперечными волнами, но и структур с более сложной конфигурацией электромагнитного поля путем увеличения связности и построения более сложной эквивалентной схемы [21-26, 29].

Модели многопроводных связанных полосковых линий, по существу, представляют собой эквивалентные цепочечные схемы отрезков МСПЛ. Пример одной из наиболее общих моделей приведен на рис. 1.6. Поясним обозначения элементов эквивалентной схемы: Lu - собственные и взаимные индуктивности проводников структуры; Cis - собственные и взаимные емкости; 7? - последовательные сопротивления проводников структуры; Gis - собственные и взаимные проводимости; i,s= 1, 2, л, где л - количество проводников МСПЛ.

В зависимости от способа задания параметров на бесконечно малом участке длины dx или на отрезке конечной длины Адг эквивалентная схема МСПЛ дает возможность получить дифференциальные или конечно-разностные уравнения для описания волнового процесса. Соответственно параметры модели Lis. Cis, Ris, Gis приобретают смысл погонных или квазисосредоточенных параметров.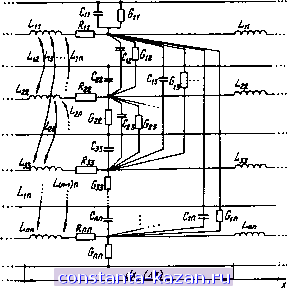

Рнс. 1.6. Эквивалентная схема многопроводных связанных полосковых линий

Систему первичных погонных параметров МСПЛ удобно представить в виде матриц L, С, R, G, составленных из L,s, C,s, Ri Gis. Для регулярных МСПЛ L, .... G не зависят от координаты X, вдоль которой распространяются квази-Т волны.

Матрицы L, С - вещественные,квадратные,размером пХп. Элементы этих матриц имеют смысл индуктивных и емкостных коэффициентов. Кроме того, L и С обладают свойством симметрии. Матрицы записываются следующим образом:

Lll Li2 Li3 ... L\

Li2 L22 L23 -.. i2n

Li3 L23 L Lin Lin L

Cw -C12

- C12 22

- Ci3 -23

-C,3

-C23 C33

-C2n -Сзп

-Cln -Cin -Сзп

Матрица R - диагональная, матрица G - квадратная симметрическая. Из-за скин-эффекта и зависимости потерь в диэлектриках от частоты элементы матриц R и G также зависят от частоты.

От матриц погонных индуктивностей, емкостей, сопротивлений и проводимостей можно перейти к более общим параметрам - комплексным сопротивлениям и проводимостям Zis = Ris-\-j(aLis, Yis = Gis-\-joiCis и соответствующим матрицам

Z = R -Ь /(oL, Y = G -Ь /(оС.

Эквивалентная схема (см. рис. 1.6) уже при малых значениях элементов Ru, G,s дает возможность учитывать дисперсию в полосковой структуре, т. к. сопротивления и проводимости вместе с Lis. Cis дают частотную зависимость элементов матриц Z, Y.

Двухпроводная полосковая структура, на основе которой конструируется большое число разнообразных по функциональному назначению устройств, имеет эквивалентную схему приведенную на рис. 1.7.

П22 T У ЫНгг

Рис. 1.7. Эквивалентная схема двухпроводных (трехсвязных) полосковых линий

Построение эквивалентной схемы МСПЛ так или иначе основывается на анализе электромагнитного поля структуры. В этой связи следует отметить, что эквивалентная схема типа изображенной на рис. 1.6 может учитывать существование не только квази-Т волн, но и волн высших типов [21, 22, 26]. Так, на рис. 1.8 приведена эквивалентная схема дисперги-