Рис. 1.8. Эквивалентная схема полосковой лнннн, составленнан с учетом дисперснн путем повышения порядка связности

рующей микрополосковой линии, в которой распространяются квази-Т и квази-ТЕю волны. Существование волн высших типов отражено соответствующими элементами схемы (рис. 1.8) и повышением порядка связности рассматриваемой системы. На эквивалентной схеме ео, цо, Цо - проницаемости и характеристическое сопротивление свободного пространства; е Zo - эффективная статическая диэлектрическая проницаемость и характеристический импеданс при воздушном заполнении; К - волновое число частоты среза для не связанной ТЕ-моды; Ci2 = ktt - емкость связи (fe - коэффициент емкостной связи, О < А < 1).

1.2. Матричные телеграфные уравнения

Телеграфные уравнения обобщенной регулярной МСПЛ могут быть получены разными путями (краткая историческая справка по данному вопросу приведена в работе М. X. Захар-Иткина [27]). Они выводятся из уравнений Максвелла [28- 30, 107], записываются как следствие теоремы взаимности электротехнических цепей [27] или получаются из законов Кирхгофа предельным переходом от уравнений цепи с сосредоточенными параметрами к уравнениям для структуры с распределенными параметрами. Подробный вывод телеграфных уравнений для двухпроводных СПЛ без учета потерь дан в работах [2, 75].

Рассмотрим отрезок МСПЛ длиной dx с эквивалентной схемой (см. рнс. 1.6). Обозначим напряжения и токи так, как

Uf(K*dx)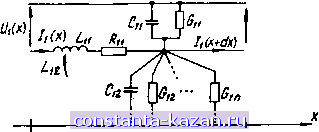

Рис. 1.9. К выводу телеграфных уравнений

ЭТО показано на рис. 1.9. Придадим параметрам эквивалентной схемы смысл погонных параметров. Тогда справедливы следующие уравнения:

f/. {x+dx) - t/. {X) -LudxJM- L dx-

L, dx- Rudxhix);

U. (x+dx) - и2 (jc) = - Ltidx

dh {X) dt

U.dx--,

(1.2.1)

-Undx-R22dxh{x)-

(1.2.2)

Un (jc+djc) - Un {x) = - Undx

jx) dt

- Lindx

dhjx) dt

-L dx- R ndxfn{x);

dt dU,{x)

/, {X + dx) - /, {X) -Cudx - + Cndx +,..., +

+ Ctndx- Gudx Uix)+

+ Gx Uix) +,..., +Gtndx U {x);

(1.2.4)

h (x+dx) - h (x) = C dx - Ых +.....+

(1.2.3)

+ C2ndx + G,2 dx U,{x) ~ G22 dx U2 (x) +,...,+

+ Gindx Unix); (i.2.5)

/ (x+dx) - In (x) = Cindx+ C2ndx-

- Cnndx + Gtndx Ut (x) + G2ndx U2 {x) -

-GnndxUnix). (1.2.6)

Переходя к системе первичных параметров в виде матриц L, С, R, G и осуществляя деление на dx левой и правой частей уравнений (1.2.1) - (1.2.6), получим

£(l) = -L(I)-R(I); £() = -C(U)-G(U),

41.2.7) (1.2.8)

где (II), (I) - столбцовые матрицы напряжений и токов в линиях.

В силу регулярности МСПЛ и отсутствия в рассматриваемых конструкциях локальных неоднородностей очевидным образом функции Ui (х), Ii (х) - непрерывно дифференцируемые. На этом основании будем считать, что

£(U) = -lA((,)) r((,)). (1.2.9)

и путем подстановки в (1.2.9) выражения (1.2.8) получим

}(U).

(1.2.10)

(U) = Lcg (U) + (LG+RC) S- (U) + RG (U).

Аналогичное уравнение имеем для токов

(I) = CLi; (I) -Ь (GL-bCR)l (I) + GR (I).

(1.2.11)

Телеграфные уравнения (1.2.7) - (1.2.11) дают возможность исследовать волновой процесс в МСПЛ в переходном режиме при воздействии на них сложных сигналов. При гармоническом возбуждении МСПЛ, что чаще всего имеет место на практике, уравнения упрощаются. Примем зависимость от времени напряжений и токов 16

и {x,t) -- и (х) ei-\ I (jc,0 = I (jc) ei . Тогда уравнения (1.2.7), (1.2.8) перепишутся

(U) = -ZI; (1.2.12)

= -YU, (1.2.13)

где Z = R--/(i)L, Y = G--/(uC - соответственно матрицы сопротивлений и проводимостей.

Последняя форма уравнений используется в большинстве работ, где рассматриваются многопроводные структуры [25, 28, 29]. Непосредственно из (1.2.12), (1.2.13) или из (1.2.10) и (1.2.11) получаем еще одну форму телеграфных уравнений

(U) = (ZY) U; (I) = (YZ) I.

(1.2.14) (1.2.15)

1.3. Волновые свойства МСПЛ и решение телеграфных

уравнений

В работах, посвященных теории связанных линий, можно найти различные подходы к решению телеграфных уравнений [11, 13, 23, 27-34]. Несмотря на некоторое разнообразие математических методов, все решения основываются на представлении полной картины волновых процессов в МСПЛ в виде суперпозиции нормальных волн [27].

Решение телеграфных уравнений (1.2.14) и (1.2.15) ищется в виде

U = Ae 1 = 81 (1.3.1)

После подстановки (1.3.1) в исходные уравнения (1.2.14) и (1.2.15) получаем систему относительно напряжений в линиях

(ZY-y£)A = 0, (1.3.2)

нетривиальное решение которой возможно при условии

ZY-y£=0, (1.3.3)

где Е - единичная матрица.

Аналогично для токов (YZ - у'Е) В = О- (13 4)

2 Заказ 0376 17

YZ -у'Е\ = 0.

(1.3.5)

Характеристический многочлен матрицы а = ZY имеет степень п, поэтому в общем случае существует п отличающихся по абсолютной величине! собственных чисел матрицы а, т. е. 2п значений у.

Предположим, что амплитуда напряжения в первой линии Al для любой из у, известна (s = 1, 2, п). Тогда остальные амплитуды сможем найти из неоднородной системы уравнений

(а^ - у^Е)Аг = -аЛ

(1.3.6)

где

Без нарушения степени общности можно для любой у?взять Л1=1. Тогда

А, = -(а, - у'Е)-

,(1.3.7)

Точно так же нз (1.3.4) устанавливается связь между амплитудами токов Б линиях

В,= -(а?-у2£)-

(1.3.8)

где т - знак транспонирования.

Из телеграфных уравнений вида (1.2.12), (1.2.13), кроме того, устанавливаем связь между В и А:

В=-УА7-. (1.3.9)

Очевидно, что каждая столбцовая матрица А и В, найденная для какого-либо коэффициента распространения у^ путем решения уравнений (1.3.7), (1.3.8), будет представлять собой собственный вектор; нахождение всех векторов даст матрицу собственных векторов напряжений А^, и токов А,. Поскольку мы, по существу, выполнили нормирование амплитуд напряжений и токов относительно Ль fii,назовем А^, А, матрицами нормированных амплитуд. Они имеют следующую структуру:

(1.3.10)

А, = -

Yn Yi2 ... Km

/П21 Y\\ Ш22 112 2/1 Ill

Шпх Y\\ nini Y\2 ... ni Yn

(1.3.11)

Коэффициенты кц, шц {i = 2, 3.....n; / = 1, 2, 3, .... n) находятся

из (1.3.7) и (1.3.8) как соответствующие элементы матриц Ар и Вг с учетом их связи, вытекающей из уравнения (1.3.9).

Исходя из (1.3.1) и физического смысла у, отрицательные значения у соответствуют падающим волнам, а положительные V - отраженным. Обозначим соответствующие собственные векторы \~ Ajt Ar(-f для падающих волн). Подстановкой решения (1.3.1) в уравнения (1.2.12), (1.2.13) убеждаемся, что

Ац = Aj= \и\ А, = А|.

Полная матрица собственных векторов A (матрица нормированных амплитуд) запишется

. lA А„ (1.3.12)

А, А,

В силу (1.3.9) полезна еще одна формула для А,:

А, = -УАиу-. (1.3.13)

В общем случае элементы матрицы Ащ и - комплексные числа. Матрицы у и а подобны. Блоки матрицы А„, являющиеся собственными векторами напряжений н токов падающих и отраженных волн, трансформируют а илн к у^, следовательно, а - матрица простой структуры илн диагонилизн-руемая матрица [41]. Последнее обстоятельство имеет в отношении многосвязных полосковых структур очевидную физическую интерпретацию в виде существования в МСПЛ квази-Т волн с коэффициентами распространения yi, уг, Уп- Практически всегда, если в МСПЛ учитываются все возможные связн между полосками и потерн, отсутствует кратность собственных значений у? матрицы . Волны, имеющие коэффициенты распространения yi, уг..... Уп, представляют собой, по

существу, собственные квази-Т волны, физическая природа которых объясняется общей теорией электромагнитных волн [30, 31]. Факт существования в полосковых структурах волн