с отличающимися у подтвержден экспериментально [42], а зависимость у от режима возбуждения линий используется в практике построения управляемых устройств [19, 20].

Запишем теперь общее решение телеграфных уравнений, позволяющее найти напряжения и токи в сечении х, если известны напряжения и токи в точке ж=0:

V{x) Цх)

U(0) 1(0)

(1.3.14)

Решение (1.3.14) дает детальную картину волновых процессов в МСПЛ, которая очевидным образом зависит от граничных условий. С помощью (1.3.14) можно исследовать как собственные колебания, т. е. нормальные волны, так и связанные волны напряжений, токов [20 .

1.4. Матричные параметры отрезков л-проводных связанных линий

Расчету классических и волновых матриц л-проводных связанных линий посвящены, например, работы [42-47]. Рассмотрим наиболее общий случай определения матричных параметров МСПЛ с потерями, т. е. когда элементы /? и Gis матриц R и G сравнимы с элементами (oL,s, (oC,s матриц L и G, умноженных на частоту со. Обозначим напряжения и токи на входе отрезка л-проводной линии согласно рис. 1.10. Выходные напряжения и ток.ч определяются через входные следующим образом:

U(/)

!(/)

Определим по формуле Фробениуса [41]

(1.4.11

А- -

--2

(1.4.2)

Подставив (1.4.2) в (1.4.1) и изменив направление токов на входе и выходе 2л-полюсника на общепринятое, получим матрицу а:

(1.4.3)

2п-поя1всмик

Г

Рис. 1.10. Отрезок связанных полосковых линий как 2/1-полюсник

Между собственными векторами A и А, существует связь д = YAuy , которая дает возможность преобразовать выражение (1.4.3) к следующему виду:

A.chy/A-

-YA 7-sh7/A-

-А

-iv-i

(1.4.4)

где т - знак транспонирования.

Вычисление матриц у, z н волновых матриц s, t может быть проведено через известную связь между ними [2, 63]. Возможен н другой путь - получить матрицы непосредственно нз решения телеграфных уравнений.

Предположим, что мы нашли каким-либо образом амплитуды напряжений падающих и отраженных волн в линиях Up и Ur. Тогда сможем записать

U(x) = A Up.-v + A,U.. (,4 5

I (JC) = - Wy-U.ey + YA v-U.e

В последнем уравнении системы (1.4.5) произведение YAy7~ по физическому смыслу соответствует волновой проводимости линии для определенного типа волны с коэффициентами распространения 7s. Обозначим Y = - YAy . Тогда матрица-столбец токов в линиях примет вид

I (JC) = \r,Vpe- - YmVre . (1.4.6)

Для напряжений и токов из граничных условий имеем [64]:

U(0) = A U,--A U.; и (/) = А„и^- + 1(0) = Y Up- Y U,;

I (/) = Y Upe- - Y Vre . (1.4.7)

Переходя к матричной записи (1.4.7) и используя классическое определение матрицы проводимостей у, получаем матричное уравнение для ее нахо;<дения

(1.4.8)

откуда сразу же следует, что

После несложных преобразований имеем

(1.4.10)

При вычислении волновой матрицы примем граничные условия (рис. 1.11):

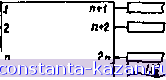-КО) I(t)-

II

U(0)

1 Mi.

-0 0

i 1*0 X

Рис. 1.11. Обозначение падающих и отраженных воли к получению волновых матриц связанных линий

где pi,2 - диагональные матрицы волновых сопротивлений подводящих линий; Uit2~ - падающие и отраженные волны напряжений на входе и выходе 2п-полюсника. Обращаясь к (1.4.7), запишем

где

(1.4.11)

1.4.12)

р1,2 =

По определению матрицы / [2] получаем

Преобразовав (1.4.13), имеем

(1.4.13) (1.4.14)

Между падающими и отраженными волнами на внешних

о .4.16)

Уравнения (1.4.15) и (1.4.16) по определению матрицы рассеяния S позволяют записать:

(1.4.17)

Итак, полученные формулы для вычисления матриц а, у, t, S дают достаточно полный набор матричных параметров отрезков МСПЛ. Вычисление а, у, t или s требует решения полной проблемы собственных значений матриц ZY и YZ, что не всегда возможно, особенно при работе на микро- или мини-ЭВМ. Поэтому в практике анализа и синтеза устройств на МСПЛ часто прибегают к упрощающим предположениям. Например, полагают, что R = G = О, и вычисляют матрицы у н S, используя хорошо отработанные подпрограммы отыска-

ния собственных значений и собственных векторов (36, 37] Другой путь - получение аналитических соотношений для всех элементов матриц двухпроводных, трехпроводных или даже п-проводных СПЛ с периодической однородностью (34, 38, 50-56].

1.5. Двухпроводные связанные полосковые линии

Двухпроводные СПЛ занимают важное место в практике построения разнообразных устройств СВЧ. Модели их строятся на основе знания матричных параметров отрезков СП.Г с неуравновешенной связью. Для их нахождения of j3Ha4HM напряжения и токи на входе и выходе двухпроводной связанной полосковой линии так, как показано на рис. 1.12.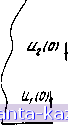

о--/ / /-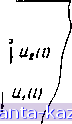

Рнс. 1.12. Отрезок двухпроводной СПЛ

Систс! I первичных параметров СПЛ в данном случае состоит и: 12 величин, описываемых матрицами Z и Y:

(/? +/(0L )(/?,2 + /c0L,2) (/?l2+/tl>Ll2) (/?22+/u)L22)

(G +/coC )(G,2-/(oC,2)

(G,2-/U)C,2)(G22+/(0C22)

(1.5.1) (1.5.2)

Дополняет систему первичных параметров длина СПЛ / в направлении распространения квази-Т волн. Следует заметить, что для СПЛ с неуравновешенной связью матрицы L и С