полоса пропускания нижних частот отстоит от частоты ш а также учесть выбросы выше номинального затухания в указанной шолосе .(см. рис. 10.04.2).

В результате функция (Ш.10.2) нривоянт к характеристике с чрезмерно увеличенной крутизной скатов на краях полосы пропускания со средней частотой шо. Хорошее яриближенне можно было бы получить с ломощью функции преобразования (10.10.2), добаВ1Ш множители, которые создадут нули функции f .(o)/u)c), достаточно близкие к оси ш (если вести рассмотрение с точки зрения комплексной частоты, см. гл. 2, §§ 2.03 и 2.04). Тогда эти нули можно было бы разместить так, чтобы растянуть полосу лропус-каиня инжннх частот iBieepx ib направле1Н-ни частоты Шо , и следовательно, получить нужный эффект.

Как оказалось, преобразования (10.06.1)-(Ю.Об.З) достаточно хорошо определяют характеристики опытных фильтров на встречных стержнях, в связи с чем дальнейшее исследование преобразования, применяемого прн расчете фильтров на встречных стержнях, не провоцилось.

Литература

1. Matthaei G L. Design of Wide-Band (and Narrow-Band) Band-Pass. Microwave Filters on Hie Insertion Loss Basis, IRE Trans. PGMTT-8, pp. 580-693 iNovember 1960).

2. Bolljahn J. T. and Matthaei G. L. A Study of the Phase and Filter rroperties ol Arrays of Parallel Conductors Between Ground Planes. Proc. IRE. 50. pp. 299-311 (March 1962).

3*. Matthaei G. L. Interdigitat Band-Pass Filters, IRE Trans, PGMTT-lOu pp. 9-491 (November 1962).

Cm. Зарубежная радиоэлектроника , ]в63, № 7.

Глава И.

ОСОБЫЕ ПРИЕМЫ, ОБЛЕГЧАЮЩИЕ СОЗДАНИЕ

ПОЛОСНОПРОПУСКАЮЩИХ ФИЛЬТРОВ НА СВЯЗАННЫХ РЕЗОНАТОРАХ, СОГЛАСУЮЩИХ ЦЕПЕЙ И ЦЕПЕЙ ЗАДЕРЖКИ

11.01. Введение

В трех .предыдущих главах излагались методы расчета различных типов полоснопропускающих фильтров, а также общая теория, позволяющая получить аналогичные расчетные методы яля других типов таких фильтров. гВ данной главе продолжается рассмотрение полосяошропуокающих фильтров на основе приемов общего характера н даются дополнительные сведения, шомогающие перейти от теории к практике.

В §§ 11.02-11.05 рассматриваются экспериментальные методы определения добротностей резонаторов и регулировки нх связей так, чтобы они соответствовали теоретически вычисленным величинам последних. Здесь же приводятся способы настройки собранных фильтров. В 11.06 и 11.07 из.тожены вопросы о потерях в резонатора.х, а также специальные сведения для расчета полоснопропускающего фильтра, когда важно свести к мн1нн.муму его потери на средней частоте.

§§ 11.08 и 11.09 содержат .дополнительные данные, облегчающие при.менение .методов, описаиных .в гл. 8 и 10 при расчете согласующих цепей, а в § 11.10 объясняется, как их можно использовать при расчете цепей связн для приборов с отрицательным солротивлетнем. В § 11.11 рассматривается и.римбнение этнх методов для расчета цепей типа полоснопропускающих фильтров с заданным временем зааерж.кн.

11.02. Измерение добротностей Q , Q. н Ql резонатора, нагруженного с одного конца

.На рис. ll.Q2.lfl .показан резонатор с инверторами сопротивлений Kl и Кг. Инвертор Кг разомкнут права, так что со стороны его зажимов с левой стороны оп представляет собой короткое за-

мыкаине, и поэтому даиную цепь можио заменить цепью, яока-занной на рис. 11.02.16.

(Крутизна реактивного сопротивления (см. § 8.02) такого резонатора paiBHa

лг = ю„ /-,

(11.02.1)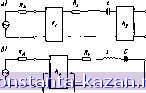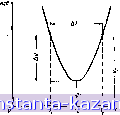

г. ,

Ряс. 11.02.1. Два эквивалентных резона Рис. II.02.2. Опреде.текие параметрол тора, нагруженных с одной стороны характеристики j<ob для резонатора,

нагруженного с одной стороны

а его ненагруженная .добротность <? =

(11.02.2)

Так как сояротнвленне Ил подключается к резонатору через инвертор Ки то оно становится равным Ry=K\IRA. Тогда нагруженная добротность равна

(11.02.3)

Внешняя добротность резонатора 0 определяется как добротность .при Rs-C г(т. е. прн (3 = оо), так что нагрузкой его служит только Ry.

Таким образом, внешняя добротность равна

Сс = -=

(11.02.4)

Предположим, что резонатор, показанный на рис. 11.02.1а и эквивалентный е.му на рис. 11.02.16, используется вместе с примыкающими к нему неоднородностями связи в волноводном фильтре типа, представленного на рис. 8.06.1, .или в фильтре с малыми апертурами связи, рассмотренном в § 8.07. (Предположим да-- па-

лее, что данный резонатор является первыш резонатором фильтра и что его внешняя добротность была рассчитана с 1помощьк> ф-лы (8.02.14). iB этом случае нужно произвести измерение (пара-.метров резонатора и убедиться, что его внешняя добротность совпадает с рассчитанной из величин элементов прототипа нижних частот.

Измерения добротностей Qu, Ql и резонатора, нагруженного с одной стороны, можно осуществить при помощи измерительной лннии с волновым сопротивлением Zo=Ra, используя .методику, описанную .ниже.

Поскольку резонатор обладает некоторыми собственными потерями, пре1дставленны.ми на рис. 11.02.1 сопротивлением iR era ксв на резонансной частоте h будет конечнысм. График ксв в области резонанса приведен на рис. 11Л2.2.

Если для схемы, изображенной а рис. 11.02.16, .выполняется неравенство

Ra f=f. Ra

>1,

(11.02.5>

то говорят, что связь резонатора выше критической. Показателем этого служит следующий факт: точка .минимума натряжения на измерительной линии при резонансной частоте io (частоте .минимального .ксв) будет отстоять примерно на четверть длины волны от положения минимума напряжения для частот, достаточно заметно отличающихся от резонансной').

Если неравенство i( 11.02.5) выполняется, то ксв при резонансе равен

Ra

(11.02.6)

В случае связи резонатора ниже критической ксв при резонансе равен

Vo=->I. (11.02.7)

L R.

Показателем этого служит тот факт, что положения минимумов налряження на из1мерительной лнннн будут шриблнзнтельно одинаковыми как для частот, заметно удаленных от резонансной, так

) При этом предполагается, что ширина резонансной кривой очень мяла, так что в пределах интересующего нас частотного диапазона изменение электрической длины измерительной линии невелико. Сдвиг минимума напряжения происходит вследствие того, что коэффициенты отражения на входе резонатора на резонансной частоте и на частотах, дсстагочно удаленных от резонанса^ отличаются по фазе на ISO ,

и для резонансной частоты'). Наконец, если при резонансе ксв Vo=l, то говорят, что связь резонатора равна критической.

Метоиика намерения добротностей резонатора включает, шрежде всего, измерение iMob ;рез01натоора iB окрестностях резонанса, а затем .построение такого же графика, KaiK .на рнс. 11.02j2.

Одновременно, .наблюдая сдвиг минимумов наП'ряжения на измерительной линии нрн расстройке частоты, необходимо определить, будет ли связь резонатора критической, выше .или иже Критической.

Прн связи больше .критической положения минимумов нацря-ження иа измерительной лнннн прн резонансе и на частотах, достаточно ущаленных от резонансной, будут отличаться примерно на Хо/4, а при связи меньше критической буяут примерно одинаковыми. Затем нз графика, приведенного на рис. 11.02.3а ири связи выше критической -или на рнс. 11.02.36 пря связи ниже критической, определяется параметр & v для данного значеиня ксв в середине полосы Vo я для 1ВЫ1йра нюй .велигаины N. Величина выбирается .произвольно, iho долЖ1на бьрть достаточно -большой, чтобы величина vc=Vo+AV заметно отличалась от Vo. При ювязн ниже .критнчеокюй значения Vo и vc заметно от.тичаются, .ковда Л'=1, поэтому на рис. Ilj02.36 шоказан только этот случай 2). Прц этом, если Vo>7, то берется значение AV= Vo-

После выбора величины Д!тодсчнтывается величина

(11.02.8)

Далее, как шоказано на рис. 11.02.2, определяется шнрнна я-олосы между частотами, на которых ксв равен vc. Затем рассчитывается ненатруженная добротность резонатора по ф-ле

(11.02.9)

М Предположения предыдущей есылки пр1Шснимы и элесь. Действительно, при связи ниже критической коэффициент отражении между 113мер11тел!,но 1 линией ii входом резонатора имеет одну и ту же фазу и при резонансе, и на частотах, достаточно удаленных от него. В результате минимумы напряжения на измерительной линии займут приблизительно одинаковые положения как на резонансной частоте, так и на частотах, удаленных от резонанса, при условии, что сдвиг частоты не настолько велик, чтобы заметно изменилась электрическая длина измерительной линии.

Если на резонансной частоте и на удаленных от нее частотах электрическое расстояние между резонатором и интересующим нас участком измерительной линии заметно меняется по сравнению с четвертью длины волны, то этот факт необходимо учитывать (гтри определелии того, является ли свяэь резонатора выше или ниже критической.

) Смысл величины n заключается в следующем. Уровень шаловин'ной мощности для ненагру жен ного резонатора чмеет место на частоте, на которой реактивное сопротивление резонатора равно его активному сопротивлению r. Кривые на рис. 11.02.3 а соответствуют реактивным сопротивлениям резонатора, равным xnra. При Л^=1 величина hf представляет собой ширину полосы ля уровне половинной мощности. При TV, отличном от единицы. &f будет приблизительно в n раз больше.

Есл связь резонатора выше критической, то внешняя добротность -раша

а наятружеиная добротность -

Vc+l - 121 -

(11.02.10)

(11.02.11)