Если связь резоиатара ниже критической, то внешняя доброг--шость равна

Q = V.<2 , (11.02.12)

а налружениая добрютность -

(11.02.13)

(Прн критической овязн пригодны приведенные выше формулы для случаев связи как выше, так и ниже жрнтнческон.

Чтобы лучше пояснить использование этих формул н соответствующих графиков, преяПоложи.м, что 1о=7, а овязь резонатора оказалась выще критической. Для соблюдения условия значительного отлнчня величин Vo и Vc желательно воспользоваться кривой N=i а рнс. 11.02.3а. Это же значение должно быть использовано в выражении i(l 1.02.9). Если бы величина Vo была еще больше, то вероятно было бы лучше нагрузить резонатор с двух сторон, как это описывается в следующем параграфе.

Измерения резонатора, нагруженного с одной стороны, можно также проводить с помощью фазового метода, описанного Гинз-тоном [1].

До снх !пор раоом'атрнвалнсь резонаторы .последовательного тнпа со связями, дейстоующимн .подобно yf-HHsepTopaM. Такой же анализ, проводимый на дуальной основе, применим к резонаторам параллельного типа i(co связями, (действующими подобно /-инверторам). (Поскольку расчет добротностей Qu, Qe и Qt осуществляется по данным измерений, то между этими двумя случаями нет никакой разницы.

Описашные выше экспериментальные методы весьма полезны для определения правильности выбора величин связи между оконечными резонаторами н нагрузками фильтра. Измеренные значения внешней добротности можно сравнить с величинами, вычнслея-нымн из элементов прототипа с сосредоточенными параметрами с ломощью выражений 1(6.02.14), (й.02.15) нлн (8.02.22), ;(в.02.23). Эти выражения вместе с методикой, изложенной в данном параграфе, применимы ко всем типам фильтров, рассмотренным в гл.8, а также к .ряду других типов фильтров со связанными резонаторами. При помощи указанных методов можно проверить .н отрегулировать величины оконечных связей тал, чтобы характеристика фильтра соответствовала характеристике прототипа нижних частот. Эти же .методы полезны также для проверки ненагруженных добротностей резонаторов, .что позволяет оценить полные потерн фнльтра в полосе пропускания.

Еслн известны параметры .крутизны реактивного сопротивле-НИ.Я X .или реактив/ной пров01ди..моста Ь резонаторов, то эту методику можно .нопользовать и для проверки величин связей между всеми резонаторами фнльтра. Когда резонатор с примыкающими к нему связями выделен нз фильтра, а его параметры измеряются

при услоонн нагрузки с одной стороны (см. рис. 11.02.1а), толегка показать, что

RaQ>

(11.02.14)

в случае фнльтра с параллельным резонансом используется дуальное выражение

°--, (11.02.15)

л V л

где Ga - активная п.роводн,мость .генератора; S\ - па.ра(.мегр инвертора .проводимости, а Ь-параметр крутизны реактивной про-водн,мостн.

Рассмотрим, например, фильтр тнпа, представленного на рнс. 8.05.1. Согласно ф-ле (8.14.16) параметр крутизны .реактивной проводимости таких резонаторов равен Ь=.(я/2)Уо. Если положить Ga = Yo, то выражение .(11Л2.15) принимает .вид

(11.02.16)

Таким образам, измеряя добротность Qe подобного полоскового резонатора, связанно(го с линией, как показано на рис. 11.02.4, можно найтн величину У/Уо (ДЛя данного раз.мера емкостного за-

К ите/штттй пинии

Енштшй sakp

Рис. 11.02.4. Одна из возможны.\ схем для экспериментального определення зазоров связи между резонаторами в полосковом фильтре типа, приведенного и а рнс. 8.05.1

зора связи. Используя схему измерений, приведенную на том же рисунке, М0Ж1НО найти величину зазоров связи, необходимую для получения значений Ус, определяемых выражениями (8..05.1) - (8.05.3). Эти методы будут, разумеется, пригодны и для других типов фильтров. Онн затрагивают, главным образом, экспериментальную подстройку связей резонатора до нужных величин. Вопрос получения точной резона1Нсной частоты рассматривается ниже в § 11.05. Следует подчеркнуть тот положительный факт, что подстройка резонаторов обычно .мало влияет на величину я связей. Наибольшая точность описанной здесь .методики наблюдается, когда добротности относительно большие. Однако в .некоторых случаях она может оказаться полезной, даже прн очень незначительных добротностях (например, лри Oi=20 нли около этого). - 123 -

11.03. Измерения параметров одиночных резонаторов, нагруженных с обеих сторон

В определенных условиях бывает значительно выгоднее проводить измерения резонатора, нагруженного с двух сторон (рнс. 11.03.1), а не с одной стороны (см. рис. 11.02.1). .Величины намеряемых .ксв обычно оказываются не столь большими, и в некоторы.х случаях резонансная частота одиночного резонатора, на-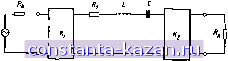

Рис. M03.I. Резонатор, нагруженный с двух сторон

груженного с двух сторон, может быть точ.но такой же, как у резонатора в многорезонаторном фильтре. Вот лочему в таких случаях этот метод позволяет ироверить как величину связн, так н резонансную частоту резонаторов многорезонаторного фильтра. Вопрос настройки будет рассмотрен более лошробно в § 11.05. Сейчас же заметим, что для -проверки указа.нным способом связей не только оконечных, но и внутренних резонаторов фильтра необходимо знать параметры крутизны резонаторов.

Для схемы на рнс. 11.03.1 внешней добротностью fC?c)i будем называть добротность для случая, когда цепь .нагружается только на сопротнвленне Ra слева (т. е. сопротивление Ra справа удаляется, так что цепь становится разомкнутой, и RsO). Аналогично (Qe)2 назовем внешней добротностью для случая, когда цепь нагружается только на сопротивление Ra справа. За.метим, что если параметры ИНверторов Kt ,и xz различны, то добротности (Qe)i и (Qe)2 тоже бу1дут рэзличагься. .Ненагруженная добротность резонатора (? равна его добротности для случаи, когда обе нагрузки Ra как справа, так слева удалены, и единственной активной нагрузкой резонатора служит сопротивление Rt, обусловленное его инутреннимн .потерями (ом. рис. 11.03.1).

.Нагруженная добротность резонатора, нагруженного с двух сторон, равна:

Qi=-i---: (11.03.1)

(11.03.2)

где /о - резонансная частота резонатора, а {&1)[злб] -ширина полосы, а границах которой затухание прн передаче через резо--натор превышает затухание на резонансной частоте на 3 дб. Затухание, вносимое резонатором прн резонансе, равно

= 101g

(11.03.3)

Определение добротностей (Qe)i, (Qe)2. Qu Ql., приведенное выше, подходит для любого резонатора - последовательного Нлн параллельного типа. Выражения (11.03.1) -(11.03.3) также применимы независимо от вида резонаторов.

Связи резонатора можно проверить, если рассчитать теоретические значения величин Ql и (LaK а затем, измерив эатухаяие, сравнить измеренные н рассчитанные значения (H)i3as] Ф'-е <11.03.2)]. Однако легче выполнить непОсреиствевные измерения КСВ.

Если экспериментальная методика, описанная в § 11.02. приме-ияется для измерения ксв с левой стороны схемы, приведенной на рис. 11.03.1, то добротность {Qe)\ можно определить в.месте с кажущейся ненагруженной добротностью, которая равн.ч

(QJi = ---г~- (И-03-4)

Аналогично, если измерение ксв производится с правой стороны той же схемы, то можно получить добротность (С?е)2 вместе с кажущейся ненагруженной добротностью (Q )2:

(11.03.5)

(Q ).

На резонансной частоте ксв с левой стороны указа'ннон схемы будет равен

(Vo).

критической

а С правой стороны -

или -

свяэь выше (V )-

(Q.)i

(QeU

Qu + Шг

-(ад.

(11.03.6) (11.03.7)

Так как значения добротностей ((?<.)[ н (qejz найдены непосредственно нз измерений, как описано выше, то добротность Qu можно рассчитать с помощью ф-л (11.03.6) илн (11.03.7). Однако .использование для этой целя нагрузки с одного конца по способу, изложенному в § 11.02, обычно дает большую точность. Если нзве-- 125 -

стно, что значение Qu велико по сравнению с (Q<,)i и (Q<,)2, те удобнее измерить, например, величину (Q,) а затем рассчитать (Q.)! по ф-ле (11.03.6), считая Qu = °<=.

На рис. 11.03.2 показано, как с помощью описанной выше методики можио проверить резонатор такого фильтра, например, приведенного на рис. 8.05.1: допустим, это четвертый резонатор шестирезонаторного фильтра, и нужно выяснить, соответствуют ли емкостные зазоры Дз4 и Д величинам JiifY и / /Ко, рассчитанным с помощью ф-лы (8.05.2).

пинии

парке

Рис. 11.03.2. Схема для испытаний псшоскового резонатора с нагрузкой на обоих концах.

Прояолимостъ нагрузки рввна ТГь

Посредством указанных выше измерений находят внешние добротности (Ср)з4 н (Qe) при нагрузке резонатора соответственно с левого н правого конца, как показано иа рнс. 11.03.2, После этого определяют соответствующие величины /34/0 и /45/0, используя выраженне (11.02.16) в виде )

bJ+J-,/-=-

Если значения У;, j+i/Vo не соответствует расчетным, то величины зазоров следует изменить так, чтобы добиться нужного результата. Резонатор на рис. 11.03.2 будет и.четь одну и ту же резонансную частоту н в случае режима работы, показанного на рисунке, и прн работе в многорезонаторном фильтре тнпа, приведенного яа ряс. 8.05.1. Поэтому, после того как резонансная частота резонатора проверена при правильных зазорах связи, можно, если это необ.чоцммо, откорректировать длину стержня резонатора для получення желаемой резонансной частоты. Способы подстройки других типов фильтров рассматриваются в § 11.05.

Данный .метод особенно удобен длн полосковых резонаторов, рассмотренных в § 8.05, поскольку их легко измерить раздельно н затем собрать вместе в сложный многорезонаторный фильтр. В случае аналогачных волноводных фильтров, описанных в § 8.06, .может оказаться целесообразным построить экспери.ментальный

) Как указывалось в § 11.02. это выражение основывается на том, что параметр крутизны резонатора равен 6-(л/2>Уо.. вак и. в; случае фильтров, рассмотренных в § 6.05.

резонатор с диафрагмами связи, вмонтированными в соединительные фланцы. При этом проверяемые диафрагмы легко вынуть н изменить нх размеры в соответствия с результатами испытаний.

11.04, Испытания С1шмет1шчных пар резонаторов

Большинство фильтров ОВЧ являются симметричными, в силу этого для каждого резонатора с заданными связями на одном конце фнльтра имеется такой же резонатор с такими же связями на другом его конце. Проверку связей в фильтре (а -иногда н точную проверку настройки резонаторов) можно осуществить, разобрав фильтр, соединив попарно одинаковые резонаторы и испытав каждую шару ои1Нов|ремвиню. Особое првм.мущество этого метода) перед методами, рассмотренными в §§ 11.02 и 11.03, заключается в там, что оэффищнент овязн k [ом. выражения (8.02.16) и :(8.02.24)] между резонаторами можно ошределить, не аная па;ра1метров крутизны резонаторов (1ам. § 11.02). Кроме того, в большинстве случаев получаются те ярко выраженные точки хорошей гаередачн (низкого кюв), так что для получения необхояимых данный потребуется меньшее число намерений.

В качестве примера рассмотрим симметричную пару объемных резонаторов, показанную на рнс. 11.04.1. Будем считать, что Qu -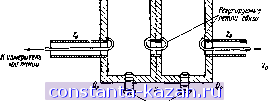

Настрспные биты

Рис 11.04.1. Симметричная пара объемных резонаторов с петлевыми связями.

Сопротивление нагрузки и изыерте.чьноП линии равно Zo

ненагруженная добротность, а Qe-внешняя добротность каждого из резонаторов, нагруженного на свою примыкающую (внешнюю) нагрузку (при Qu -оо); k - коэффициент связи между двумя резонаторами.

Кон (S. в. Cohn) н Шимизу (Shimizu) (3] показали, что затухание симметричной пары резонаторов равно

) Дишед (Dishal) (2] рассматривал аналогичную методику, но с использованием несколько иной терминологии.