ментами н последовательными емкостными связями последние можно рассматривать как часть инверторов тнпа, представленного на рис. 8.03.26. При этом отрицательная емкость инвертора компенсируется параллельными емкостями смежных резонаторов, о при подключеннн резонатора к активной нагрузке отрицательную параллельную емкость со стороны активного сопротивления скомпенсировать нельзя. Таким образом, влияние емкостной связи на настройку будет различным прн ее осуществлении между двумя параллельными резонаторами с сосредоточенными параметрами и между резонатором н активным сопротивлением. Этот вопрос рассматривался ранее в связи с ф-лами (8.14.32) -(8.14.34).

Прн относительно сильных связях коррекцию настройки можно выполнять, перестраивая поодиночке резонаторы (они испытыва-ются поодиночке при подключении к активным нагрузкам) на несколько другие частоты, вычисляемые на основе положений, изложенных выше при выводе ф-л (8.14.32) и (8.14.34). Прн относительно слабых связях (случай узкой полосы) требуемая коррекция будет незначительной н ею можно пренебречь.

Для фильтров, показанных иа рис. 8.05.1, 8.06.1, 8.07.1, 8.08.1. 8.10.3, трудности, отмеченные в предыдущем абзаце, не возникают, поскольку все эти фнльтры состоят из однородных линий передачи с соответствующим образом расположенными неоднородностями. Инверторы здесь имеют тот же анд, что на р с. 8.03.1в. 8.03.2г или в табл. 8.03.1. Отрезки линий отрицательной длины <р, входящие в инверторы, обладают таким же волновым сопротивлением, как и лииин резонаторов т нагрузок. Следовательно, указанные отрезки лнннй можно одинаково хорошо учесть в резонаторах илн в согласованных нагружающих линия.х. Поэтому, когда резонатор с волновым сопротивлением Zo вынимается из внутренней части многорезонаторного фильтра и испытывается между согласован-Hu.vtH нагружающими лнниямя, имеющими то же во.тновое сопротивление Z , то ошибки в настройке не будет, независимо от того, являются ли связи слабыми или сильными. Например, настройку резонаторов для фильтров вида, приведенного на рис. 8.05.4а, можно проверить, испытывая каждый резонатор (см. рнс. 11.03.2) и используя точно такие же зазоры связи на каждом конце, какие должны быть при установке резонаторов в многорезонаторный фильтр. Фактически нспытан-ие этнх резонаторов проводилось снм-.четричными парами (см. § 11.04).

Настройка резонаторов и поодиночке, и попарно дает высокую точность. После испытания резонаторов длины стержней были скорректированы для получения точного значения требуемой частоты настройки. При использованяи данной методики не требуется никаких настроечных винтов. Во многих случаях допуски оказываются не очень жесткими, что позволяет на основе опытного (испытанного) образца организовать массовое производство фильтров этой конструкцян без каких-либо настроечных винтов нли других приспособлений для настройки.

Узкополоеные фнльтры с параллельно связанными резонаторами типа, приведенного на рнс. 8.09.1, можно настроить, используя иэмернтельиую линяю, как было описано /выше гари рассмотрении схемы яа рис. 11.06.2. На рис. 11Л5.4 показано .возможное размещение яаспросчных винтов (для ф.ильтров этого тиша. После настройки резонатора п винты оконеиного звена п, п+1 должны быть вывернуты 1до уровня наружные заземленных пластин.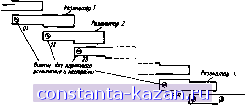

Рис. 11.05.4. Расположение винтов для настройки узкополосного фвльтра с параллельно связанными резонаторами

Обычно нет необходимости настраивать шкроиополооные фильтры такого типа, поскольку требованяя к точности синхроняой настройки понижаются по мере увеличения ширины полосы, и ошибки в настройке одного резонатора относительно других сравнительно мало влияют на характеристику фильтра в целом. Если средняя частота полосы пропускания не совпадает с требуемой, то длины всех резонаторов должны быть изменены на одну и ту же величину, которая рассчитывается так, чтобы получить требуемый Сдвиг средней частоты полосы пропускания.

11.06. Расчет потерь рассеяния на средней частоте полоснопропускающих фильтров

В § 4.13 были изложены необходимые данные для расчета потерь полоснопропускающих фильтров в середине полосы пропускания. В дополнение к ним приведем еще один лолезный пример расчета.

Пусть необходимо сконструировать шестнрезонаторный полоснопропускающий фильтр с шириной полосы 10% н величиной пульсаций чебышевской характеристики 0,1 дб н допустим, что найденные значения добротностей резонаторов иля .предлагаемой коист-рунцин ф.нльтра .оказались равными при6л1ивнтельяо 1000. Требуется апре(делить затухание в серешине полосы шронуокання, обусловленное потеря.мя <рыхьтшл в фильтре.

Для этого случая подходят график на рис. 4.13.2. Иэ него для я = 6 н при величине пульсаций чебышевской характеристики 0,1 дб получаем Св=4,3. Согласно -выражению (4.13.2) добротность элементов в соответствующем фильтре-прототипе ннжннх частот на частоте среза (uj равна

Q=i Qp=(0,10)(1000)=: 100,0,

ГДЕ 1И - относительная ширина полосы полоснопропускающего фильтра, а Qbp= Q - ненагруженная добротность его резонаторов. Тогда согласно ф-ле (4.13.3) коэффициент рассеяния

d = = -5-=0,01, Q 100

где в соответствии с данными рис. 4.13.2 прототипы предполагаются пронормированными та1 и.м образом, чтобы и',= 1. Далее согласно выражению (4.13.8) увеличение затухания в середине полосы, обуслотленное шотерямп рассеяния, приблиэителыно paiBHo (Д 8,686 С„ d = 8.686 (4,3) (0,01) = 0,37 дб.

Как было указано в § 4.13, за.тухание, обусловлежтое шотеря-.чн рассеяния на крайних частотах полосы пропускания, может быть примерно в 2-3 раза больше пол\чен ой величины, т. е. поряд.ка 0,741,1 дб.

Следует отметить, что иногда полезно проделать указанные вычисления в обратном порядке с целью определения ненагруженных добротностей резонаторов полоснопропускающего фильтра по измеренному приращению затухания фильтра в середине полосы, обусловленному потерями рассеяния.

Из ф-л 4.13 получаем

Существует несколько способов определення величин ненагруженных добротностей, которые *1Спользуются прн расчете затухй-ния полоснопропускающего фильтра. По одному иэ них добротность вычисляется на основе измеренных потерь в середине полосы реальных фильтров, как указано в предыдущем абзаце. Другой способ - проведение лабораторных испытаний образца резонатора для выбранного типа фильтра по методике, описанной а § 11.02. Третий способ - расчет ненагруженной добротности по данным гл. 5 для коаксиальных, полосковых и волноводных устройств.

Однако следует помнить, что теоретически возможные значения добротностей редко достигаются на практике. Это происходит вследствие шероховатости металлических поверхностей, коррозии, а также нз-за дополнительных потерь в элементах связи, которые трудно полностью учесть. В некоторых конструкциях полосковых фильтров фактические добротности обычно составляют около по-- 136 -

ловины их теоретических значений. В случае волноводных фильтров совпадение теории н практики оказывается несколько лучшим, но все же, как правило, необходимо принимать во внимание, что добротности в реальных фильтрах всегда будут меньше нх оптимальных теоретических величин.

Ряд других вопросов, касающихся потерь рассеяния в фильтрах, рассматривается в следующем параграфе.

11.07. Расчет узкополосных фильтров с пшнимальными потерями в середине полосы пропускании и заданным аатуханием в полосе запирания

В различных практических случаях, например прн разработке преселекторов для супергетеродинных приемников, требуются узкополосиые фильтры с возможно меньшими потерями в середине полосы пропускания и защавным высо- -

КИМ затуханием на некоторой частоте по-г,.г# лосы аапираяия. Так, .для супергетеро-диннаго прием.н,нка с in рам ежу точной частотой 30 Мгц необходим фильтр /предварительной селекции ic высоким затуханием на частоте, отстоящей яа 60 Мгц от ореяней частоты полосы пропускания, для подавления помехи по зеркальному каналу. У этих прнемнииов в диапазоне овч шнрнна полосы сигнала обычно очень мала по сравнению с используемыми несущими частотами. Поэтому при расчете фильтра предварительной селекции все внн.мание приходится сосредоточивать .на вьшмиеиии указанных требований. .При этом фактичесии обеспечивается достаточная ширина полосы пропускания для узкого спектра принимаемого сигнала.

Допусти1.ч, что рассматриваемые ф.нльт1ры обладают достаточно узкой полосой пропускания, так что независимо от физической структуры пр.именяемых резонаторов н связей будет справедливо упрощенное частотное преобразование;

(11.07.1)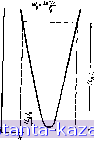

Рис. J1.07.]. Определение параметров (La.)o, (La)s и w . используемых в § 11.07

где

fo--

- 137 -

Здесь величина w представляет собой относительную ширину полосы пропускания, соответствующую полосе прототипа с граничной частотой й}[. Более важное значение имеет относительная щнрнна полосы в пределах которой затухание должно достигнуть заданного высокого уровня (La)s (см. рис. 11.07.1). Затухание (1л)о в середине полосы должно быть, разумеется, сведено к мнннмуму.

Многие расчеты, основывающиеся иа прототипах нижних частот, приводят к таким конструкциям полоснопропускающих фильтров, у которых затухание (а)о равно нулю, если нет потерь в резонаторах фильтра. Но когда в расчете учтены неизбежные потери в резонаторах, затухание (La)d всегда будет не равно нулю. При этнх условиях фнльтры с одинаковыми величннамн ws для заданного затухання могут иметь значительно отличающиеся друг от друга затухання в середине полосы (La) о.

Шнфмаи (Schiffman) [4] привел расчетные данные для двух и трехрезонаторных фильтров, которые позволяют получить в фильтрах м-нннмальные потери в середине noviocu для заданных значений w, н (La)s.

Кон [5] нашел длн общего случая произвольного числа резонаторов, что .малую величину (La)(i можио получить, е|Слн .фильпр рассчитать из прототипа .нижних частот оо следующими .параметрами:

Смысл этих параметров здесь тот же, что и в § 4.04.

Taj6 (Taub), Богнер (Bogner) [10], Фубини (Fubini) и Г11.1лемнн [II] исследовали фильтры с идеальными максимально плоской и чебышевской характеристиками при наличии потерь. Далее будет показано, что такие фнльтры обладают большим затуханием в середине полосы, чем рассматриваемые фн.1ьтры с одинаковыми элементами [для тех же самых значений ILa) ч^я и добротностей резонаторов).

Из выражений (11.07.2), (4.13.3) н (4.13.11) следует, что для фильтров, рассчитанных на основе элементов прототипа, приведенных в выражении (11.07.2), потери в середине полосы приблизительно равны

(11.07.2)

. 4,343 л

(11.07.3)

где qu - ненагруженная добротность резонаторов. Здесь .вел-ич.и-на (Z-a)c практически равна (Д/.а)о в выражении (4.13.11), так как этот тнп фнльтра идеально согласован в середине полосы при отсутствии потерь н очень близок к согласованию прн нх наличия. Величина w в ф-ле (11.07.3) представляет собой относительную ширину полосы пропускаиня, соответствующую полосе прототипа с граничной частотой <i)J. Именно она должна использоваться в расчетных выражениях гл. 8-11. Однако для задания рабочн.\ - 138 -

полос^,полезнее в нашем случае взять относительную ширину полосы W, С помощью выражений (4.14.1) (11.07 1) и (11 072[ о^улоГ язанымеждс1бой -Лщже !

.antll.Ii. 0

М1Шл7 по уча'еГ огда нз выражений (11.07.3)

4,343 antilg

20л

, дб.

(11.07.5)

На рис. 11.07.2 приведены графики, построенные на основе выражения ;(11.07.5) для разлнч- ных значений (La)! Отметим, smf что величина w,qu(LA)a лред-ставлеиа в функинн от числа ш резонаторов п. Таки.м образсм, для данных зиаченнй wg н qu ордината кривой пропорцно- нальна вел]ич.и е .потерь в середине полосы. Легко видеть, что оптимальное число резонаторов, необходимое для получення мнннмального затухания (La)!), зависит от заданной величины (La)s. При (La), =30 дб оптимальное число резонаторов п равно 4, в то время как для (Z.a) =70 дб, л=8.

Выражение (11.07.5). по которому вычислены графики на рнс. 11.07.2, .включает в себн ряд приближений, так что точность получаемых результатов улучшается с увеличением значений (La)s н произведения quw,). Для проверки практической применимости этого выражения рассмотрим типичный опытный расчет .фильтра со средними значениями величин (La), и quw

1) Выполненные Робинсоном (L. А. Robinson) примеры расчета пока зывают, что эти графики достаточно точны от nil ло таких значений п. где крквые начинают идти почти параллельно оси абсцисс, но далее, вследствие допущенных приближений, они не поднимаютси в правой части так круто, как

должны были бы.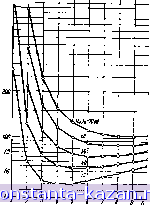

Рис. 11.07.2. График для определения

характеристик полоснопропускающих фильтров, рассчитываемых из равноэле-

ментных прототипов. п - число резонаторов. Значения да

им в аб *