Для параллельных ветвей, приравнивая реактивные сопротивлеиня, имеем

inL,--=-=--1---

(12.02.2)

что приводит к соотношению

(0,С( wai[gi

(12.02.3)

Длн последовательных ветв-ей, приравнивая проводимости, имеем

1 1 I I ш

1) С,--=-= -:----

что приводит к соотношению

(12.02.4)

(12.02.5)

Параметр крутизны х реактивного сопротивления резонатора Х=ш/--1/шС равен

, 1

(12.02.6)

аналогично параметр крутизны Ь реактивной проводимости резонатора В = шС--- равен

2 dm

- 0 =

(12.02.7)

Теперь выражение (12.02.3) для параллельной ветви приобретает вид

х, = -!-, (12.02.8)

а выражение (12.02.5) длн последовательной ветви -

(12.02.9)

Цепи, представленные на рис. 12.02.2, имеют те же уровни сопротивлений, что и прототипы на рис. 12.02.1. Чтобы перейти к другому уровню сопротивлений, каждое зиачеиие R п L необходимо умножить иа некоторый масштабный коэффициент, а каждое значеияе G и С - поделить на этот коэффициент.

12.03. Влияние потерь рассеяния ва характеристики полоснозапирающих фильтров

В этом параграфе вопрос о влиянии потерь рассеяния будет рассмотрен только для фильтров с сосредоточенными элементами, описанных в § 12.02, однако те же самые принципы применимы и для свч фильтров, приведеиных иа рнс. 12.01.1 и 12.01.2.

На рис. 12.03.1 сплошной линией показана характеристика затухания типичного полоснозапирающего фильтра (по любой из схем иа рис. 12.02.2) для идеального случая отсутствия потерь рассеяния в резонаторах. Однако в реальных фильтрах эти потери неизбежно будут иметь место; их влияние на характеристику фильтра проиллюстрировано иа том же рисунке пунктирной линией. Отметим, что теперь затухание иа частоте шо не стремится к бесконечности, а р„(.. 12.ОЗ.1. Влияние потерь рассеяиия в принимает иекоторое КОИеч- полоснозапираюшеы фильтре.

ИОе зиачеиие. Отметим так- / - характеристика идеального фильтра. 2-ха-же, что в полосах ПрОПуС- Р. Р а реально ф„.,ьтра

каиия фильтра, вблизи их границ, наблюдается значительное увеличение затухания вследствие рассеянии. Однако это приращение затухания в полосе пропускания быстро уменьшается по мере удаления частоты от полосы запирания.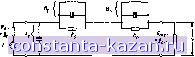

Рис. 12.03.2. Схема но.аоснозанирающего фильтра с учетом потерь рассеяния

На рис. 12.03.2 показан фильтр типа, представленного иа рис. 12.02.2, с сопротивлениями, добавляемыми для учета потерь рассеяиия в резонаторах. Если обозначить через Q i, Q 2... и т. д. ие-иагружеииые добротности резонаторов, то для параллельных ветвей пени

(12.03.1)

0. =

где Хи - параметр тора.

крутизны реактивного сопротивления резона-

Для последовательных ветвей цеп

Xt-- 1 bk

(12.03.2)

тде bh - параметр крутизны реактивной проводимости резонатора.

Для расчета затухания, которое обеспечивает фильтр в точке пика затухания (иа частоте щ), можно спользовать приближенную формулу, полученную на основе прототипа нижних частот <см. § 4.15):

(L ,) 20j lg(g,D,)-f 101g( j, 36, (12.03.3)

где Di=wia\Qui.

Обратные потеря иа частоте (Оо (потери отраженной мощности) рассчитываются по формуле

- -, дб. (12.03.4)

10 Ig

Они представляют интерес, если полоснозапирающий фильтр используется с целью обеспечения короткого замыкания или, наоборот, холостого хода для смежной с фильтром цепи на частоте шо-Влияние потерь рассеяния в полосиозапирающем фильтре можно оценить по формуле

Д1 ,=: 8.686

gig. I Вг/Вс Qui Qa.

л-МцВс

Qm , дб.

(12.03.5)

Эта формула определяет увеличение затухания, обусловленное потерями рассеяния, иа граничных частотах полосы пропускания <) и 0)2 и основывается на нескольких довольно грубых приближениях, рассмотренных в § 4.15. Хотя она лает невысокую точность, но может быть полезной при оценке порядка величины потерь рассеяния на границах полосы пропускаиня. При этом значение ALa в децибелах на частотах (Oi и юг, вычисленное по ф-ле (,12.03.5). ие должно отличаться от истинного больше, чем в 2 раза.

12.04. Приближенный метод расчета полоснозалираюицсх Свч фильтров с очень узкшпи полосами запирания

В данном параграфе описай в общих чертах метод расчета свч фильтров € очень узкими полосами запираиия-очень простой и вместе с тем универсальный. Тем ие менее в § 12.09 будет рассмотрен другой метод, который обеспечивает большую точность, осо-- Ш -

беиио в том случае, когда ширина лолосы запирания не очень мала. Однако в этом случае расчеты приводят к конструкциям, которые несколько труднее изготовить из-за наличия ступенек в передающей линии (чего не требуется при использовании излагаемого здесь метода). Для полноты изложения мы, однако, рассмотрим оба метода.

При реализации полоснозапирающего фильтра на линиях передачи более удобно использовать либо только параллельные, либо только последовательные ветви. Так, цепь на рис. 1.2.02.2о может быть преобразована в цепь, содержащую только параллельные ветви с резонансом последовательного типа, при помощи инверторов сопротивления (см. § 4.12), которые здесь аппроксимируются отрезками линии длиной в 90°, как

z. t

т г-I

-X-з:-----

Рнс. 12.04.1. Полоснозапирающий фильтр с паратлельными ветвями и четвертьволновыми соединительными линиями: а - сопротивления инверторов Z, одинаковы; б - общий случай с неодинаковыми сопротивлениями инверторов

показано на рис. 12.04.il. Ниже приведены параметры крутизны реактивного сопротивления этой цепи, выраженные через параметры прототипа нижних частот go. i. - gn+i и is>\.

Фильтр с одинаковыми сопротивлениями инверторов Z\.

1 1

1 Igd?!

2u (--чеш. \ 2fl / ш| gf ы(

{-нечетн. Ш, gogfOJ

(12.04.1> (12.04.2) (12.04.3)

Если п - нечетное, то Z, -Zo.

Этн формулы можно получить с помощью рис. 12.02.1 и 12.02.2, используя свойства четвертьволновых линий, которые можно рассматривать как инверторы сопротивлений.

Выходное и входное сопротивления цепи иа рис. 12.04.1а были приняты равными Zo. В случае фильтров с максимально плоской чебышевской характеристикой при нечетном п все инверторы сопротивлений могут быть одинаковыми и состоять из 90-градусяых линий, обладающ.их сопротивлениями Z, =Zo. Однако для чебышевских фильтров с четным п прототипы нижних частот будут несимметричными. Поэтому самый простой способ получения сим-- 185 -

метричного полоснозапирающего фильтра типа, показанного иа рис. 12.04.lo, заключается в том, чтобы сопротивления всех 90-гра-лусных Л-И1НИЙ Zi ие были равны Zo, а определялись из выражения

Еслн параметры крутизны, определенные с помощью ф-л (12.04.1) -(12.04.3), слишком малы или слишком велики для успешной реализации, их можио соответственно увеличить нли уменьшить, меняя сопротивлеиня 90-градусных линий. Формулы Л1Я общего случая имеют вид:

*1 1

и, go ei /Л . .г,- , у

/Z.z,...z, ,y ,

и-нечетн, l(itl)

m,g,Q

Если п - четное, то

.г„ /г„г,...г„ п2 ,

я если и - нечетное, то

Z, Z,Z,...Z ,

\Z,Z,...Z J

(12.04.5) (12.04.6) (12.04.7)

(12.04.8)

(12.04.9)

Они приводят к предыдущему случаю при условии, что Z,z2 =

ti... v, чн

Рис. 12.04.2. Полоснозапирающий фильтр с последовательными

ветвями и четвертьволновыми соединительными линиями-я - проводимости инверторов l-, одинаковы; б - общий случаи с неодинаковыми проводимостями инверторов

=... =Zn-i. Следует отметить, что когда величины Zi намного отличаются друг От друга, то в некоторых участках полосы пропускаиня получаются большие отражения, чем при постоянном уровне сопротивлений ZjZq, Это пронсход.ит потому, что электрическая длина 90-градусиых отрезков линий между резонаторами зависит от частоты, и, следовательно, этя отрезки приблизительно соответствуют идеальным инверторам только в ограиичеииом диапазоне частот. Если указаниые отрезки линий заменить ядеальным.и инверторами (см. § 4.12), то характеристики цепей, показанные на рнс. 12X14.1, были бы тождественны характернстякам соответствующих цепей иа рнс. 12.02.2 для всех частот.

Цепи, представленные иа рис. 12.04.2, дуальны только что рассмотренным иа рнс. 12.04.1. В иих используются последовательно включенные резонаторы, которые на резонансной частоте обладают высоким реактивным сопротивлением. Характеристики передачи фильтров обоих типов тождественны.

Фильтр с одинаковыми проводимостями инверторов Vit

< l go gl tti

ГН. \ Id / bigi D

If-неч€тн. to, gn/KH

Если n - четное, то

a если n - нечетное, то

У1=>о.

Для общего случая того же фильтра: Ьг 1 >1 go В,

/У'У'-У1-л go Т71- . \У Уг..у 12) ISi

Если п - четное, то Ко

.Г' /-У I lviK,...l J g.g ,

(12.04.10)

(12.04.11) (12.04.12>

(12.04.13)

(12.04.14) (12.04.15) (12.04.16)