Реактивную проводимость В диафрагмы связи нетрудно определить приближенно через коэффициент магнитной поляризуемости диафрагмы М'. Из табл. 5.10.2 получаем

(12.08.3>

(размеры а и Ь' определены на рис. 12,01.16).

Для диафрагм, длины которых I много меньше половины длины волны в свободном пространстве, прорезанных в стенках с бесконечно малой толщиной t, коэффициент магнитной поляризуемости AI=Ali можно найти из графиков, приведенных на рис. 5.10.4а. В реальных случаях, когда толщина t не является бесконечно малой и длина I не намного меньше половины длины волны в свободном пространстве, нужно вычислить коэффициент магнитной поляризуемости М\, который связан с величиной Al, приближенной эмпирической формулой:

(12.08.4)

где Ло -длина волны в свободном пространстве на средней частоте, соответствующая <о=шо, (р=<Ро и ?bg = ?ijo-

Условие резонанса для каждого резонатора принимает вид

4пЛ4,

(12.08.5)

2ni п

(12.08.6)

а L - длина резонатора.

Параметр крутизны реактивной проводимости Ь для каждого резонатора со стороны основной лииии передачи становится равным

6 = С(ф) П^(<р).

(12.08.7)

где f (ф) - определяется по ф-ле (12.05.5); С(ф)-по ф-.те (12.05.7), а М\ считается частотнонезависимым.

Пример расчета волноводного фильтра. В качестве примера применения изложенной выше методики рассмотрим расчет трехрезонаториого волноводного полоснозапирающего фильтра, использующего тот же прототип нижних частот, что и полосковый фильтр, описанный в § 12.07.

Пусть расчетная средняя частота фильтра fo=10 Ггц, а резонаторы в основная линия передачи выполнены а волноводе 1КЛ=90. У полоскового фильтра относительная ширина полосы - 200 -

составляла ш=0,05 по шкале частот 1см. ф-лу (12.08.1)]. В нашем примере используется полоса Ш; =0,05 по шкале .величин, обратных длиие волиы в волноводе [(см. ф-лу (12.08.2)]. Параметры крутизны реактивной проводимости для двух оконечных резонаторов и среднего резонатора можно определить по ф-лам (12.04.10) - (12.04.12), если положить YiYo. Они равны соответственно

= 12,528

- = 18,232

(12.08.8)

что в точности соответствует ранее вычисленным параметрам крутизны для полоскового фильтра. Волновые проводимости Уь шлейфов были выбраны равными Yq. Поэтому

С(Ф.О=С(фда) = = 25,056

(12.08.9)

= 36.464

Обращаясь к табл. 12.05.2, находим

%, + 90° = фда+90° = 159,5° Фо!.+90° = 163°

На частоте 10 Ггц величина Kga для волновода U7iR=90 равна 39,7 мм. Поэтому длины ii=i3 двух оконечных резонаторов и длина is среднего резонатора равны

L, = i,= 17.6

и= 18,0 мм,

Из выражения (12.08.5) можно определить, что коэффициенты магнитной поляризуемости (Л15)=(М| )з для диафрагм в оконечных резонаторах и коэффициент магнитной поляризуемости (.М,)2 для диафрагмы в среднем резонаторе равны

(12.08.10)

(12.08.11)

(Л1;),=(Л1;)з=2бб лл(

(M;j2 = 225 л

(12.08.12)

Прн расчете было решено использовать щелевые диафрагмы с закругленными краями (что соответствует второй сверху кривой на рис. 5.10.4а). Для определения размеров диафрагм вначале задавались их шириной') и)1 = Ш2=Ша=3,18 мм, а затем методом по-

*) Ширима щели w (см. рис, д.10.4а) обозначается тем же символом, что и относкгельная ширина полосы. Это - обычное обозначение для обеих величин. Поскольку расчет щели в данном коитекс-ге является побочным, сохранение обозначения w для ширины щели внесет меньше путаницы, чем изменение его.

следовательных приближений с помощью рис. 5.10.4а и ф-лы (12.08.4) вычислялась длина диафрагм. Так как заранее было известно, что их размеры будут проверены экспериментально (по методике, изложенной в § 12.06), то толщина диафрагм / в ф-ле (12.08.4) была принята равной нулю (что должно было вызвать иекоторое уменьшение размеров диафрагм). В предлагаемом способе выполнения этих вычислений ф-ла (12.08.4) приводится к виду

(12.08.13)

Далее из графиков, приведенных иа рис. 5.10.4а, для требуемых коэффициентов поляризуемости (М\)к определяются предварительные значения длин диафрагм Ih- Подставляя их в ф-лу (12.08.13), получаем уточненные значения коэффициентов поляризуемости (Ali)ft, с помощью которых затем по указанным графикам находят уточненные значения длин диафрагм Ih. Если требуется, данный процесс можно повторить, чтобы добиться большей точности. Однако, поскольку ф-ла (12.08.13) сама по себе является довольно грубым приближением, ценность получения высокой математической точности весьма сомнительна.

Ли А-А faiHSu SmHoladtt типа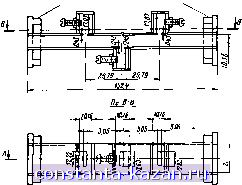

9 -i.

Рис. I2.0&1. Эскиз волноводнсго полоснозапирающего фильтра X-диапаэона (диапазон частот от 5,820 до 12.40 Ггц). Все размеры в мл - 202 -

п mm fгщ

Рис. 12.08.2. Вычисленная (сплсшная линия) и изиеренная (зачерненные кружки) характеристики волнсводнсго полоснозапирающего фильтра, изображенного на рис 12.08.1. Неэачернекнымн мр.Умкамн показана кривая потерь на спражение s полосе пропускаиня, вычисленная по нэнереииыи ксв

Описанным способом были получены предварительные значения длин диафрагм Л = з=10,9 мн и /2= 10,5 мм при ширине диафрагм К1 = ш2=Юз=3,18 мм. После испытаний, которые заключались в измерении ширины полосы на уровне 3 дб отдельно для 1 и 2-го резонаторов (методами, рассмотренными в § 12.06), определялись окончательные значения длин диафрагм; (1 = /з= 12,21 мм

и /2=11,62 JMJI.

В первом варианте фильтра расстояния между резонаторами . составляли но он оказался неудовлетворительным из-за взаимодействия между краевыми полями диафрагм различных резонаторов (что приводило к значительным провалам характеристики в полосе запирания). Поэтому был сконструирован второй вариант фильтра с расстояниями между резонаторами 3?.о/4. Размеры его показаны иа рис. 12.08.1.

Настройка этого фильтра велась по методике, изложенной в § 12.06. На рис. 12.08.2 проведено сравнение экспериментальной характеристики, измеренной в нескольких точках, с теоретической характеристикой фильтра, рассчитанной с помощью вычислительной машины. Как видно, результаты хорошо согласуются.

Вместе с тем из того же рисунка можио заметить, что величина пульсаций в полосе пропускания для расчетной характеристики равна примерно 1,2 дб вместо 0,5 дб, как это предусматривалось - 203 -

прототипом с сосредоточенными параметрами. Такое превышение величины пульсаций обусловлено частотной зависимостью линий связи между резонаторами. Если бы они были заменены идеальными инверторами сопротивлений, то величина пульсаций чебышевской характеристики стала бы точно равной 0,5 дб. Расчеты на вычислительной машине показывают также, что при использовании линий связи длиной W4 максимальная .величина пульсаций достигала бы примерно 0,7 дб. Максимальная величина пульсаций в 1,2 дб для расчетной характеристики, приведенной на рис. 12.08.2, указывает иа еще большую избирательность линий связи длиной 3iXo/i, используемых в данном фильтре. Применение методики расчета, рассмотренной в § 12.09, позволило бы учесть избирательные свойства линий связи так, что величина пульсаций оказалась бы очень близкой к ожидаемой'). Это достигается, однако, ценой того, что, согласно упомянутой методике, вдоль основной линии фильтра обязательно должны иметь место перепады сопротивлений, что усложняет изготовление фильтра. Если сопротивления основной линии и параметры крутизны резонаторов определяются согласно данным § 12.09, то процесс расчета остается таким же, как было описано выше.

12.09. Точный метод расчета полоснозалирающих фильтров с широкой и узкой полосой запирания

Здесь будет рассмотрев точный метод расчета полоснозапира-ЮЩ.ИХ фильтров, пригодный как для широких, так и для узких полос запирания. Приведенные расчетные выражения относятся к фильтрам со шлейфами длиной Хо/4, разделенными линиями связи длиной Ло/4 нли 3/.о/4, где м - длина волны иа средней частоте полосы запираиия. Пример фильтра такого типа приведен на рнс. 12.01.2. Теоретически ои может .иметь любую ширину полосы запирания, однако практически сопротивления шлейфов становятся нереализуемыми, если полоса запирания оказывается слишком узкой. При этом было бы желательно заменить -резонаторы в виде разомкнутых шлейфов (как показано на упомя-нутом рисунке) резонаторам.и в виде короткозамкнутых шлейфов с емкостной связью (как показано на рис. 12.01.1а) с теми же самыми параметрами крутизны. Хотя это вносит некоторые приближения в расчет фильтра, но зато позволяет получить реализуемые величины сопротивлений. Ранее уже отмечалось, что при расчете полосно-

) Расчетная методика, описанная в § 12.09, тючна, когда фильтр выполнен только из линий передачи и шлейфов. Однако в случае полоснозапирающи.: фильтров с узкой полосой запирания сйпротиаленин шлейфов становятся неприемлемыми, поэтому шлейфы необходимо заменять резонаторами с реактивными связями, что уже является приближением.

2) Материал данного параграфа содержится в работе Шифмана и Маттея 16]. Кроме того, там приведены дополнительные расчетные данные для некоторых типов фильтров, рассмотренных после написания этой книги.

запирающих фильтров с узкой полосой запираиия по методу настоящего параграфа требуются перепады сопротивлений в линии передачи, в то время как при расчете по методу, описанному в § 12.04, такие перепады обычно не нужны. Однако метод, который изложен здесь, обеспечивает более высокую точность расчета даже в случаях узких полос запираиия, когда применяется указанное выше приближение. Он позволяет произвести точный расчет фильтров типа, представленного на рнс. 12.09,1а. и дуальных

La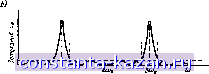

Рис. 12.09.1. Почоснозалирающий фильтр: а - п-шлейфный фильтр на передающих линия.\, полученный из л-элементиого прототипа ннжни\ частот; б- равнопульсирующая характеристика, определяющая среднюю частоту (Оо. параметр а и относительную полосу запирания W.

Длины всея шлейфов н соедиинтельных лнинй равны: Г.. (1) = 1 2 (111, + ш,): = глцй), где О - скорость i-нета н i-рБде paclipwnaiiCHMx; а= ctg <№t], 2о>); (о), - a ,),(i)

ИМ (состоящих ИЗ четвертьволновых короткозамкнутых шлейфов, включенных последовательно с четвертьволновыми соединительными линиями). Характеристики затухания таких фильтров связаны с характеристиками затухания прототипов нижних частот типа, приведенного на рис. 12.02.1, с помощью следующего преобразования ):

л to \

(12.09.1)

) Можно показать, чго другие методы расчета (2, 3] могут привести к цепям типа, показанного на рис. 12.09.1 а, характеристики затухания которых не являются преобразованием .уарактернстик затухания этих прототипов.