Тогда коэффициент уменьшения полосы пропускания равен

(9.08.5>

Он может быть найден с помощью графиков на рис. 9.08.2, построенных в функции от величины R, которая .равна отношению, (большему единицы) выходного сопротивления к входному для трансформатора-прототипа. Для узкополосных фильтров полоса пропускания по частотной шкале почти симметрична и. таким образом, ширина полосы определяет также ее границы (для узкополосных фильтров величина р приближается к 0,5, как в примере § 9.04). Для широкополосных фильтров уменьшение ширины полосы

Рис. 9.08.2. График коэффициента уменьшения полосы Р Б функции числа резонаторов п и произведения ксв неоднородностей R

Рис 9.08.3. Преобразование частотной перемещюй для получения приблиэи-TeibHti симметричной .характеристики.

не характеризует всего явления, и поэтому следует рассматривать отдельно смещение каждой граничной частоты. Это сейчас и будет показано.

Искажение полосы пропускания. Как будет видно из § 9.10, характеристика оказывается почти сим.метричной, если рассматривать ее как функцию не частоты, а переменной

(9.08.6)

(см. рис. 9.08.3). Там же показано, что для фильтров с высокой избирательностью (фильтров, соответствующих большому отношению R выходного сопротивления трансформатора к входному) показатель степени а приблизительно ра.веи - 32 -

a l-)-i-

( l).

(9.08.7)

где п - число секций трансформатора или число резонаторов фильтра.

Следует заметить, что случай а sail, соответствующий большому значению п, приводит к симметричной характеристике в функции от ДЛ.ИНЫ волны. Это было отмечено Коном [3], который исходил из других соображений. . Когда R приближается к единице, а стремится к .нулю для синхронно настроенных фильтров (ом. гл. 6) при всех значениях п безотносительно от частотных зависимостей связей. Таким образом, любая из кривых, приведенных на рис. 9.08.4, должна прохо-

56 I =ff *-

Piic. 9.08.4. График коэффициента искажЕиин полосы а в функции

среднего значения ксв неоднородности V . График получек п1тем соедииення планноА кривой расчетны.х точек для четырнадцати частных случаен

дить через начало координат. Аналогично выражение (9.08.7) определяет асимптоты для этих кривых. Выражение (9.08.6) может стать точным для двух граничных частот полосы fi и fz, если определить а как

lg(uyuf,)

(9.08.8)

где

Выражение (9.08.8) далее будет использоваться в качестве определения параметра а. Он был найден таким способом для четырнадцати совершенно различных фильтров с рассчитанными характеристиками. Эти фильтры име. число резонаторов гг=3-т-8. а у одного из фильтров был только один резонатор (nil); полосы пропускания изменялись от узких (ilO%) до средних и широких (85%). Четырнадцать указанных точек приведены на рис. 9.08.4, где построен график для параметров а в функции среднего значения ксв неоднородности

(9,08.10)

при.чем одиннадцать точек могут быть объединены плавной кривой, проходящей через нихили весьма близко к ним. Три остальные точки относятся к следующим случаям: одна точка соответствует фильтру с п=1 (см. § 9.10); из аы>ражения (9.08.7) -получаем aftf2, что Как раз имеет место в данном случае. Другие две точки, шоказаниые треугольниками, соответствуют фильтрам с неодинаковыми волновыми сопротивлениями отрезков линий, которые будут рассматриваться в § 9j1J.

Таким Образом, приходим к заключению, что кривая иа рис. 9.08.4 .может быть использована для определения коэффициента искажения полосы пропускания о для фильтров с одинаковыми сопротивлениями и с числом резонаторов п больше трех.

Из выражений (9.08.8) и (9.08.9) находим, что частотное смещение fm-fo определяется следующим образом:

6 fa-/. -ДЛ

Ig л=Ig (д y f J = а Ig (JM =a le

12+a \

(9.08.11)

Эта формула будет точной, когда выражение (9.08.8) рассматривается в качестве определения, что и было сейчас сделано.

С помощью ф-лы (9.08.11) построены графики (рис. 9.08.5), показывающие зависимость частотного смещения (fn-foj/lm от относительной ширины полосы пропускания w для различных значе-йнй .параметра а [когда а=0, смещение (fm-fo) тоже равно нулю].

На этом заканчивается .рассмотрение влияния замены перепада сопротивлений-реактивными элементами на положение границ полосы пропускания. Теперь рассмотрим, как такая замена влияет иа затухание в полосе запирания.

Затухание в полосе запирания. Здесь будет изложена простая методика для оценки крутизны скатов характеристики фильтра. Допущенные приближения позволяют довольно точно произвести такую оценку в пределах большей части характеристики, но точность оказывается .несколько меньшей вблиз.и границы полосы про-- 34 -

= зГир;рн~Ге, 1.0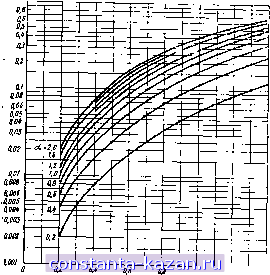

Zih График относительного смещения средней частоты от синдоон-ной частоты 6 в функции относительной олош ш для н™к^киТзн™. чений ц

описывГтГ|-лой1: 16.037 * ° фи-Ра

7 (./М

где /? - произведение ков неоднородностей:

2* - 35

(9.08.12) (9.08.13)

Здесь Т„ - Чебышевский полином п-то порядка, а ро - постоянная величина (см. §6.02), равная

m, = sin(il). (9.08.14)

Характеристика фильтра с реактивными элементами также оп-47еделяется ф-лой (9.08.112). Только при этом Д уже более не является шостоянной величиной, так как Vi будут функциями частоты вследствие частотной зависимости реактивных проводимостей (илн реактивных сопротивлений). Отсюда на любой частоте/ для фильтра с параллельным.и реактивнььми проводимосЛми, приведенного на рис. 9,03.1 б, получаем следующее выражение для V,-, когда все сопротивления линий оиинзковы:

н+iBi/y,) шт - (Bi/Vc) ihif)

(9.08.15,

Заметим, что для фильтра с последовательными реактивными сопротивлениями на рис. 9.03.1а вместо Bi/Kg надо подставить KuZo-

Для достаточно больших значений Vi и Bi ф-ла (9.08.15) приводит к приближенному равенству

yiVt)~(BMf- (-08.l6)

.9то равенство выполняется с точностью до 20% при

8% При В|>5, до 2% при В|>7 и до 1% при \В меньших значений \В нужно шользоваться Ф-лой (9.1

В|>3, до >8. Для

, нужно шользоваться ф-лой (9.08.15). Численное решение ур-ния (9.08.15) для /=/<, предста'нлено в виде кривой, отмеченной /1 = 1 на рис. 9.03.2.

Затухание фильтра в обеих полосах запираиия можно просто и довольно точно оценить, исходя из известного затухания трансформатора-прототипа. Согласно выражению (9.08.16) величина R является функцией частоты и, следовательно, приближенно можно написать:

~(fc/f) - , (9.08.17)

а согласно выражению (9.08.12) затухание необходимо умножать иа этот же коэффициент, когда R велико [если некоторые из значений Vi м.члы, то должна быть использована более точная ф-ла (9.08.16), а не выражение .(9.08.li6)l.

Таким образом, чтобы оценить затухание фильтра на заданной частоте, не слишком близкой к границе полосы пропуокания, можно Сначала найти затухание трансформатора в децибелах на со-втвегствугощей частоте и затем добавить к этой величине 20(п--+1) Ig iUf). йб, как уже было ранее установлено ф-лой (9.04.2).

Под соответствующей частотой здесь понимается частота / характеристики четвертьволнового трансформатора (см. рис. 9.08.1), которая получается из линейного пересчета частотной шкалы: - 36 -

Afi А/.

(9.08.18) (9.08.19)

в зависимости от того, находится ли частота f ниже первой граничной частоты fi или выше второй граничной частоты

Следовательно, затухание в полосе запирания фильтра может быть довольно точно оценено по характеристике трансформатора-прототипа. Однако чаще должна решаться обратная задача. В зтом случае в число задаваемых величии может быть включено затухаДне в полосе запирания фильтра иа некоторой частоте и, например, величина .пульсачнй в полосе пропускания, а также ширина полосы. Нужно найти минимальное число резонаторов п, обеспечивающее требуемые xapaiKTepHCTraai. Такая задача может быть строго решена только для прототипа (см. гл. 6). Чтобы определять число резонаторов п полуволнового фильтра с реактивными свнзями, которое необходимо для получения заданных: неличины пульсаций я полосе пропускания, ширины полосы и избирательности (затухания в полосе запирания), приходится повторять решение задачи несколько раз, каждый раз задаваясь новым значением п до тех пор, пока характеристики фильтра не удовлетворят заданным требованиям. При возможности использования выражений (9.08.17) и (9.04.2) задача решается быстрее, как было показано в примере § 9.04. В остальных случаях необходимо использовать выражения (9.08.13) и (9.08.116), причем численное решение упрощается с помощью графика, приведенного на рис. 9.03.2. Обычно нет необходимости искать решение для всех Vi и достаточно решить задачу только для одного среднего значения ксв неоднородности V , определяемого выражением (9.08.10). Это экономит время при вьЕПОлненин расчетов. Такой метод применен в последнем примере следующего параграфа.

На это-и заканчивается изложение материала, необходимого для выбора трансформаторов-прототипов, нз которых можно получить фильтры с заданными характеристиками. Теперь кратко изложим методику расчета.

1. На основании заданных требований выбирается четвертьволновый транСформатор-прототнп, из которого можно получить фильтр с характеристикой, близкой к заданной, при этом у выбранного трансформатора величина пульсаций в полосе пропускания должна быть равна величине пульсаций, задаваемой для фильтра.

2. Из рис. 9.08.2 определяется величина § и вычисляется величина w=Wq. Если полученное значение ю не равно задалному, то нужно повторить вычисления с другим трансформатором, имеющим другую ширину полосы Wq. Этот процесс повторяется до тех пор, пока значение w не станет равным заданному.