Соответствующая формула для ИЖГ сферы, укрепленной вблизи короткозамыкающей стенки в полосковой структуре с волновым сопротивлением Z, приведена ниже:

Q (I20n)-di

(17.07.3)

где цо-магнитная проницаемость среды в области около сферы; с1 - расстояние от центрального полоскового проводника до наружной заземленной пластвны.

На рис. 17.07.6 приведены кривые добротности Qe ИЖГ резонатора, используемые прн 2=60 ом. Заметим, что эти кривые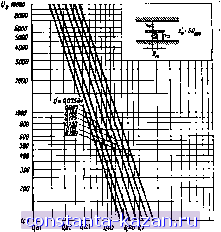

аг1) ,дтм.

Рис. 17.07.6. График добротности Qe в функции диаметра сферы для сферического ИЖГ резонатора в симметричной полосковой .линии

дают значения Qr прн заданном расстоянии d (в дюймах) от центрального проводника до наружной пластины и заданном диаметре сферы Dm (также в дюймах). В случае использованил резонатора из какого-либо другого материала, а не из ИЖГ, илн в случае полосковой линии с волновым сопротивлеиием, не равным - 452 -

OJnep ,=0,-

(17.07.4)

50 ом, величины, получаемые из графика, должны быть пересчитаны с помощью выражеиня

(*sW 50

(ад (z- )

где (2 )исп - волновое сопротивление используемой линии, а (А1,) ИЖГ/(Л1.)исп - отношение намагниченности насыщения ИЖГ к намагниченности насыщения используемого материала. Формула (17.07.3) (иа основе которой построены рассматриваемые кривые) выведена в предположении, что полосковая линия была ограничена с каждой стороны с помощью магнитной стенки (это

Sr , мм

Рис, 17.07.7. Теоретические (сплошная линия) и экспериментальные (крестики) значения добротности С для ИЖГ резонатора в полосковой линии. Все размеры в мм

означает, что краевых полей нет), и поля около полоскового внутреннего проводника совершенно однородны. Разумеется, если полосковая линия настолько узка, что сфера попадает в область краевых полей, то такое приближение приведет к заметным ошибкам.

На рис. 17.07.7 представлены вычисленные и экспериментальные данные, полученные Картером [3] при проверке ф-лы (17.07.3) на частоте 3000 Мгц. Прн этом он использовал показанную на ри. сунке структуру. Следует отметить, что сфера для каждого опыта монтировалась примерно на расстояини ЗЛ25 мм (0,125 дюйм.) от короткозамккутого конца. Как оказалось, размещение сферы слишком близко к короткозамыкающей стеике вызывает искажение характеристики сферы, а размещение ее слишком далеко от стенки - чрезмерную реактивность, которая приведет к уменьшению связн со сферой. Как можно видеть, рис- 17.07.7 .иллюстрирует достаточно хорошее соответствие теоретических и экспериментальных данных.

Другая экспериментальная работа Картера [4] показала, что наличие смежной щели (как в фнлыре на рис. 17.07.3) приводит к уменьшению свяэи со входом цепи. Это вызывает увеличение внешней добротности примерно на 20% или несколько более по сравнению с ее величиной в отсутствие щели. Таким образом, прн расчете полосковой линии и размеров сферы должен быть сделан некоторый допуск на указанный эффект, чтобы реализовать требуемую внешнюю добротность,

В ф-ле (17.07.3) внешняя добротность обратно пропорциональна сопротивлению линии Zj. Это объясняется тем, что для данного диаметра сферы и расстояния d от наружной пластины до центрального проводника, концентрация высокочастотного магнитного поля вокруг сферы будет тем выше, чем уже полосковая линия (однако, еслн последняя становится слишком узкой, наличие краевых полей нарушает эту картину). Формула (17.07.3) и кривые на рис. 17.07.6 получены в предположении, что полосковая линия является однородной и нагружена на сопротивление, равное ее волновому сопротивлению. Однако если в окрестности сферы используется короткий отрезок линии с волновым сопротивлением Zj нагруженный на значительно меньшее активное сопротивление Ra, то можно получить более низкие значения внешней добротности. Так, если Qe-внешняя добротность, когда линия нагружена на активное сопротивление =Zj, то внешняя добротность при нагрузке, равной Ra, приблизительно равна

(17.07.S)

При этом, конечно, предполагается, что отрезок линии с сопротивлением Zj (с которым связана сфера) короче четверти длины волны и, значит, рассогласование его волнового сопротивления Zj с нагрузкой Ra не приведет к появлению чрезмерной реактивности. Как следует из выражения (17.07.5), связь может быть сделана более сильной (т. е. скорректированную величину добротности Q, можно снизить), если уменьшить сопротивление нагрузки Ra. Этот результат находится в соответствии с ф-лон (17.07.1). Таким образом, в тех случаях, когда трудно получить достаточно ннэкую величину Qe, уменьшение сопротивления Ra дает желаемый результат. Если значение сопротивления внешней нагрузки не допускает такой возможности, то для получення нужной величины Ra можно .использовать ступенчатый трансформатор.

Для экспериментальной проверки величин внешних добротностей, а также ненагруженных добротностей удобны методы, изложенные в § 11.02.

Расчет конструкции для заданных коэффициентов связи. Определение расположения ферромагнитных резонаторов и размеров .отверстий для того, чтобы получить заданные коэффициенты связи, является довольно сложной задачей, и в настоящее время нет - 454 -

никаких расчетных методов ее решения. Однако, используя экспериментальный метод испытания двухрезоиаторной структуры, описанный в § 11.04, практически .нетрудно определить необходимое расположение сфер (расстоявие между ними) и раз1меры отверстия. Некоторые результаты, приведенные в § 17.08, должны послужить в .качестве полезного руководства для данной цели.

Помимо обеспечения достаточной связи между сферами, существуют и другие требования к расчету, а именно: получение достаточно высокой развязки вне резонанса и достаточного промежутка между сферами (разнесения сфер) с тем, чтобы каждая нз них не приводила к искажению подмагничнвающего поля в области расположения другой сферы и нарушению однородности поля в ней (а значит, и к возбуждению паразитных типов колебаний). Экспериментальные результаты в примерах, приведенных а § 17.08, могут быть полезны для удовлетворения обоих этих требований. Что касается расположения сфер, то разнесение их на расстояние (между центрами сфер), примерно равное трем диаметрам, по-видимому, будет достаточным.

Влияние изменения параметров фильтра (пересчет параметров). Важно также знать, какое влияние иа внешние добротности крайних резонаторов и иа коэффициенты связи между резонаторами оказывает -изменение размеров структуры, намагниченности насыщения и рабочего диапазона частот. Это помогло бы проектировщику использовать сведения, полученные при расчете одного фнльтра, для расчета других фильтров с несколько иными параметрами.

Как упоминалось ранее в этом параграфе, эквивалентные цепи иа рис. 17.02.3 могут быть использованы при анализе фильтров с ферромагнитными резонаторами. Следовательно, выражения (17.02.11)-1(17.02,13) также применимы, и мы можем представить их здесь в виде

(Qe)B =

(17.07.6) (17.07.7) (17.07.8)

где Xj, j+i- взаимные реактивные сопротивления, а Xj - параметры крутизны резонаторов. Взаимные реактивные сопротивления можно представить в виде

1.Ж = о1*оЖ,.,. (17.07.9)

где Шо - резонансная круговая частота; цо - магнитная проницаемость воздужа, гн/ед. длины; Wj, j+i - масштабный множитель, - 455 -

зависящий от размеров структуры н имеющий размерность длины. Тогда из выражений (17.07.6) и (17.07.9) получаем

Картер [26] показал, что в общем случае, если связь с ферромагнитным резонатором осуществляется прн помощи переменного магнитного поля с линейной поляризацией, то справедливо соот-иощение

Здесь Vm -объем сферы;

Y - гиромагнитное отнощение и

(17.07.11) (17.07.12) (17.07.13)

где А - напряженность переменного поля около резонатора, вызванного током Iaj протекающим в нагрузку На. Параметр Ощ. как это видно, имеет размерность 1/ед. длины.

Приравнивая выражения (17.07.11) и (17.07.10) и решай полученное уравнение относительно параметра крутизны резонатора XI, получаем

(17.07.14)

Полагая далее, что x,=Xi, из выражений (17.07.7), (17.07.9) и (17.07.14) имеем

-./+1- о> (Г„)> Проверяя размерность выражения (117.05.15), находим

(17.07.15)

(17.07.16)

где А - безразмерный множитель, оторый определяется только относительными соотношениями между размерами различных частей схемы и ие изменяется при пропорцнональном изменении размеров всей схемы.

Используя несколько другой подход, можно заключить, что изменение величин М, резонаторов должно быть аналогичным изменению числа витков катушек в цепи, приведенной на рис. 17.07.5. В этом случае взаимное реактивное сопротивление Xoi для - 456 -

связи с нагрузкой должно быть пропорционально А1 а взаимные сопротивления Xj, j.i для связи между резонаторами - пропорциональны величине . Исходя из указанного подхода, был проведен анализ, подобный -описанному выше. Он также приводит к выражению (17.07.16), что еще раз подтверждает справедливость данного выражения.

Из проведенного выше анализа может быть сделано несколько полезных выводов.

1. Пропорциональное увеличение или уменьшение размеров схемы не оказывает влияния на коэффициенты связи между резонаторами, хотя из выражений (17.07.11) - (17.07.13) следует, что внешние добротности крайних резонаторов Qe изменяются. Их изменение обратно пропорционально размерам (в соотношении 1/размер).

2. Коэффициенты связи между резонаторами изменяются с изменением частоты в соотношении 1/соо, но внешние добротности не зависят от частоты. Так как коэффициенты связи играют преобладающую роль при определении ширины полосы, то последняя для фильтра с ферромагнитными резонаторами остается постоянной при его перестройке (см. § 17.02), однако, форма характеристики будет изменяться. Фильтр с умеренной величиной чебышевских пульсаций в середине перекрываемого диапазона имеет большие пульсации при настройке на нижнем конце перекрываемого диапазона, и характеристика может приближаться к почти максимально плоской при настройке на верхнем .конце диапазона.

3. Коэффициенты связн прямо пропорциональны, а внешние добротности обратно пропорциональны величине М,. Таким образом, как можно видеть с учетом изложенного в § 17.02. любое изменение Ms приведет к пропорциональному изменению ширины полосы фильтра, а форма характеристики останется неизменной. Здесь нужно сделать одно замечание относительно потерь рассеяния: так как ширина полосы влияет на потери рассеяния (см. §§ 11.06 и 11.07), то по этой причине может иметь место некоторое изменение формы характеристики.

4. Поскольку внешняя добротность изменяется обратно пропорционально размерам цепи (1/размер), а коэффициенты связи изменяются в соотношении 1/шо, то получение достаточной связи между оконечными резонаторами и внешними цепями, а также между смежными резонаторами будет становиться все труднее по мере увеличения рабочей частоты. Поэтому ферромагнитные материалы с особенно большими величинами Mg должны быть полезны для применения в более высоких диапазонах.

Ко времени написания данной книги изложенные выше выводы не были систематически проверены экспериментальными сред-ствам'И; однако они, как оказалось, совпадают с имеющимися экспериментальными результатами. В частности, проведенные Картером [3, 4, 5, 6] измерения характеристик фильтров очень хорошо подтвердили второй нз изложенных выводов.

- 457 -