ввести коэффициент полезного действия по пространственным волнам

Результаты расчетов г\ в зависимости от параметров диэлектрического покрытия показали (рис. 2.55), что даже при достаточно тонких слоях подложки происходит значительное снижение КПД излучателя. Это снижение пропорционально величине е\. В связи с этим представляет интерес сравнить пзлучательную эффективность вибраторных и щелевых МПА. Пространственные волны излучаются более эффективно вибраторными антеннами при тонких подложках. Возбуждение волны LEi при определенных значениях е\ и dflQ дополнительно уменьшает значение г, для щелевых МПА, однако этот спад происходит в области d/Xo, где значение т] уже существенно меньше единицы (рис. 2.55).

0,05 0,10 0,15 d/Ko

Рис. 2.55. Зависимость КПД излучения односторонней (сплошные кривые) и двусторонней щели (штриховые кривые) от параметров диэлектрического слоя:

/ е',=2.4; 2 - 3,5; 3 - 5.0; 4 - 7,0

0,05 0,10 0,15 d/Aff

Рис. 2.56. Зависимость амплитуд по верхностных воли LM (cплoшныl кривые) и LE (штриховые), возбуж даемых щелью, от параметров диэлек трического слоя

Поведение tj для двух типов полосковых антенн станет очевидным, если сравнить амплитуды F, поверхностных волн, возбуждаемых в структуре электрическим и магнитным излучателями. Результаты расчетов амплитуд /f, для электрического вибратора приведены на рис. 2.11; для щели - на рис. 2.56. Соотношение амплитуд волн низшего типа LMi для электрического и магнитного вибраторов и соотношение амплитуд волн LEi и LM для каждого из излучателей объясняет характер зависимости Ti(rfAo). 82

2.6.3. Резонансные щели. Согласование. В большинстве микрополосковых конструкций, как открытых, так и экранированных, . используются щели резонансной длины. Резонансный размер щели определяется по обращению в нуль реактивной части проводимости: В-}-В^ + В^ = 0.

На рис. 2.57 приведены результаты численного исследования зависимости резонансной длины щели Ьрез от параметров диэлектрической подложки 8i и d. На этих же графиках штрихами приведены значения КПД щели. Следует отметить существенное укорочение щели в присутствии диэлектрика. Так, для параметров подложки, которым соответствует график рис, 2.57, это укорочение соответствует 157о для е[=2,4 и 23% для е; =5,0. Приведенные здесь данные хорошо согласуются с результатами исследования, которые были опубликованы параллельно нашей работе [58}.

Исследование резонансных свойств излучателя связывается обычно с вопросами его согласования с линией питания. Выбор резонансной длины Ьрез обеспечивает равенство нулю реактивной части проводимости. Согласование активной части G с волновой проводимостью линии питания при сосредоточенном возбуждении

V-fOCM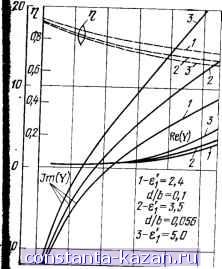

ff. Or-.-

D,Z 0,3 4 0,5 Ь/Ло Рис. 2.57.

0,f 0,2 0.3 0,fy 0.5 S/l

Рис. 2.58.

Рис. 2.57. Зависимость проводимости и КПД щели от ее длины

Рис. 2.58. Зависимость эквивалентного сопротивления щели от ее смещения относительно проводника МПЛ:

---экспериментальные результаты, ----расчет по формуле-cos (я5/о) -г г j

досТ11гается смещением точки питания от центра щели к краю. При распределенном возбуждении щели в экране МПЛ согласование достигается подбором смещения щели относительно проводника линии.

На рис. 2.58 приведены расчетные и экспериментальные значения сопротивления щели в зависимости от ее смещения от осевой линии.

Эффективность возбуждения щели, прорезанной в экране МПЛ, можно оценить с помощью коэффициента связи, определяющего долю излученной антенной мощности /С=1 - l-Sup-[-г!]- Элементы матрицы рассеяния 5 для эквивалентной схемы в впде последовательно включенной проводимости непосредственно определяются по величине Y=G+jB.

На рнс. 2.59,а, б приведены графики зависимости К от длины щели для двух значений e. Максимальное значение коэффициента достигается при относительном смещении S/b = 0,6. Уменьще-ние коэффициента связи прп меньших смещениях объясняется тем обстоятельством, что щель, будучи прорезанной под самой полоской, становится плохо согласованной, и существенная доля мощности в линии отражается. При больших смещениях щель возбуждается слабо, так как электромагнитное поле линии сосредоточено вблизи полоски. Увеличение диэлектрической проницаемости материала полоски вызывает сужение рабочего диапазона частот, для которых К не ниже заданного значения.

Полученные здесь результаты могут использоваться при проектировании синфазных АР и щелевых антенн бегущей волны, в которых заданное амплитудно-фазовое распределение обеспечивается за счет различных смещений - щелей относительно линий питания.

2.6.4. Диаграммы направленностей щелевых излучателей. Как

и в случае полосковых вибраторов, интерпретируя выражения для активных частей проводимостей как результат интегрирования вектора Умова - Пойнтинга в дальней зоне, можно непосредственно получить выражения для ДН. Ниже будут выписаны формулы

к

D,Z5 0,30 0,35 D,W D,¥5 Ь/Ло a)

К

0,3 0,2 0,1

О

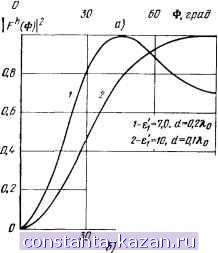
0,25 0,30 0,35 OfiO 0,15 Ь/Ко

Рис. 2 59. Коэффициент связи щели с линией:

/ S=0,5fc: 2-0,55; 3-0.6: 4-0,7; 5-0.8; 6-0,9 84

для диаграмм при одномодовой аппроксимации поля в щели. Более общие результаты для этой характеристики щелевой МПА можно \ получить на основе обращения матрицы частичных проводимостей способом, описанным в 2.6.2.

Диаграммы направленности поверхностных волн:

cosФcos(ko(bj2) V&[ - (а^)2 sinФ)

sin Ф cos(kob/2-ye[- (a(;)2sin Ф)

1-(Ао6/7г./Е;-(а^,25шФ)

где угол Ф отсчитывается в плоскости yoz от оси z (см. рис. 2.52).

Волны различных типов и номеров возбуждаются с различными амплитудами, значения которых определяются по графикам рис. 2.56. Это обстоятельство необходимо учитывать при построении общей картины распределения электромагнитного поля в диэлектрике в случае многомодовых структур.

На рис. 2.60 приведены графики ДН поверхностных волн LMi и LEi. Диаграмма волны LMi сохраняет однолепестковый характер в довольно широком диапазоне изменения е[ и d/Ko. Излучение волны LE] при повышенных значениях е[ и d/}.o носит коле-.бательный характер. Выражение для ДН пространственных волн !в произвольном сечении левого полупространства (рис. 2.61) опре-1дёляется из выражения для G, (2.55). Для главных плоскостей запись упрощается:

в плоскости вектора Е (ф = 0)

F(b) = sin е (е; sin е cosT,MP+(r, sinl.M);

в плоскости вектора Н (е=я/2) f cos (fepfe sin <р/2) , cos<p

(2.56)

(2.57)

1 -{kobsinlk) K(coscpsin?,M) + (4osl,M) В (2.56) - (2.57) e, ф являются углами сферической системы оординат.

Расчетные графики ДН по мощности для главных плоскостей приведены на рис. 2.61, из которых видно, что диаграмма в плоскости Е более чувствительна к изменениям параметров подложки, 1ем в плоскости Я. При d-0 из (2.56), (2.57) следуют известные Ьормулы для диаграммы направленности щели в металлическом *>кране.

2.6.5. Щель в экранированной МПЛ. Недостатком рассмотрен-юй в предыдущем разделе МПА является двустороннее излуче-Ьие щели. Для создания однонаправленной антенны на основе Ьелевого микрополоскового излучателя используется дополни-1-ельный экран со стороны диэлектрического покрытия (рис. 2.62) шли в качестве линии питания используется экранированная ПЛ. С точки зрения электродинамики такая система имеет бо-ее простое описание, так как в неоднородной области (справа

.o,.z

0,8 0.6

60 Ф. граВ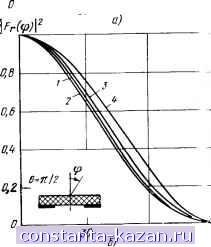

60 (г!,гра-

Рис. 2.60. Рис. 2.61.

Рис. 2.60. Диаграммы иаправленности поверхностных волн щелевого излучателя. а) волны LMi; б) волны LEi

Рис. 2.61. Диаграммы направленности пространственных волн щелевого излуча теля в главных плоскостях:

/-d=0,05/,o, ei=2,4; 2-е',=2,4, d=G,\%o\ 3 -ei=3,5, d=0,\%o\ 4 -e,=5,0. d=0,l Xo

ОТ щели на рис. 2.62) содержится лишь дискретный спектр волн, распространяющихся в плоскопараллельном волноводе, а слева от щели спектр волн только непрерывный. Внешняя проводимость определяется в этом случае как проводимость излучения односторонней щели в плоском металлическом экране [95]. Остановимся на расчете внутренней проводимости щели. Ее-величина определяется стандартным функционалом:

(2.58)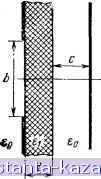

Входящая в (2.58) компонента тензорной функции Грина магнитного типа для исследуемой области состоит из двух членов: первый соответствует счетному набору поверхностных волн, прилипающих при распространении к границе раздела воздух - диэлектрик, второй - бесконечному ряду осциллирующих типов колебаний, т. е.

Г

22; уу ~ mi

171=1

В соответствии с таким представлением функционала (2.58) проводимость щели складывается из нескольких слагаемых, имеющих четкий физический смысл:

(2.59)

Рис. 2.62. Щель в экране со слоем диэлектрика с дополнительным проводящим экраном

Вычисления слагаемых формулы (2.59) нетрудно сделать, используя записи собственных функций поверхностных и осциллирующих волн, приведенные в § 1.4 (случай 1).

%0 ..... ,

0,30

0,20

0,20

0,10

С/Ь

Рис. 2.63. Рис. 2.64.

Рис. 2.63. Зависимость проводимости резонансной щели от высоты подвеса дополнительного экрана:

/ -е,=2,4; 2 - 5,0; 3 - 7,0; -d=0,106;----d=0,056

Рис. 2.64. Влияние высоты подвеса дополнительного экрана на резонансную длину щели:

в=0,0566; / -ei=2,4, d=0,056; 2 -ei=2,4, d=0,l 6; 3 -ei=5,0, d=0,056; 4 -ei=5,0, d=0,16; 5 -ei = 7,0, d=0,05 6; 5-e,=7,0, d=0,l 6