На рис. 2.63 показаны зависимости проводимостей резонансных щелей в плоскопараллельном волноводе с диэлектрическим слоем для двух значений толщины подложки и трех значений ее диэлектрической проницаемости. Так как толщина слоя достаточно мала, то приближение к нему дополнительного экрана вызывает существенное увеличение проводимости щели. При увеличении d/b зависимость становится менее крутой. Следует заметить, что уменьщение расстояния от экрана до поверхности диэлектрика (с/Ь) вызывает заметное снижение излучательной способности щелевой МПА (рис. 2.64). Аналогичное явление отмечено в [59] для полого плоскопараллельного волновода. Увеличение толщины слоя и уменьщение его диэлектрической проницаемости способствует меньшему изменению Ьрез/Ао прп

Изменением геометрических параметров антенны можно регулировать долю мощности, излученной щелью. В табл. 2.3 для нескольких разновидностей устройства приведены коэффициенты

а = Re (У)/Re (У), характе-у См 10 ризующие соотношение мо-

~ ~ щностей, излученных щелью во внешнюю область и внутрь волновода.

Для иллюстрации резонансных свойств щели, прорезанной в экране МПЛ, на рис. 2.65 приведены зависимости полной проводимости

щели У=У--У для шести типов подложек. Естественна прямая зависимость резонансной длины отверстия от Еу Удаление экрана и увеличение толщины подложки вызывает незначительное увеличение Ьрез.

Дальнейшее повышение степени экранирования внутреннего объема щелевого излучателя приводит к ре-зонаторно-щелевой конст-Таблица 2.3

-г

о л

Рис. 2.65. Зависимость проводимости щели с дополнительным экраном от ее длины: а=0,05 6; d=0,l 6; / -ei=5,0, с=0,16; 2 -е',==5,0 с=0,2 6; 3 -ei=2,4, с=0,2б; 4 -е',=2,4, с=0,16

рукцин. Теорегический анализ такой модификации щелевой антенны ие вызывает сложностей, так как и в случае конструкции рис. 2.62 решение самой трудоемкой части задачи - определение внешних проводимостей излучений здесь не представляет трудностей и, как было отмечено, сводится к определению характеристик щели в проводящем экране. Как показывает анализ расчетных и экспериментальных результатов, приведенных в [60], резо-наторно-щелевая антенна на базе МПЛ не имеет существенных преимуществ перед антеннами, выполненными на полых резонаторах с диэлектрическим заполнением ни по электрическим, ни по массогабаритным характеристикам.

ГЛАВА 3.

ДВУМЕРНЫЕ ПОЛОСКОВЫЕ ИЗЛУЧАТЕЛИ

3.1. ОПРЕДЕЛЕНИЯ. МЕТОДЫ РАСЧЕТА

Основные успехи в практическом использовании МПА связаны с плоскими двумерными конструкциями. Это - излучатели в виде металлических структур правильной или неправильной геометрической формы, расположенных над слоем диэлектрика с металлическим экраном (см. рис. В. 1,6-к).

Возбуждение таких антенн осуществляется от коаксиальной или полосковых линий (рис. 3.1). Во втором случае конструкция получается весьма компактной, к тому же на антенной плате возможно размещение элементов управления излучением или схем бработки сигналов.

Первые сообщения об антеннах рассматриваемого типа относятся к 60-м годам. Однако их практическое использование и назло всестороннего исследования характеристик связывается с менем Мунсона [63]. К настоящему времени известно несколько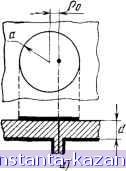

Рис. 3.1. Возбуждение МПА:

а) от коаксиальной линии; б) от МПЛ

методов расчета антенн этого класса. Остановимся на некоторых из них.

Простейший подход к анализу наиболее распространенной прямоугольной конструкции МПА основан на использовании теории длинных линий [63]. Отрезок открытой МПЛ шириной а и длиной b (см. рис. 3.1,6) полагается наруженным с обеих концов излучающими щелями. Каждая кромка длиной а отождествляется с узкой щелью, излучающей в полупространство, ограниченное металлическим экраном, проводимость которой определяется с помощью (2.45):

Ух = G, = ш/К Уч/\о [1 + У (1 - 0,276 In М)]. (3.1)

где d - ширина щели, равная приблизительно толщине подложки.

Выражение для проводимости щели без жестких ограничений на ее относительную ширину получены также в [102, с. 188]:

-у

J Jo(x)dx - Л (kod)

Yi=ald-Vo

Л^о (jc) dx + {k,d) + 2/irfeed

где J {x), А^ (л:) -функции Бесселя и Неймана порядка п. Для малых d/ko следует выражение, аналогичное (3.1):

Гц = Vol 1 + / (1 -0.636In М)].

Для того чтобы вторая щель излучала поле синфазно с первой, длина резонатора берется несколько меньше Х/2, где = \/V]{e-i=eJeQ). Укорочение резонатора до значения (0,49- -0,48) Я связано с наличием реактивной энергии, запасенной вблизи кромок. Проводимость второй щели пересчитывается к первой кромке как Y2=Y*=Gi-jBi, в результате чего входная проводимость резонатора определяется как сумма проводнмостей концевых щелей:

Ув = (G, + у5,) + {G, -f jB) = 2G,.

Например, для щели длиной ко Gi = 0,00834 1/Ом и /?вх = = 1/2 Gi=60 Ом.

Резонансная частота aHTenjibi определяется с учетом укорочения как /o=c/[(0,96-0,98)b/ e;j.

Большое распространение получил резонаторный метод, позволяющий исследовать характеристики МПА правильной геометрической формы- [6, 64]. При этом поле между металлической пластиной и экраном разлагается по собственным функциям электромагнитного резонатора соответствующей формы с магнитными стенками. Эффект излучения учитывают введением эквивалентных потерь или путем использования граничных условий импедансного типа на стенках резонатора [64]. Соответствующие проводимости 90

излучения определяются (3.1) или по формуле, учитывающей реактивную часть проводимости, как в случае открытого конца МПЛ 165] (ср. [1])

V = 1га/37бХо + jO.OOmSbaeldXo, (3.2)

где

Вэф-О.З

, a/d+0,262 Л./ = 0,412 3,3 .

эф = 0,5 (е; + 1) -f 0.5 (е; - 1) (1 ч-10с?/а)-/2.

(3.3)

Оба подхода лишь косвенно учитывают влияние диэлектрической структуры при определении параметров излучения, что не позволяет с необходимой точностью определить некоторые важные характеристики антенны: рабочую полосу, КПД.

Другая группа методов - это точные по постановке подходы, сводящие соответствующую электродинамическую задачу к векторному интегральному уравнению относительно токов на металлических частях МПА, которое решается одним из вариационных методов [9, 74-76, 105]. Теоретические результаты на основе этих подходов немногочисленны и получены ценой весьма больших затрат машинного времени. В большинстве случаев результаты решения граничной задачи не могут быть непосредственно использо Ваны для определения всех необходимых характеристик расчетной подели как антенны.

В настоящей главе излагается метод определения характеристик МПА, основанный на электродинамическом подходе, рационально сочетающий преимущества токового и резонаторного методов. Предлагаемый подход учитывает конструкторско-техноло-гические параметры устройства, потери в диэлектрике и металле, количественные соотношения между мощностями, переносимыми поверхностными и пространственными волнами, более строгий расчет внешних проводнмостей и сопротивлений излучения, поляризационных потерь, взаимодействия излучателей и др. Возможность учета многомодового характера полей в МПА и окружающей структуре, содержащей диэлектрик, и строгий учет вклада поверхностных волн позволяют использовать предложенную методику расчета МПА вплоть до волн миллиметрового и субмиллиметрового диапазонов.

3.2. ПРЯМОУГОЛЬНЫЕ МПЛ

3.2.1. Модифицированный резонаторный метод. Прямоугольная МПА, возбуждаемая от коаксиальной линии, изображена на рис. 3.2. Для анализа характеристик такой антенны воспользуемся уточненным резонаторным методом. Его уточнение - модификация- связана как с внутренней, так и с внешней частью соответствующей граничной задачи. Внутренняя - резонаторная задача решается в два этапа. На первом - определяются электромаг-

нитные поля в прямоугольном резонаторе с магнитными {х = 0,о; у = 0,Ь) и электрическими (2=0, d) стенками. Для резонаторов, когда d<CAo, распределение электрического тока на возбуждающем штыре близко к постоянному и поле внутри резонатора является суперпозицией колебаний типа E q. В этом случае продольная составляющая электрического поля

о оо

А = -JH 2 2 - / ifmjkiin) COS (Tmuola) cos {т.пЬо1Ь)Х

m=0n=0

X COS {nmxja) cos (глу/Ь),

(3.4)

где

imn = УЩ - kl, = Vmjaf - (Ш1Ь)\ k, = ko Ve[.

Составляющая в (3.4) получена интегрированием функции Грина Гц с характеристической частью, связанной с осью z. Более удобным является представление для Е^, когда используется соответствующая компонента функции Грина с характеристической частью, связанной с осью у. В этом случае

/ l/-- У - cos{mia,:a) X

X cos (j:mxja)

cos(T y) cos u{b-bo) cos (ubo) cos {b - y)

y<bo, У > *o.

(3.5)

где

T ,= Kft?-( / )-

Ha втором этапе напряженность электрического поля Е^ используется для определения эквивалентных магнитных токов на всех или только синфазно-излучающих стенках резонатора. В этом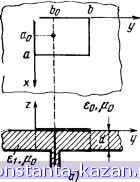

Рис. 3.2. Прямоугольная МПА и соответствующий ей резонатор с эквивалентными электрическими и магнитными токами: а) конструкция; б) распределение токов 92

случае стенки полагаются электрическими, и эквивалентный магнитный ток

J =nXE, (3.6)

где п - внешняя нормаль к стенке.

Далее решается задача определения входного сопротивления резонатора, возбуждаемого электрическим током и излучающего через боковые отверстия.

Во внешней области улучшение метода связано с более корректным определением проводимостей излучающих токов в при-Сутствии диэлектрического слоя и с учетом возбуждения как про- странственных, так и поверхностных волн.

Используем указанные выше особенности резонаторного метода при анализе характеристик прямоугольной МПА, функционирующей в режиме низшего типа колебаний.

3.2.2 Входное сопротивление прямоугольной МПА. Полное входное сопротивление антенны Zbx является одной из основных ее характеристик. По частотному графику Zbx можно определить согласование антенны с линией питания, рабочую полосу, доб-ютность.

Определим входное сопротивление МПА прямоугольной формы, функционирующей вблизи первого резонанса (наибольшая рабочая длина волны). Внутреннюю область антенны можно рас- :матривать как объемный резонатор, заполненный диэлектриком, а рис. 3.2,6 показаны эпюры и направления эквивалентных то-ов на открытых стенках резонатора. Токи на торцевых стенках (y=0,fc) в этом случае синфазны и формируют основные компо-енты поля излучения, в то время как токи на боковых стенках (л; = 0,а) содержат противофазные участки и слабо участвуют в излучении. Это излучение формирует кроссполяризационную составляющую поля во внешней области. Расход энергии на образование этого излучения будет учтен в дальнейшем при определе-ии добротности, рабочей полосы и КПД антенны. В этих условиях ходиое сопротивление антенны, возбуждаемой сторонним элек-рическим током J, определяется для резонатора с магнитными боковыми стенками и электрическими торцевыми стенками, на которые накладываются вторичные поверхностные магнитные токи 1Г. Ч-

Эти токи берутся из решения вспомогательной задачи в соответствии с формулой (3.6).

Введенная таким образом система токов имеет следующую запись:

= /ой {X - Хо) 8 (у - Уо) а„ J -= l/i8 (у - 0) У, {х) а,.

l- = Vb{y-b)JMa,. (3.7)

В соответствии с (3.5) и (3.6) для функции распределения магнитных токов имеем: