A, ft \2 K/2

sin (0,5oa sin G cos f)

0,5koa sin e cos 9 (? cos e sin tp)

cos (0,5 sin 0 cos tpftjfe)] . l - (kobl-) sin 6 sin cp J I 4- (£, cos 6 ctglftorf) (cos 6 cos sp)-

COs2e + (TctgSM)2

sin Ode d-s.

(3.43)

Индекс п означает, что сопротивление отнесено к току в пучности, в данном случае -к току в центре пластины. Это сопротивление антенны может быть пересчитано на край пластины (точка возбуждения прямоугольной МПА) по формуле четвертьволнового трансформатора:

вх = 2Ж + да. (3.44)

где Zc - характеристическое сопротивление эквивалентной открытой полосковои линии шириной а.

Для сравнительно широких линий Zc rf/o]/fio/Ei.

При подстановке Zc к R ъ (3.44) и с учетом того, что вблизи резонанса антенны А;оЬ/я 1/У , /?вх=1/С', где

а sin (OMoCi sin е cos 9)]2 [ cos (0,5*0 sin 6 sin 9) ч 2

4 >/2 0

0,5*0 sin b cos <p

1 - (kobjtz sin 6 sin <fY

(Tcos6 sin <p)2

(cos G cos p)2

-jsinerfedcp. (3.45)

+ (ei cos e ctglM) cos2 e -i- (-ctg ikdf

Величина G имеет смысл проводимости излучения двух торцевых отверстий длиной а, разнесенных на расстояние Ь.

Резонаторный метод для суммарной проводимости дает сходное выражение <см. 3.2.3):

/2 Г а sin (0,5/еоа sin 6 cos

ly ]}[2 0,5*оа sin 6 cos ср

.rruu . п м) (Т cos 6 sin ср)2 ,

X [ cos {0,5k,b sin е sin ср)] ~--т-. +

ir2+(E;cos6ctg?M)

(cos е cos <р)2

sin bdbdf.

(3.46)

cos2e+(TctglM)

Диаграмма направленности двух отверстий, разнесенных на расстояние Ь, с учетом (3.46) имеет следующий вид: в плоскости Я (ф=0)

F,{b)

2 cose

1со82е + (rctg?V)

sin (0,5*оа sin 6) 0,5*o sin 6

(3.47)

Б п Л о с К о с т И £ (ф=.-1/2)

2 cos е cos (0,5*0 sin G)

Fb (G) -

(3.48)

2+(eJcos GctgMj Амплитудная ДН металлической полосы, определяемая непосредственно из (3.43), рассчитывается по формулам: в плоскости Н

]/COs2e l-(Sctg?*o)2

в п,чоскости£

2FcosG

sin (0,5*oasin 6) 0,5*оа sin е

lT-f(e; cose ctg V)

cos {0,5kob sin 6

\-(klt. sin 6)2

(3.49) (3.50)

Формулы (3.47) и (3.49) для расчета ДН в плоскости Н совпадают. Иден-гичность выражений (3.48) и (3.50) легко устанавливается для частот вблизи зонанса следующим очевидным преобразованием:

1 А

1 - (kbj- sin 6)2 1 - ( sin 6/ у, е| )2 s; - sin2 fj f2

По формуле (3.44) произведен расчет входного сопротивления прямоуголь-1ЫХ Ь\иХ с целью исследования зависимости резонансной частоты н резонанс-юго сопротивления МПА от ее размеров. На рис. 3.11,о приведена серия графи-юв R п X для нескольких значений ширины металлической полосы.

т ш

WD W

о

гоо

Рис. 3.11. Частотные графики активной и реактивной частей входного сопротивления прямоугольной МПА, возбуждаемой у кромки:

/ - 0/6 = 1,0; 2-1,2; 3 - 1.4; 4-1.6 (о); зависимость резонансной частоты прямоугольной МПА от ее размеров (б)

D,if6 07 0,16

а) й/с^.Ао

3,0 hb 107

3.2.6. Выбор размеров прямоугольного излучателя в соответствии с теорией краевых эффектовЭлектродинамические характеристики МПА в рамках описанного выше резонаторного метода (см. также [1]) можно установить, используя концепцию парциальных волн. Основой для проведенных в этом разделе расчетов служит строгая теория учета краевых эффектов, развитая для МП направляющих структур в [1]. При анализе используется амплитуда и фаза коэффициента отражения, который представим в виде функции T=T{kodYi, Ф). где Ф -угол падения плоской Т-волны на кромку ключевой структуры, образованной металлической полуплоскостью, лежащей на поверхности плоскопараллельного фольгированного с обратной стороны диэлектрического слоя Аппроксимация краевых полей реальных структур полями, возникающими при падении плоской волны на такую полубесконечную структуру, позволяет выделить соответствующие граничные условия и свести задачу к рассмотрению двух задач: внутренней н внешней. Излучаемая и реактивная (запасаемая во внешней области резонатора) мощности описываются при этом через полную проводимость стенок резонансной полости, а граничные условия, в силу единственности решений, обеспечивают непрерывность внутренних и внешних полей. Такой подход приводит к системе трансцендентных уравнений поперечного резонанса, определяющих важ нейшие электродинамические характеристики излучателя (резонансную частоту, добротность, проводимость излучения, КПД по пространственным волнам и т. д.).

Проиллюстрируем сказанное на примере резонансной частота прямоугольного МП излучателя. Его комплексная резонансная угловая частота co = co-l-/Q в режиме свободных ТМ , колебаний определяется так:

2ш2е,1Хо= УГ+ 2Q2e,H. = Vj- g,

f = (PL + Kn)+( L++2 [( ..Р.. + ynW -

& xm I ryn xm jrn*

где kjc, Ay, компоненты комплексного волнового числа пар циальной волны в направлении х и у осей соответственно. Знач(. ния jr, т„ и ky, находятся из рещения системы уравнений п( перечного резонанса и определяются исходными размерами а, Ь i d излучателя (рис. 3.2) и относительной диэлектрической пронп цаемостью подложки. Распространение парциальных волн в резонансной полости происходит таким образом, что углы падения и\ на каждую из кромок элемента принимают значения, при которых

Этот раздел написан авторами по материалам Е. К. Конина. Ему же пр. надлежат приведенные численные результаты.

ективные плоскости отражения ( магнитные стенки) ока-Шваются на расстояниях тя/(2Рд. ) и ля/(2Ру ) от центра эле-кента в х и у направлениях соответственно. Этим определяется исло вариаций и структура поля вдоль каждого из двух взаимно ртогональных направлений. Так, для основной ТМю волны, для ыполнения условий поперечного резонанса, отражение от краев = const должно иметь индуктивный характер, а при падении или на края A;=const - емкостной. При этом эффективные пло-кости отражения от первых проходят через центр излучателя. С зменением размеров элемента его резонансная частота изменяет-я, но мы остановимся лишь на практически интересном вопросе i6 изменении размеров а и b излучателя при сохранении его ре-онансной частоты. С увеличением ширины а, для удержания ффективной плоскости отражения на оси симметрии излучателя, гол падения парциальных волн на края y=const должен увели-иться, усиливая тем самым индуктивный характер отражения I электрически компенсируя вызванное увеличение ширины эле-1ента. Это влечет за собой равное уменьшение углов падения на злучающие края л; = const, усиление емкостного характера отра-<ения от них и уменьшение соответствующей резонансной длины. )днако изменение размеров происходит неодинаково. При боль-цих углах падения их малые возмущения вызывают значительные двиги эффективной плоскости отражения. Наоборот, при малых глах падения их изменения ведут к сравнительно малым смеще-иям этой плоскости. Поэтому в режиме низкодобротных ТМю олебаний даже существенное увеличение ширины МП прямо-гольного излучателя требует малых изменений углов падения на се его четыре стороны. При этом соответствующие изменения езонансной длины элемента оказываются небольшими. На ис. 3.11,6 представлены вычисленные резонансные размеры пря-[оугольного МП излучателя. В качестве параметра принята нор-шрованная толщина kd. Из приведенных результатов следует, что юльшому интервалу возможных значений нормированной шири-ы ka в низкодобротном режиме колебаний отвечает лишь небольшой участок значений соответствующей нормированной резонанс-юи длины kb элемента, причем последняя не может быть меньше 1екоторой определенной величины, зависящей от толщины kd шэлектрика. При уменьшении ka излучательная способность элемента падает, а добротность увеличивается. Начиная со значений и меньших, с уменьшением ka добротность быстро растет и элемент начинает функционировать скорее как резонатор, нежели <ак антенна.

3.2.7. Диаграмма направленности прямоугольной МПА. Поля-)изационная характеристика. При элементарном подходе ДН пря-лоугольной МПА в плоскости Н эквивалентна диаграмме щели длиной а, прорезанной в плоском проводящем экране и имеющей авномерное распределение поля. В плоскости Е излучение МПА определяется как излучение двух таких щелей, разнесенных на ширину резонатора Ь. При таком подходе влияние подстилающего

диэлектрического слоя не принимают во внимание. В некоторых работах (см., например, [12]) это влияние^ учитывается введением дополнительного множителя cos(ftoC? ]/£ cos 6), учитывающего зеркальное изображение магнитного тока в экране.

Более корректное интегрирование распределения электрического поля (магнитного тока) по апертуре излучающих торцов МПА приводит к формулам § 2.5 в связи с рассмотрением излучения кромок полосковых структур и в предыдущем пункте в связи со сравнением апертурного и токового методов расчета характеристик МПА [см. (3.47) и (3.48)].

На рис. 3.12 приведены расчетные ДН прямоугольной МПА в плоскости Н F(Q) и плоскости Е fe(6). Следует обратить внимание на спад составляющей Еь при углах, близких к 90°. При

элементарном рассмотрении излучения этого явления установить не удается. Строгое решение соответствующей задачи методом интегрального уравнения также устанавливает отмеченный спад интенсивности излучения (см. 3.3.2).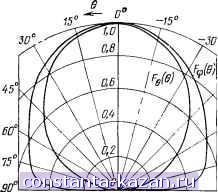

-60 Рис. 3.12. Диаграмма направленности прямоугольной МПА в главных плоскостях:

-90

е',=2,3; Ь Г е', = 0,4927 Хо; rf .o=-= 0,006836; a=b

Приведем расчетные формулы для ДН прямоугольной МПА, пригодные для произвольной плоскости, которая проходит чере. ось г:

cos е cos у ехр Uribl2) Kcose + dctglM)

-\- (kod) cos 6 cos <p exp (-fib/2)\,

cos 6 sin <p exp Uribl2)

(3.51

Fb{b, <p) = M,{b, <p)

.V r2 + (e;cosectglV) X -~ + {kod) sin <p exp (- /ribl2)

где Mi(0, ф) рассчитывается по (3.25).

Еще на один момент следует обратить внимание в связи с рассмотрением полей излучения МПА. Боковые стороны прямоугольной МПА хотя и содержат противофазные участки тока, существенно ослабляющие излучение в направлениях, близких к норма-

ли, все-таки они служат источником кроссполяризационных со-. ставляющих поля излучения. Пространственное распределение поля в дальней зоне от этих токов

f;(e, ср)=Жз(е, ср)

cos 6 sin у ехр (-ySa/2)

Kcos2 6-f.(lctglM) - {kgd) cos e sin у exp (-/ca/2)];

cos e cos у exp Ulal2)

(3.52)

Fl(b, у) = Жз(е. у)

V + {b\ cose ctg

X -jr- -{kod) cosy exp (- }Ы, 2)

где Л1з(6, ф) дается выражением (3.26).

Перейдем к рассмотрению поляризационной структуры поля, 13лучаемого МПА. Составляющие поля, связанные с единичными лекторами сферической системы координат и а^, не определяют главную Егл и паразитную Еп составляющие поля излучения антенны. Для МПА, изображенной на рис. 3.2,а, система координат, в которой £гл и Еп соответствуют единичным векторам орто-нальной системы а;-, ag-, а~, угол 6 отсчитывается от оси у, угол ф -в плоскости XOZ от оси Z в сторону оси X. Во введенной таким образом системе координат a = a, ап = а~.

Единичные векторы двух названных систем координат связаны между собой соотношениями [103]:

а^ = -[1 - (sinO sin y)-] [cos уае -cosO sin ya. ],

a~ = - [1 - (sin 6 sin y)2]-i/2 [cos 6 sin yae + cos ya,p].

Главная и паразитная составляющие напряженности электрического поля определяются в этом случае как

а^>. £ = <£, а~>, (3.52а)

где

Е(е, у) = £е(е, у)ае + £,Ле, ?)а^.

Скобки в (3.52,а) означают скалярное произведение векторов.

Под поляризационной характеристикой антенны будем попинать комплексную величину

r(fj, у) = (6, у)/£ (е, у)= ! г (6, у) I ехр[/Ф(е, у)]. (3.526)

Модуль и фаза г (9, ф) могут быть непосредственно использо-аны для определения параметров поляризационного эллипса

Определим в рамках резонаторного метода вклад ортогональных составляющих токов (J и на рис. 3.2,6) в поляризационную характеристику антенны. Полагая, что излучающими являют-