Векторные потенциалы А', А^ электрического и магнитного Это -волны Е относительно координаты х или волны LM [51]. токов j являются решением уравнений Гельмгольца: Положив A = ait-, можно записать поля для волн типа LE.

дА + ;2дэ. м 1э, м (I 2 Следует заметить, что функции ¥ в (1.5) и (1.7) являются ре-

шением уравнения Гельмгольца и должны удовлетворять в общем Рассмотрим несколько частных случаев выбора потенциалов случае различным граничным условиям. Например, в случае пря-Пусть Л = 0 и моугольного волновода с поперечными размерами а п b имеем:

А* = а^!-, (1.3 i-e = sin (tmxja) sin (rnylb) ехр (-Утт г),

Тог^ единичный вектор. ц-н^ cos {тх/а) cos (ny/b) ехр (- угт 2),

1 Vn = (r.mxia) sin (тгпу/б) ехр (- h, nZ),

Е = уЪаА + -- V (V - Д^). Н = V X A (1.4 v-le = rnxa) cos {.nylb) ехр (- /Y. ).

что позволяет выписать скалярные компоненты полей в прямо т-0, 1, 2, ... , м-0, 1, 2, ... ,

угольной системе координат: = У k - {r:miaf - {ш/Ьу.

1 d-W dW Система волн, аналогичная рассмотренной, может быть полу-

~Мд ~д^ ченадляа = а,.

Е я п 5 МЕТОД ТЕНЗОРНОЙ ФУНКЦИИ ГРИНА В ЗАДАЧАХ

/сое дудг * ЭЛЕКТРОМАГНИТНОГО ВОЗБУЖДЕНИЯ

/сое

*2 1 \ хгЕ и п Широкий класс задач возбуждения сводится к решению неод-

~г г = и. породных векторных уравнений (1.2) с последующим вычислением

полей Е и Н по (1.1). Правая часть уравнений типа (1.2) содер-Электромагнитные поля, не содержащие компоненты Н^, на- жит физически существующие или эквивалентные токи. Одним из зываются поперечно-магнитными или типа Е. распространенных способов отыскания Е и Н по заданным и

Положив А^ -О и A = aF , легко из (1.1) получить выра / является метод функции Грпна, который широко используется ження для составляющих электромагнитных полей, аналогичны.х при решении скалярных задач. В этом случае функция Грина (1.5), где£ =0. Это - поперечно-электрические пли'волны типа Н является решением дифференциального уравнения при точечном В однородной области, свободной от источников, произвольные возбуждении. Если она известна, то нетрудно найти решение при электромагнитные поля могут быть представлены в виде суперпо- любом заданном распределении источников. Например, если из-зиции волн типов Е и Н. вестей потенциал точечного заряда G(r, г'), где г - точка наблю-

Так как направление г произвольное, то дения, г' - точка источника, то потенциал и заданного распреде-

дэ ШЕ Ам ления зарядов плотностью р(г') определяется как суперпозиция

а* . А -aw , (1-6) потенциалов точечных зарядов путем интегрирования по объему:

где а -постоянный единичный вектор. / ч Г г/ м г

Для дальнейших приложений представляет интерес выбор еди- и(г) - ] и (г, г )р(г) av .

личного вектора а = а^.

В этом случае вместо (1.5) имеем Определение потенциала - скалярная задача и функция Грина

. / здесь скалярная. В задаче определения электромагнитных полей,

=-{k+ I W, fi =0 е- в векторной задаче, функция Грина -объект более сложный,

/сие \ дх) x > gj вектор. Действительно, простейшим источником в электроди-

.. , намике является точечный заряд и диполь, не имеющие направ-

Е - о у , ление. Чтобы, например, в декартовой системе координат охва-

/сое дхду dz 1ть все возможные случаи, следует найти по три составляющих

2.тг поля л:-го, у-го, z-ro диполей. Таким образом, поле Е связано с

Е = f-f источником - диполем, обладающим моментом II, соотношением

/сое дхдг ду Е = [Г]Л, (1.8)

г г г

Г Г Г

ух уу yz

гх \\у

где [Г] образует таблицу (матрицу) из девяти элементов- В [28, 30] наряду с матричным применяется так называемое

1иадное представление функции [Г]. В этом случае тензор Г (оез кобок) записывается в следующем виде:

Подобные объекты, следующие по сложиост[1 за векторам! + Г^уЭа + Г^гадга^ +1 vy + a,a.

называются тензорами второго ранга [27J. еде а.а^ -так называемое дпадное произведение единичных век-

В записи (1.9) Vij есть t-я компонента поля Е, обусловленнагоров'(в отличие от скалярного илп векторного произведения век-/-направленным элементом электрического тока. Вектор Е можеторов точка или крестик между множителями не ставится), быть полем свободного пространства, в этом случае [Г] называете В дальнейшем будем пользоваться скалярным произведением функцией Грина свободного пространства. В другом случае Е модиад на вектор. Следует различать умножение диады на вектор жет быть полем источника Л в присутствии некоторого металлг справа и слева . Например:

ческого или диэлектрического тела в свободном пространстве ил /о о . я я - я я (я а 1 - О

в замкнутой области. В этом случае строится функция Грина (а^а^)а^, - а^а^-а^ - а ЛуКлл^) и,

этой области, удовлетворяющая определенным условиям на гра а^(а^а^,) = а^-а^а^, = ау, (а,ау)а^, = 0.

Скалярные компоненты функции Грина [Г] могут быть опреде Выражение (1.11) можно теперь переписать в виде лены для свободного пространства, возбуждаемого, например ¥ it- г'\ \ tr\ HV

электрическим током, ориентированным в направлении оси х I Е(г)= \ 1. rrJ

этом случае единственная составляющая векторного потенциал

Л =/Uxvi~ik I г-г' I 1/4 I г-г' I /I If Де точка означает произведение диадной функции Грина на век-

Р1 I I I г г . тор скалярно справа.

Сопоставив (1.8) и (1.7), получим* Решение задачи возбуждения как электрическими, так и маг-

нитными токами приводит к необходимости введения четырех тен-(k \ цг зорных функций Грина:

- E(r) = jlf (r.r)-f(r) + ?i2(r.rrf(rO]V ,

У^ H(r) = j[r,.(r.r)-J4r)+r,3(r,r)-r(r01rfV. 0-12)

xx--:-

Р 1 дч-

ух -

р 1 2ЦГ 1

где dzdx Воспользовавшись векторным аналогом формулы Грина [28],

,тг , ., . можно получить полезные соотношения симметрии для тензоров:

¥=ехр{-/г-г'}/47г|г-г'. s

преобразований инозаписатьТобдам виде Pi Г„ (г, г') = - Г„ (г', г). (1.13)

I / 2 \ где знак ~ означает операцию транспонирования.

iii = -.- k-\--;- W, Г,..= -i ф f Формально полное описание полей при произвольных источнн-

\ didi J - ytue r=J ках в форме (1.12) требует знания 36 скалярных компонентов

Определенная таким образом (Ьункпн Гп о Функций Грина. Однако использование свойств симметрии (I.I3)

зоваться для вычисления няпп -> Ц * рина может исполь- и принципа двойственности электромагнитных полей сокращает

от произвольно ориентированног!ГТ п7р' - Р веского поля Е число необходимых скалярных компонентов до 15.

электрического тока j(r)- Распределенного в объеме V Остановимся на методах определения тензорной функции Гри-

на. Следует заметить, что в замкнутой форме функции Г (г, г')

E(r) = J [Г(г, г')] f (r)dV (] могут быть получены для закрытых и открытых областей с гра-

V \, Вицами, являющимися ifacTbra координатных поверхностей соот-

2 ,3

ветствующих систем координат. В прямоугольной системе с сдн(;лассифицируются типы волн для однородных областей в прямо-родным заполнением векторные уравнения для потенциалов тЪльной системе координат, не играет существенной роли, так разделяются на три независимых скалярных, которые решаютс-ак в этом случае все оси координатной системы равноценны. В стандартными методами. В случае неоднородного заполнения ил)тих условиях наиболее удобным является комбинированное пред-непрямоугольной системы координат решение векторных задатавление тензоров Грина: разложение типа Фурье в поперечном усложняется. Для нахождения функций, аналогичных Ч^(г, ri-ечении области и представление бегущими или стоячими волна-необходимо решать уравнения тензорного типа вдоль оси, связанной с вектором а. Эта последняя часть функ-= щи Грина связывается с решением Даламбера [29] и называется v-G - (r г')4-20- (г г']=-ЕЬ(г г') П исарактеристической или истокообразной. В случае, когда область * (аполнена слоистым диэлектриком (границы раздела соответству-где £ -единичный тензор; б (г, г')-трехмерная дельта-функцияот координатным поверхностям), выбор координаты, относитель-пространства решение было фактически пол) ю которой строится характеристическая часть функции Грина, чено в § 1. : 1риводит к существенно различным записям тензоров Г (г, г'). / / / ехв i- ik г - г' \ \ Рассмотрим слоистую структуру, g(r.r)=G-(r.rO = (a,a, + a,a,-f а,а,) Р^ \ П . да ось z перпендикулярна гра-

47Г I г -г I jjgg раздела слоев, не ограничен-

Тензорные функции? связаны с и G дифференциальными^ плоскости хоу (рис. 1.1). Вы-операторами, которые устанавливают связь мeжJ/эLк?SгГт-°P Р' = приводит к разными полями и векторными потенциалами [см. (1.1)1 Напоимео o* тензоров Г по волнам ти-

тов Е и Н. Поперечное сечение об-

Г,2(г г') = -V У О^Чг г'1 является однородным и неод-

юродность среды будет учитывать-

Для произвольной координатной области решение уравненш 1я при построении характеристиче-(1.14) ищется в виде разложения по собственным векторнымской части функции Грина, связанной с осью z. При таком подфункциям [28]: ходе тензор Грина, устанавливающий связь напряженности электрического поля с электрическим током, имеет следующее пред-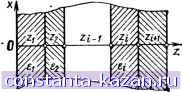

Рис. 1.1. Многослойная структура

L = V Ф, М = V X (аЩ, N = V )< V X (аХ). (1.15;Ставление:

+ ауа

где Ф, и X являются собственными функциями скалярного уравнения Гельмгольца V<p+k\=0, а вектор а в общем случае (за исключением прямоугольной системы координат) не может быть выбран произвольно. Для ортогональных цилиндрических систем обязательно выполнение условия а = а^. В [28] показано, что разложение функций G возможно как по полной системе векторных собственных функций L, М, N, так и только по поперечным функциям М и N.

В последующих параграфах воспользуемся этим разложением для нахождения тензоров Грина плоскопараллельных слоистых областей.

1.3. РАСЧЕТ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ В СЛОИСТЫХ СРЕДАХ. РАЗЛОЖЕНИЕ ПО ВОЛНАМ Е и Н

Как было отмечено выше, функция Грина может быть представлена в виде разложения по собственным поперечным векторным функциям типов М и N. Выбор поперечного сечения области t2 i и, следовательно, оси [вектор а в (1.15)], относительно которой Д^ , -е+т]

fn(r.r)=fi

1 (?-(г,г') 2

+ а,а,

dzdz dgjz, z) dzdz dgjz, z) d dz dy .

д^ ду ду

+ а,йу

dzdz

dg(z,z)

dzdz dgjz, z) dz

-f(z, z) + fiz, z)

dxdx

dxdy д

dxdy J d

dxdx dgjz, z) a dz

g{z, z)

dz dy J

(1.16)