,Cr fOCM; Its fOCy.

Проводимости пространственных волн для m-й гармоники тока имеем

/ а \2

т

y(:oasin 6) {koa sin 6)2 cos 2 6

COs2 6+(? ctgM) + [/ (Msin 6)]2X

COS 2 6

£2-)- (ej cOS6ctgSV) 1

X sin ed6. (3.61)

Проводимости поверхностных волн типов LM и LE рассчитываются по формулам:

0,05

Рис. 3.17. Проводимость нзлучрния пространственных С, и поверхностных Cs волн дисковой МПА

d/a =

I а d

(3.62)

* a

\ d } [ \o ko{kY[ koaVB\-{r4:kodf

. (3.63)

Ha рис. 3.17 приведены графики зависимости и G для дву. значений d/Ao и =2,32. Расчеты сделаны для основного типа колебаний Еио дисковой антенны. Резонансная частота

(3.64)

где

fo* 1,841 с/2т1азфКе;, 8Ф = а V1 + 2Щшг\ (In Tta/2cf + 1,7726).

Компоненты пространственной части электрического поля в дальней зоне:

£ е= cos nvfJ {koa sin 6) = sin msp

cos 6

kod У ? -f El cos 6 ctg 5*оС? ? y {koa sin6) 1 cose

sin 6 Aorf у cose-f- ctgSa

. (3.65)

Принимая BO внимание свойства функций Бесселя, отметим важное обстоятельство: только при первой азимутальной вариации тока (т=1) дисковая МПА имеем максимум излучения в направлении нормали к поверхности диска.

Из (3.65) при следуют известные формулы для диаграм-

мы направленности кольцевой щели в проводящем экране: Еь = cos <р/, {koQ sin 6); Е^ = sin J {koa sin 6)/*oa sin 6.

Проверка более строгими методами (см. 3.3.2) показала, что )езонаторный подход дает хорошие результаты при расчете вход-юго сопротивления и диаграмм направленности антенны вблизи резонанса.

3.3.2 Токовый метод. В последнее время предприняты попытки трогого подхода к решению задачи об излучении дисковой МПА 9, 74-76}. В большинстве случаев используется токовый метод, в рамках которого векторное распределение электрического тока на диске аппроксимируется тем или иным набором пробных функций. Их интегрирование с соответствующими компонентами функции Грина, записанными в цилиндрической системе координат, приводит к системе линейных алгебраических уравнений, решаемых численно. Вычисление элементов матрицы сопротивлений производится, как правило, с использованием преобразования Ханкеля 75, 76] при разбиении поверхностного тока на азимутальную и радиальную составляющие:

J (р. <р) = арУр (р, <р) + а^Уу (р, <р), (3.66)

ар, -единичные векторы в круговой цилиндрической системе координат.

Для улучшения сходимости решения и в целях экономии машинного времени при расчетах составляющие токов в (3.66) должны удовлетворять условиям на ребре: Ур {а - р)2, J::{a -

-р)-1/2.

Прежде всего в качестве пробных можно использовать системы функций волноводного типа:

J = ехр {/тп) [&fmJ (Sp)/?p + /а.У; {Щ, imi- = ехр (ут<р) [арУ„ (Sr) + уа,тУ (р)/5р1, (3.67)

где I и I -корни уравнений /т(о)=0, J (а)=0.

Системы функций (3.67) ортогональны между собой, однако для корректного описания полей вблизи кромок диска требуется слишком большое число членов ряда по номерам и корням функции Бесселя и ее производной. Значительную экономию времени при расчетах дают токовые функции вида [9]:

Л (Р) = су; (р) + в ехр [(р - a)ld] Va2-p2,

У, (р) = уСтУ (р)/5р -j- jA ехр [(р - c)/d]]/a2 - р2. (3.68)

где постоянные Л и В определяются из формул асимптотического поведения компонентов тока вблизи кромок, а С -из условия сшивания средних токов в точке р = 0.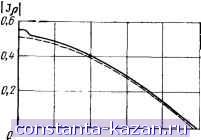

0,8 0,1 0,2

О.* 0,6 0,8 p/a 0.2 O.i ЦБ 0,8 pja

a) 6)

Рис. 3.18. Распределение радиальной (a) и азимутальной (б) составляющих электрического тока на дисковой МПА

На рис. 3.18 приведены радиальные распределения модулей составляющих токов на диске для d/fl=0,0315, е, =2,32. Сплощные кривые - с учетом 40 пробных функций типа (3.67), штриховые - для выражений (3.68) [9]. Эти результаты использованы при определении резонансной частоты и добротности дисковой антенны. На рис. 3.19 для е^=2,32 и 9,8 приведены графики нормированной резонансной частоты для основного типа колебаний. Нормировка частоты произведена к величине fo= 1,841 с/2яа lij, которая определена из условия резонанса в цилиндрическом резонаторе с магнитными стенками. Точками отмечены экспериментальные результаты при возбуждении МПА полосковой линией. Для тех же значений относительной диэлектрической проницаемости материала подложки на рис. 3.20 приведены графики зависимости добротности антенны от а\й.

Поле в дальней зоне вычисляется стандартно: компоненты токов (3.68) используются в выражении (1.11) для определения на-

fo 0,95

0,85

а

3,0 10,0 30о a/d

Рис. 3.19. Зависимость резонансной частоты МПА от соотношения радиуса диска и толщины подложки

ис 3,0 то 30.0 a/d

Рис. 3.20. Добротность дисковой МПА для двух значений диэлектрической проницаемости материала подложки

пряженности электрического поля, к которому применяется метод стационарной фазы:

е; - sin 2 е J (ka sin 6)

jVe\- sin2 6 -f e; cos 6 ctg (/ej - sin2 e kd) ~\aJ (\a)fJKa sin 6)

(W-(*o sn hJmikaasin 6)

j cos e -f /e; - sin2 e ctg (1/e; - sin2 e kd)

-mJ (Va)J {koa sin 6)

(3.69)

ila) ika) sin Ь

где \j = cos e exp [/(ф-Ь kod cos в-hnm/2)]exp {-jkoR)/R.

Эти выражения можно сравнить с (3.65), полученными в рамках резонаторного метода. На рис. 3.21,о, б приведены амплитудные ДН £е(е) и \Е^{в)\, рассчитанные по (3.65). Эти данные с графической точностью совпадают с результатами, полученными в рамках токового метода с использованием четырех пробных функций [9].

Величину Е^=0 при 6 = 90° следует отнести на счет поверхностной волны, распространяющейся в диэлектрическом слое. Приближенные методы расчета полей, не учитывающие этих волн во внешней области, дают для этого направления неверный результат [12]. Однако ввиду очень резкого спада интенсивности излучения при приближении к 6 = 90° при экспериментальных измерениях наблюдение этого провала затруднено. Кроме того, отражение волн от краев диэлектрической подложки частично заполняет этот узкий и глубокий провал в диаграмме направленности.

Здесь уместно затронуть вопрос о поляризационной характеристике дисковой МПА, функционирующей в режиме колебаний по- Сложный характер распределения тока на пластине [см. (3.66) -(3.68)] и наличие диэлектрической подложки приводят к появлению кроссполяризационной составляющей поля. Использование записей для поля в форме (3.65) или (3.69) в (3.51), (3.52) позволяет исследовать поляризационную структуру поля. Для тонких подложек (с?Ао<С1) выражение для поляризационной характеристики может быть записано в следующем виде:

г(е,<р)=

cos б sin=<pcos9y2(*o sin 6) [1 + (е^. - 1)/(е;- sin2e smy]

cos срУо(*о^81п6)+(соз2Ьз1п2 (р-cos2(p)y, {kaslu B)jkoa sin 6

Рисунок 3.22 иллюстрирует потери мощности, излученной дисковой антенной, которые связаны с образованием поверхностных волн типа LMi в слое диэлектрика в зависимости от его толщины. Потери характеризуются величиной =/?5/(/?j-j-/?r). Точками на

В, град

Ep(e)

30 60 90

В. град а)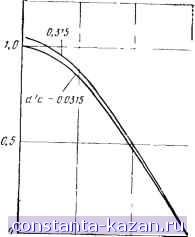

дО 60 90

в. град

90 в, град

Рис 3 21. Амплитудная диа1рамма направленности дисковой МПА в главных плоскостях для двух значений проницаемости подложки-а) е',=2,32; б) е',=9,8

графике для е| =2,32 отмечены значения а, определенные по графикам рис. 3.17, т. е. в рамках резонаторного метода. Расчеты в этом случае производились по (3.61) и (3.62).

Если принять, что антенна не должна терять более 25% излученной мощности на образование поверхностных волн, то гранич-122

Таблица 33

Число функций J, J

(2,2)

(3,3)

0 0236 0,236

0,85346 0,84478

0,97686 0,89206

0,97684 0.89143

ис. 3 22. Потери мощности на образование

оверхиостиых воли qqqj о,003 0,01 0,03 d/Tig

юй частотой для материала с ej =2,32 является величина !l/d, ГГц, и 6,9/rf, ГГц, для ej =9,8. Так, для подложки с ej = 2,32 d=l,59 мм максимально допустимой частотой является 13,2 ГГц. Как уже отмечалось, хорошие результаты для дисковой МПА логут быть получены при малом числе пробных функций, если они читывают особенность поля на кромке диска. Так, в [75] исполь-уются следующие представления для радиальной и азимутальной вставляющих тока:

Ур = р'- (а2 - р2) 2. У. = р'- ( 2 - p2)-W2, / = 1,2... (3.70)

Преобразование Ханкеля от этих функций выражается через лементарные функции, что существенно облегчает численные расчеты. В табл. 3.3 приведены расчетные значения нормированной езонансной частоты дисковой МПА, выполненной из материала с ъ\ =2,62, для случаев двух, четырех и шести пробных функций типа (3.70).

Интересно отметить, что приближенная формула для резонансной частоты основного типа колебаний (3.64) даст для d/fl= 0,0236 нормированное значение частоты 0,983, а для d/a = 0,236- 0,908, т. е. значения, более близкие к истинным значениям, чем дают расчеты с учетом двух пробных функций.

ХГополнительно к результатам, приведенным в табл. 3.3, сошлемся на графики рис. 3.23, где для трех значений е', приведены зависимости нормированных резонансных частот /о от толщины подложки.

На графиках рис. 3.24 показана зависимость ширины ДН дисковой МПА по уровню 3 дБ в плоскостях £б(де£) и Е^{1\Ьн)- Обращает на себя внимание факт стабильности ширины ДН дисковой МПА в плоскости Н при изменении толщины подложки и ее диэлектрической проницаемости.

0,8 с?7

0,05

0,5 d/a

Рис 3 23. Зависимость резонансной частоты от параметров дисковой антенны