Запишем решение для двух наиболее употребительных частных случаев, содержащих слоистый диэлектрик.

1. Волновод, частично заполненный диэлектриком (рис. 1.3). Получим разложение поперечной части функции Грина для волн типа LM:

2 2п{х, y)x:jx, у') + 2 х„, (-, у)х; (х',/)

п=\ L m=l

а

Xi,vn(. у) -

(/e*)2 = ft2 + ( / 2 + (...J,

cos \ri(xld-\-\)\

где и являются корнями системы уравнений:

Ve; COS chKa(] -xla)\

у sin (u y/6)J ,

,/-7.------ l/ sm (nylb)

где ej =ei/eo, Bj =62/60, a=afd,rl и являются v-корнями системы уравнений:

(a:)2=

г^е^ tg = e; th (a), (r)2 + (J)2 = M;

th {at) sec2 (rO с

2. = V(A:L)- + (- /&)2. Поперечная часть функции Грина для волн типа LE имеет вид:

где

/ fcosiyib)

sinlr:(x/flr+l)l

l:v (.. У) =-Л Sin rf-

/г = А;2 у^2->о. Собственные значения для первой и второй областей:

= V{n/d)-h{nib)\ = K-(W + ( /ft)-

Счетное множество функций Xvn соответствует поверхностным типам волн, которые как бы прилипают к границе раздела ди-

sh \ty{\-xid)] 2: .п (X, У) - Alhita)

COS Ыуlb)

е„=1, я = 0; е„ = 2, я=1. 2 ....

M2-f csc2(rj)-asch (<(; )

ctg(<)

Рис. 1 3 Волновод, частично заполненный диэлектриком:

/ - диэлектрик; 2 - воздух

а X

электриков. Экспоненциальный характер убывания полей при удалении от границы раздела очевиден из записи функций Хг, vn Для колебательной части спектра:

0<1<УШ, a = a/d, г* и - корни системы:

rftctgr = -icth(H {r1) + {t4) = hd<

=Y{r*jd) + {r.nibf, k\. = V-(W+(- /);

V2;m (-, Я- sin(ft5 a) LI b .

(AJ2 = l[a -f )4- (- + a)ctg2(

x, (..y)=S-

l/e;A cos(A:f flr)

Л2; mn {X, У) = -j=-

T/e;A cos (ад

j/--sin ( яу/fc) , I / -y Sin (яу/6)

*2 -корни системы:

2. Слой диэлектрика над проводящим экра (см. рис. 1.2). Разложение поперечной функции Грина для типа LM:

J- dr Х4х.у; -пЖЦх, Г; ri) +

- оо V

+ Х{х, у; ?,г,)Х*(л:.у'; k,r)d-6

(ftft)2=A:2+Y)2 (ft.ft)2.

Дискретная часть спектра:

Разложенце по волнам типа LE имеет вид:

-Ах, у, г,)Чг:(х',Г; 71) +

ном волн

Х,. (х, у; ri} =

cos \rl(xld+l)]

X,..(..v..)-j7ie-< [/J-e-.,

и являются корнями трансцендентны.х уравнений:

К. V = Vinidy + fi , (гу + {tir = hd. Функции непрерывного спектра:

Х.(х,у; S.,) = l/Ir cos.( + )

-Г2(0;5)]Х

i.v(-v, у; vi) =

sin [r>Jxld+l)]

Л? sin г'

и являются корнями уравнений:

функции непрерывного спектра:

sin L(x4-d) - Г

2 (. у; пА) = у= le- + Г2 (0; £) e--I

f /0 S+yi ctg Sifi?

1 2 (U, sj - - -

E - /?, ctg

Е2 = Л--£2,

Записанные выще функции X и легко модифицируются на? случай изменения протяженности и характера границ в направлении оси у. Для удобства замены часть собственных нормированных функций, связанных с координатой у, выделена в квадратные скобки.

Необходимо указать, что значения постоянных е, р и k, входящих в (1.24), (1.25), следует брать соответствующими области, в которой находится точка наблюдения.

Достоинством описанного подхода является то обстоятельство, что в случае открытых областей функция Грина не имеет особых точек на плоскости волновых чисел g, ц. Рещение имеет смещан-ный спектр волн, что позволяет уже на этапе рещения уравнений для поля произвести разделение волн на поверхностные и пространственные. Это, как будет показано в дальнейщем, позволит

более глубоко исследовать физические явления, происходящие и а ПОЛОСКОВЫЕ ЛИНИИ И ПОЛОСКОВЫЕ АНТЕННЫ

излучающих полосковых структурах и более полно псследоват

характеристики микрополосковых антенн. Разработка теории полосковых линий и основ их проектирования является

важным самостоятельным разделом современной прикладной электродинамики 15 ФУНКиИОНАПЫ ЭПРКТРОПИНДМИКИ семики СВЧ. Наиболее полные данные по строгому подходу к анализу

ы FH п <*ЛЬК1Р.ОДИНАтИКИ осиовных типов полосковых линий передач (ПЛП) и основам машинного про-

И ТЕНЗОРЫ ГРИНА актирования содержатся в [1]. Отметим, что знание принципов работы ПЛП

п .. вяжно для специалистов в области антенн, во-первых, для понимания принци-

В прикладной электродинамике большое значение имеют ационарньк 1 ПА и, во-вторых, построения адекватных алгоритмов их ана-функцноналы для целого ряда важных параметров, таких как: резонансная ча°° действии лил и, , р f

вГн^ост' Р^-Р-Р^н' -. поперечник рассеяния, сопротивление. про. , А вибраторного и щелевого типов физически являются отрез-воднмость и др. Стационарные выражения могут быть получены, апример П и при анализе их излучения непосредственно ис-

методом возмущении или одним из прямых вариационных методов couiBcicibtum а р . р

п , f и л mciuAvb. ПОЛЬЗУЮТ тэкис харэктеристики линии, как постоянная распространения р и

В антенных задачах исходным для определения характеристик излучение к f лдпл

лара.\1сри1.1ик пзлучкпп . .pgpjjcyjjqecKoe сопротивление Zc. Эффективность излучения МПА и ее

является интегральное уравнение для электрического тока fг) xapaкIeFи^-и'*=c i,u pv п. с ч-ч- }

lOKd J rj. согласование во многом зависят от правильного выбора линии питания. С дру-

гой стороны, следует отметить, что МПА н ПЛП имеют единые конструктив-( 26]цувд основу и технологию изготовления, однако с точки зрения эффекта нзлу-° чения решают различные задачи; ПЛП должна с минимальными потерями

где Ео - напряженность стороннего электрического поля. канализировать СВЧ мощность, а антенна должна ее эффективно излучать.

Если сравнить (1.26) с (1.11), то нетрудно убедиться, что ядром интеграль-Понимание механизма излучения электромагнитных волн полосковыми струк-ного уравнения является функция Грина (г. г') =Т (г. г'). Уравнение (1 261УР У регулировать помогает решать вопросы как ограничения после умножения на токовую функцию и интегрирование по площади антенны его стимулирования (в антеннах),

шриводит к функционалу, который имеет размерность и физический смысл вход- п^Р^хоДных цепях от МПА к приемно-передающнм устройствам испольного сопротивления антенны: г F Ф чсскии смысл вход широкий класс ПЛП. При конструировании собственно полосковых антеин чаще других применяют линии, изображенные на рнс. 1.4: экранированная ПЛ (рис. 1.4,а)-, открытая МПЛ (рис. 1.4,6); открытая МПЛ на многослойной -подложке (рис. 1.4,в); щелевая линия (рис. 1.4,г).

Z= 1 2 JJp(r).r (r.r)-P(r)5rf5.

-где / - ток на входных клеммах.

Прн использовании прямых вариационных методов, например метода Га-леркнна, в качестве токов в (1.27) выступают пробные функции, а билинейный функционал в этом случае играет роль частичного сопротивления:

Р, = .f .f J (Г t Г„ (г. г') (г') dS dS.

(1.28)

Аналогично при решении задач об излучении щелевых антенн вводится понятие частичной проводимости:

р = I .f ( )Р22 (Г, г') J (Г, Г') dSdS. (1.29)

Входное сопротивление антенны, аналогичное (12.7), можег быть получено методом наводимых ЭДС: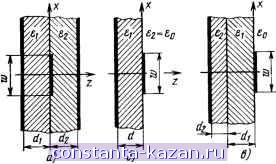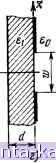

= 1/ U1 J J (г) Г„ (г. г') J- (г') dS dS. (1.30)

Если токовые функции действительны, то выражения (1.27) н (1.30) совпадают. Однако, как показано в [51], в общем случае только представление (1.27) является стационарным относительно малых вариаций тока. 26

Рис. 1.4. Полосковые линин

В полосковых структурах, изображенных на рис. 1.4, может быть использовано большое число типов гибридных волн, с продольными составляющими Е н И. Однако с точки зрения антенных приложений представляет интерес волна низшего типа - так называемая квази-7 волна. Дисперсионное уравнение для определения постоянной распространения квази-Т волны можно получить из условия отсутствия переноса энергии в поперечном направлении [46]. Это условие соответствует равенству нулю функционалов следующего вида: